No CrossRef data available.
Article contents
The epsilon constant conjecture for higher dimensional unramified twists of 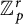 ${\mathbb Z}_p^r$(1)
${\mathbb Z}_p^r$(1)
Published online by Cambridge University Press: 29 June 2021
Abstract
Let 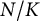 $N/K$
be a finite Galois extension of p-adic number fields, and let
$N/K$
be a finite Galois extension of p-adic number fields, and let  $\rho ^{\mathrm {nr}} \colon G_K \longrightarrow \mathrm {Gl}_r({{\mathbb Z}_{p}})$
be an r-dimensional unramified representation of the absolute Galois group
$\rho ^{\mathrm {nr}} \colon G_K \longrightarrow \mathrm {Gl}_r({{\mathbb Z}_{p}})$
be an r-dimensional unramified representation of the absolute Galois group 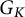 $G_K$
, which is the restriction of an unramified representation
$G_K$
, which is the restriction of an unramified representation 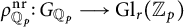 $\rho ^{\mathrm {nr}}_{{{\mathbb Q}}_{p}} \colon G_{{\mathbb Q}_{p}} \longrightarrow \mathrm {Gl}_r({{\mathbb Z}_{p}})$
. In this paper, we consider the
$\rho ^{\mathrm {nr}}_{{{\mathbb Q}}_{p}} \colon G_{{\mathbb Q}_{p}} \longrightarrow \mathrm {Gl}_r({{\mathbb Z}_{p}})$
. In this paper, we consider the 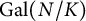 $\mathrm {Gal}(N/K)$
-equivariant local
$\mathrm {Gal}(N/K)$
-equivariant local 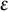 $\varepsilon $
-conjecture for the p-adic representation
$\varepsilon $
-conjecture for the p-adic representation 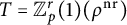 $T = \mathbb Z_p^r(1)(\rho ^{\mathrm {nr}})$
. For example, if A is an abelian variety of dimension r defined over
$T = \mathbb Z_p^r(1)(\rho ^{\mathrm {nr}})$
. For example, if A is an abelian variety of dimension r defined over 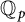 ${{\mathbb Q}_{p}}$
with good ordinary reduction, then the Tate module
${{\mathbb Q}_{p}}$
with good ordinary reduction, then the Tate module 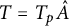 $T = T_p\hat A$
associated to the formal group
$T = T_p\hat A$
associated to the formal group 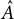 $\hat A$
of A is a p-adic representation of this form. We prove the conjecture for all tame extensions
$\hat A$
of A is a p-adic representation of this form. We prove the conjecture for all tame extensions 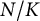 $N/K$
and a certain family of weakly and wildly ramified extensions
$N/K$
and a certain family of weakly and wildly ramified extensions 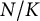 $N/K$
. This generalizes previous work of Izychev and Venjakob in the tame case and of the authors in the weakly and wildly ramified case.
$N/K$
. This generalizes previous work of Izychev and Venjakob in the tame case and of the authors in the weakly and wildly ramified case.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021



