Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T23:37:53.410Z Has data issue: false hasContentIssue false
  • English
  • Français

Entire Functions with Some Derivatives Univalent

Published online by Cambridge University Press:  20 November 2018

S. M. Shah  and
S. Y. Trimble
S. M. Shah
Affiliation:
University of Kentucky, Lexington, Kentucky
S. Y. Trimble
Affiliation:
University of Missouri, Rolla, Missouri
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is a continuation of the author's previous work, [6; 7], on the relationship between the radius of convergence of a power series and the number of derivatives of the power series which are univalent in a given disc.

In particular, let D be the open disc centered at 0, and let f be regular there. Suppose that 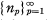is a strictly-increasing sequence of positive integers such that each f(np) is univalent in D. Let R be the radius of convergence of the power series, centered at 0, that represents f. In [7], we investigated the connection between R and 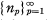. We showed that, in general

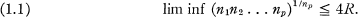
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 1 , February 1974 , pp. 207 - 213
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. FitzGerald, C. H., Exponentiation of certain quadratic inequalities for Schlicht functions, Bull. Amer. Math. Soc. 78 (1972), 209–210.Google Scholar
2. Hayman, W. K., Multivalent functions (Cambridge University Press, Cambridge, 1958).Google Scholar
3. Hobson, E. W., The theory of functions of a real variable and the theory of Fourier's series, vol. II (Dover Publications, New York, 1957).Google Scholar
4. Mitrinovic, D. S., Analytic inequalities (Springer-Verlag, New York, 1970).Google Scholar
5. Nehari, Z., Conformai mapping (McGraw-Hill, New York, 1952).Google Scholar
6. Shah, S. M. and Trimble, S. Y., Univalent functions with univalent derivatives, Bull. Amer. Math. Soc. 75 (1969), 153–157.Google Scholar
7. Shah, S. M. and Trimble, S. Y., Univalent functions with univalent derivatives, III, J. Math. Mech. 19 (1969), 451–460.Google Scholar