Article contents
The Embedding Theorems of Malcev and Lambek
Published online by Cambridge University Press: 20 November 2018
Extract
A given semigroup 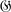 is said to be embeddable in a group if there exists a group
is said to be embeddable in a group if there exists a group 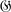 which contains a subsemigroup isomorphic to
which contains a subsemigroup isomorphic to 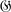 .
.
It can easily be proved that cancellation is a necessary condition for embeddability. It can also be shown that we can adjoin an identity to a semigroup without identity in such a way that the new semigroup is embeddable if and only if the original was embeddable. Therefore, we can, without loss of generality, restrict our attention to cancellation semigroups with identity, whenever this is convenient.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1963
References
- 10
- Cited by


