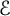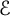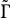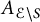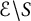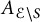1 Introduction
The hyperlogarithms (HLs) are a family of multivalued holomorphic functions on the punctured complex plane, which were first introduced in [Reference Lappo-DanilevskyLD, Reference PoincaréPo]. They are natural one-variable specializations of the family of multiple polylogarithms, which have found numerous applications in mathematics (see [Reference Bowman and BradleyBB] for a survey, as well as [Reference BrownBr]). The HLs also found applications in particle physics (see [Reference PanzerPa] and the references therein). If
![]() $S\subset \mathbb C$
is a finite subset, the HLs on
$S\subset \mathbb C$
is a finite subset, the HLs on
![]() $\mathbb C\smallsetminus S$
are defined by iterated integration of a flat connection on a trivial bundle over
$\mathbb C\smallsetminus S$
are defined by iterated integration of a flat connection on a trivial bundle over
![]() $\mathbb C\smallsetminus S$
with values in a suitable free Lie algebra ([Reference BrownBr], Section 5.1), which corresponds to a Maurer–Cartan element on
$\mathbb C\smallsetminus S$
with values in a suitable free Lie algebra ([Reference BrownBr], Section 5.1), which corresponds to a Maurer–Cartan element on
![]() $\mathbb C\smallsetminus S$
with values in this Lie algebra, and which is closely related with the KZ connection (see [Reference Enriquez and ZerbiniEZ], Remark 2.20).
$\mathbb C\smallsetminus S$
with values in this Lie algebra, and which is closely related with the KZ connection (see [Reference Enriquez and ZerbiniEZ], Remark 2.20).
Both the algebra
![]() $\mathcal H_{\mathbb C\smallsetminus S}$
generated by the HLs on
$\mathcal H_{\mathbb C\smallsetminus S}$
generated by the HLs on
![]() $\mathbb C\smallsetminus S$
and the algebra
$\mathbb C\smallsetminus S$
and the algebra
![]() ${\mathcal {O}}(\mathbb C\smallsetminus S)$
of regular functions on
${\mathcal {O}}(\mathbb C\smallsetminus S)$
of regular functions on
![]() $\mathbb C\smallsetminus S$
are subalgebras of the algebra of holomorphic multivalued functions on
$\mathbb C\smallsetminus S$
are subalgebras of the algebra of holomorphic multivalued functions on
![]() $\mathbb C\smallsetminus S$
. Their product
$\mathbb C\smallsetminus S$
. Their product
![]() $\mathcal H_{\mathbb C\smallsetminus S}\cdot {\mathcal {O}}(\mathbb C\smallsetminus S)$
within this algebra is stable under the operators
$\mathcal H_{\mathbb C\smallsetminus S}\cdot {\mathcal {O}}(\mathbb C\smallsetminus S)$
within this algebra is stable under the operators
![]() $\mathrm {int}_\omega : f\mapsto (z\mapsto \int _{z_0}^z f\omega )$
for
$\mathrm {int}_\omega : f\mapsto (z\mapsto \int _{z_0}^z f\omega )$
for
![]() $\omega $
in the space
$\omega $
in the space
![]() $\Omega (\mathbb C\smallsetminus S)$
of regular differentials on
$\Omega (\mathbb C\smallsetminus S)$
of regular differentials on
![]() $\mathbb C\smallsetminus S$
, where
$\mathbb C\smallsetminus S$
, where
![]() $z_0$
is a fixed point of
$z_0$
is a fixed point of
![]() $\mathbb C\smallsetminus S$
([Reference BrownBr], Cor 5.6), and it coincides with the minimal algebra with these properties
$\mathbb C\smallsetminus S$
([Reference BrownBr], Cor 5.6), and it coincides with the minimal algebra with these properties
![]() $A_{\mathbb C\smallsetminus S}$
(see [Reference Enriquez and ZerbiniEZ], Theorem A). It is proven in [Reference BrownBr], Section 5.2, that
$A_{\mathbb C\smallsetminus S}$
(see [Reference Enriquez and ZerbiniEZ], Theorem A). It is proven in [Reference BrownBr], Section 5.2, that
![]() $\mathcal H_{\mathbb C\smallsetminus S}\cdot {\mathcal {O}}(\mathbb C\smallsetminus S)$
is isomorphic to
$\mathcal H_{\mathbb C\smallsetminus S}\cdot {\mathcal {O}}(\mathbb C\smallsetminus S)$
is isomorphic to
![]() ${\mathcal {O}}(\mathbb C\smallsetminus S)\otimes \mathcal H_{\mathbb C\smallsetminus S}$
, and that
${\mathcal {O}}(\mathbb C\smallsetminus S)\otimes \mathcal H_{\mathbb C\smallsetminus S}$
, and that
![]() $\mathcal H_{\mathbb C\smallsetminus S}$
is isomorphic to an explicit shuffle algebra; this enables to prove that this product is a free module over
$\mathcal H_{\mathbb C\smallsetminus S}$
is isomorphic to an explicit shuffle algebra; this enables to prove that this product is a free module over
![]() ${\mathcal{O}}(\mathbb C\smallsetminus S)$
, and that a basis is given by the HLs (see [Reference BrownBr] Corollary 5.6, and also [Reference Deneufchâtel, Duchamp, Minh, Solomon and WinklerDDMS]).
${\mathcal{O}}(\mathbb C\smallsetminus S)$
, and that a basis is given by the HLs (see [Reference BrownBr] Corollary 5.6, and also [Reference Deneufchâtel, Duchamp, Minh, Solomon and WinklerDDMS]).
When
![]() $\mathbb C\smallsetminus S$
is replaced by an arbitrary affine curve C, one can similarly attach to any Maurer–Cartan element J, non-degenerate in the sense of [Reference Enriquez and ZerbiniEZ], an algebra
$\mathbb C\smallsetminus S$
is replaced by an arbitrary affine curve C, one can similarly attach to any Maurer–Cartan element J, non-degenerate in the sense of [Reference Enriquez and ZerbiniEZ], an algebra
![]() $\mathcal H_C(J)$
of multivalued holomorphic functions on C (see [Reference Enriquez and ZerbiniEZ], Section 2.3). The above result for the punctured complex plane extends to this case, namely the product of the algebra
$\mathcal H_C(J)$
of multivalued holomorphic functions on C (see [Reference Enriquez and ZerbiniEZ], Section 2.3). The above result for the punctured complex plane extends to this case, namely the product of the algebra
![]() $\mathcal H_C(J)$
with the algebra
$\mathcal H_C(J)$
with the algebra
![]() ${\mathcal {O}}(C)$
of regular functions on C coincides with the minimal subalgebra
${\mathcal {O}}(C)$
of regular functions on C coincides with the minimal subalgebra
![]() $A_C$
of the algebra of multivalued functions on C that is stable under the analogs
$A_C$
of the algebra of multivalued functions on C that is stable under the analogs
![]() $\mathrm {int}_\omega $
of the above operators, where
$\mathrm {int}_\omega $
of the above operators, where
![]() $\omega $
runs over the space
$\omega $
runs over the space
![]() $\Omega (C)$
of regular differentials on C ([Reference Enriquez and ZerbiniEZ], Theorem A(b)), and is therefore independent of J. The algebra
$\Omega (C)$
of regular differentials on C ([Reference Enriquez and ZerbiniEZ], Theorem A(b)), and is therefore independent of J. The algebra
![]() $A_C$
can also be characterised as the set of multivalued holomorphic functions on C which have moderate growth at the cusps of C and have unipotent monodromy, in the sense that the representation of the fundamental group of C generated by such a function is a finite iterated extension of the trivial representation ([Reference Enriquez and ZerbiniEZ], Theorem C). In [Reference Enriquez and ZerbiniEZ], Theorem A(b), one shows the isomorphisms of
$A_C$
can also be characterised as the set of multivalued holomorphic functions on C which have moderate growth at the cusps of C and have unipotent monodromy, in the sense that the representation of the fundamental group of C generated by such a function is a finite iterated extension of the trivial representation ([Reference Enriquez and ZerbiniEZ], Theorem C). In [Reference Enriquez and ZerbiniEZ], Theorem A(b), one shows the isomorphisms of
![]() $A_C$
with
$A_C$
with
![]() ${\mathcal {O}}(C) \otimes \mathcal H_C(J)$
and of
${\mathcal {O}}(C) \otimes \mathcal H_C(J)$
and of
![]() $\mathcal H_C(J)$
with an explicit shuffle algebra; this enables us to attach to a family of
$\mathcal H_C(J)$
with an explicit shuffle algebra; this enables us to attach to a family of
![]() $\Omega (C)$
, whose image is a basis of
$\Omega (C)$
, whose image is a basis of
![]() $\Omega (C)/d{\mathcal {O}}(C)$
, a basis of
$\Omega (C)/d{\mathcal {O}}(C)$
, a basis of
![]() $A_C$
as an
$A_C$
as an
![]() ${\mathcal {O}}(C)$
-module (Definition 2.6 and Lemams 2.5 and 2.7), whose elements are analogs of the classical HLs.
${\mathcal {O}}(C)$
-module (Definition 2.6 and Lemams 2.5 and 2.7), whose elements are analogs of the classical HLs.
In this article, we will be interested in the particular case where C has genus one; more precisely, we take it to coincide with the affine curve
![]() ${\mathcal {E}}_S:={\mathcal {E}}\smallsetminus S$
, for
${\mathcal {E}}_S:={\mathcal {E}}\smallsetminus S$
, for
![]() ${\mathcal {E}}$
a complex elliptic curve and
${\mathcal {E}}$
a complex elliptic curve and
![]() $S\subset {\mathcal {E}}$
a finite non-empty subset. In §2.5, we exhibit an explicit family of
$S\subset {\mathcal {E}}$
a finite non-empty subset. In §2.5, we exhibit an explicit family of
![]() $\Omega ({\mathcal {E}}_S)$
whose image is a basis of
$\Omega ({\mathcal {E}}_S)$
whose image is a basis of
![]() $\Omega ({\mathcal {E}}_S)/d{\mathcal {O}}({\mathcal {E}}_S)$
; according to Lemmas 2.5 and 2.7, this gives rise to a basis of
$\Omega ({\mathcal {E}}_S)/d{\mathcal {O}}({\mathcal {E}}_S)$
; according to Lemmas 2.5 and 2.7, this gives rise to a basis of
![]() $A_{{\mathcal {E}}_S}$
as an
$A_{{\mathcal {E}}_S}$
as an
![]() ${\mathcal {O}}({\mathcal {E}}_S)$
-module, whose elements will be called elliptic hyperlogarithms.
${\mathcal {O}}({\mathcal {E}}_S)$
-module, whose elements will be called elliptic hyperlogarithms.
Recent development in particle physics led to the introduction of two (closely related) classes of multivalued functions
![]() $\tilde \Gamma $
and
$\tilde \Gamma $
and
![]() $\mathrm E_3$
on
$\mathrm E_3$
on
![]() ${\mathcal {E}}_S$
(see [Reference Broedel, Duhr, Dulat and TancrediBDDT], and [Reference Broedel and KaderliBK, Reference Broedel, Mafra, Matthes and SchlottererBMMS] for applications in string theory). The functions
${\mathcal {E}}_S$
(see [Reference Broedel, Duhr, Dulat and TancrediBDDT], and [Reference Broedel and KaderliBK, Reference Broedel, Mafra, Matthes and SchlottererBMMS] for applications in string theory). The functions
![]() $\tilde \Gamma $
are defined as iterated integrals of multivalued holomorphic differential forms on
$\tilde \Gamma $
are defined as iterated integrals of multivalued holomorphic differential forms on
![]() $\mathbb C\smallsetminus pr^{-1}(S)$
,
$\mathbb C\smallsetminus pr^{-1}(S)$
,
![]() $pr : \mathbb C\to {\mathcal {E}}$
being a universal covering map. One can show that the functions
$pr : \mathbb C\to {\mathcal {E}}$
being a universal covering map. One can show that the functions
![]() $\tilde \Gamma $
may also be defined, using iterated integration, out of a holomorphic flat connection on a non-trivial bundle over
$\tilde \Gamma $
may also be defined, using iterated integration, out of a holomorphic flat connection on a non-trivial bundle over
![]() ${\mathcal {E}}_S$
, which can be identified with a connection obtained upon restriction from the “universal KZB” connection of [Reference Calaque, Enriquez and EtingofCEE] (or [Reference Levin and RacinetLR] if
${\mathcal {E}}_S$
, which can be identified with a connection obtained upon restriction from the “universal KZB” connection of [Reference Calaque, Enriquez and EtingofCEE] (or [Reference Levin and RacinetLR] if
![]() $|S|=1$
).
$|S|=1$
).
The main result of this article is a proof that the collection of functions
![]() $\tilde \Gamma $
gives rise to a basis of
$\tilde \Gamma $
gives rise to a basis of
![]() $A_{{\mathcal {E}}_S}$
over
$A_{{\mathcal {E}}_S}$
over
![]() ${\mathcal {O}}({\mathcal {E}}_S)$
(see Theorem 4.27), alternative to the family of elliptic HLs from §2.5. This relies on two main steps:
${\mathcal {O}}({\mathcal {E}}_S)$
(see Theorem 4.27), alternative to the family of elliptic HLs from §2.5. This relies on two main steps:
-
(a) We prove that
 $A_{{\mathcal {E}}_S}$
is equal to an algebra
$A_{{\mathcal {E}}_S}$
is equal to an algebra
 $\mathcal G$
generated by the functions
$\mathcal G$
generated by the functions
 $\tilde \Gamma $
(Theorem 4.20): the inclusion
$\tilde \Gamma $
(Theorem 4.20): the inclusion
 $\mathcal G \subset A_{{\mathcal {E}}_S}$
(Corollary 4.4) is based on the characterization of
$\mathcal G \subset A_{{\mathcal {E}}_S}$
(Corollary 4.4) is based on the characterization of
 $A_{{\mathcal {E}}_S}$
as the set of multivalued functions sharing certain differential properties, and the inclusion
$A_{{\mathcal {E}}_S}$
as the set of multivalued functions sharing certain differential properties, and the inclusion
 $\mathcal G \supset A_{{\mathcal {E}}_S}$
is based on the characterization of
$\mathcal G \supset A_{{\mathcal {E}}_S}$
is based on the characterization of
 $A_{{\mathcal {E}}_S}$
as the minimal algebra of multivalued functions which are stable under the endomorphisms
$A_{{\mathcal {E}}_S}$
as the minimal algebra of multivalued functions which are stable under the endomorphisms
 $\mathrm {int}_\omega $
(see Theorem 4.20).
$\mathrm {int}_\omega $
(see Theorem 4.20). -
(b) We prove a linear independence result for the functions
 $\tilde \Gamma $
(see Proposition 4.26), based on a criterion of [Reference Deneufchâtel, Duchamp, Minh, Solomon and WinklerDDMS] and on a precise analysis of differential algebras attached to
$\tilde \Gamma $
(see Proposition 4.26), based on a criterion of [Reference Deneufchâtel, Duchamp, Minh, Solomon and WinklerDDMS] and on a precise analysis of differential algebras attached to
 ${\mathcal {E}}_S$
.
${\mathcal {E}}_S$
.
The definition of the functions
![]() $\mathrm E_3$
relies on the additional datum of a degree 2 covering map
$\mathrm E_3$
relies on the additional datum of a degree 2 covering map
![]() $\pi :{\mathcal {E}}\to \mathbb P^1_{\mathbb C}$
and a finite subset
$\pi :{\mathcal {E}}\to \mathbb P^1_{\mathbb C}$
and a finite subset
![]() $S_0\subset \mathbb P^1_{\mathbb C}$
. It is shown in [Reference Broedel, Duhr, Dulat and TancrediBDDT], §5 (see also Proposition 5.4 in this paper) that the vector spaces of multivalued functions generated by the
$S_0\subset \mathbb P^1_{\mathbb C}$
. It is shown in [Reference Broedel, Duhr, Dulat and TancrediBDDT], §5 (see also Proposition 5.4 in this paper) that the vector spaces of multivalued functions generated by the
![]() $\tilde \Gamma $
and by the
$\tilde \Gamma $
and by the
![]() $\mathrm E_3$
coincide if
$\mathrm E_3$
coincide if
![]() $S=\pi ^{-1}(S_0)$
. In [Reference Broedel, Duhr, Dulat and TancrediBDDT] it also shown that an algebra constructed out of the functions
$S=\pi ^{-1}(S_0)$
. In [Reference Broedel, Duhr, Dulat and TancrediBDDT] it also shown that an algebra constructed out of the functions
![]() $\mathrm E_3$
is stable under integration (Section 6, based on explicit computation). A consequence of (a) is an alternative proof of this stability result (see Proposition 5.6).
$\mathrm E_3$
is stable under integration (Section 6, based on explicit computation). A consequence of (a) is an alternative proof of this stability result (see Proposition 5.6).
1.1 History and outlook
The first appearance of elliptic analogs of hyperlogarithms dates back to [Reference Brown and LevinBL], Section 10.1, where the authors construct functions called “elliptic Debye hyperlogarithm” via averaging of classical polylogarithm functions, generalizing analogous constructions of [Reference BlochBl, Reference LevinLe, Reference ZagierZ1]. These functions are holomorphic and multivalued, and we expect them to be contained in the algebra
![]() $A_{{\mathcal {E}}_S}$
(work in progress). They are closely related (see [Reference Brown and LevinBL], Section 10.3) to certain real-analytic functions defined via iterated integration out of a real-analytic version of the KZB connection of [Reference Calaque, Enriquez and EtingofCEE]; such functions may be seen as real-analytic analogs of elliptic hyperlogarithms, and were recently generalized to higher-genus Riemann surfaces in [Reference D’Hoker, Hidding and SchlottererDHS].
$A_{{\mathcal {E}}_S}$
(work in progress). They are closely related (see [Reference Brown and LevinBL], Section 10.3) to certain real-analytic functions defined via iterated integration out of a real-analytic version of the KZB connection of [Reference Calaque, Enriquez and EtingofCEE]; such functions may be seen as real-analytic analogs of elliptic hyperlogarithms, and were recently generalized to higher-genus Riemann surfaces in [Reference D’Hoker, Hidding and SchlottererDHS].
1.2 Organisation of the article
In Section 2, we recall from [Reference Enriquez and ZerbiniEZ] the construction and properties of the algebra
![]() $A_C$
attached to a curve C, and we specialize these results to the situation of an elliptic curve; in particular, we exhibit a basis of
$A_C$
attached to a curve C, and we specialize these results to the situation of an elliptic curve; in particular, we exhibit a basis of
![]() $A_{{\mathcal {E}}_S}$
over
$A_{{\mathcal {E}}_S}$
over
![]() ${\mathcal {O}}({\mathcal {E}}_S)$
which consists of elliptic HLs (§2.5). We then recall in Section 3 the definition of the functions
${\mathcal {O}}({\mathcal {E}}_S)$
which consists of elliptic HLs (§2.5). We then recall in Section 3 the definition of the functions
![]() $\tilde \Gamma $
([Reference Broedel, Duhr, Dulat and TancrediBDDT]), paying special attention to regularization issues. Section 4 is devoted to proving our main result: the family of functions
$\tilde \Gamma $
([Reference Broedel, Duhr, Dulat and TancrediBDDT]), paying special attention to regularization issues. Section 4 is devoted to proving our main result: the family of functions
![]() $\tilde \Gamma $
gives rise to a basis of
$\tilde \Gamma $
gives rise to a basis of
![]() $A_{{\mathcal {E}}_S}$
over
$A_{{\mathcal {E}}_S}$
over
![]() ${\mathcal {O}}({\mathcal {E}}_S)$
(Theorem 4.27), alternative to the basis from Section 2.5. In Section 5, we apply results from Section 4 to deduce a new proof of a result of [Reference Broedel, Duhr, Dulat and TancrediBDDT] on the stability under integration of an algebra
${\mathcal {O}}({\mathcal {E}}_S)$
(Theorem 4.27), alternative to the basis from Section 2.5. In Section 5, we apply results from Section 4 to deduce a new proof of a result of [Reference Broedel, Duhr, Dulat and TancrediBDDT] on the stability under integration of an algebra
![]() $\mathcal A_3$
constructed out of the functions
$\mathcal A_3$
constructed out of the functions
![]() $\mathrm E_3$
.
$\mathrm E_3$
.
1.3 Conventions, notation
In this paper, all vector spaces and algebras will be understood to be with base field
![]() $\mathbb C$
.
$\mathbb C$
.
1.3.1 Filtrations
A filtered vector space
![]() $F_\bullet V$
is the data of a vector space V and a collection of subspaces
$F_\bullet V$
is the data of a vector space V and a collection of subspaces
![]() $(F_nV)_{n\geq 0}$
such that
$(F_nV)_{n\geq 0}$
such that
![]() $F_nV\subset F_{n+1}V$
for any
$F_nV\subset F_{n+1}V$
for any
![]() $n\geq 0$
; by convention,
$n\geq 0$
; by convention,
![]() $F_{-1}V=0$
. A morphism of filtered vector spaces
$F_{-1}V=0$
. A morphism of filtered vector spaces
![]() $F_\bullet V\to F_\bullet W$
is a linear map
$F_\bullet V\to F_\bullet W$
is a linear map
![]() $f : V\to W$
, such that
$f : V\to W$
, such that
![]() $f(F_nV)\subset F_nW$
for any
$f(F_nV)\subset F_nW$
for any
![]() $n\geq 0$
. The associated graded of the filtered vector space
$n\geq 0$
. The associated graded of the filtered vector space
![]() $F_\bullet V$
is the graded vector space
$F_\bullet V$
is the graded vector space
![]() $\mathrm {gr}(V):=\oplus _{n\geq 0}\mathrm {gr}_n(V)$
, where
$\mathrm {gr}(V):=\oplus _{n\geq 0}\mathrm {gr}_n(V)$
, where
![]() $\mathrm {gr}_n(V):=F_nV/F_{n-1}V$
. If
$\mathrm {gr}_n(V):=F_nV/F_{n-1}V$
. If
![]() $F_\bullet V$
is a filtration of a vector space V, we denote by
$F_\bullet V$
is a filtration of a vector space V, we denote by
![]() $x\mapsto \overline x$
the projection map
$x\mapsto \overline x$
the projection map
![]() $F_nV\to \mathrm {gr}_n(V)$
for any
$F_nV\to \mathrm {gr}_n(V)$
for any
![]() $n\geq 0$
. If
$n\geq 0$
. If
![]() $F_\bullet V$
and
$F_\bullet V$
and
![]() $F_\bullet W$
are filtered vector spaces, their tensor product
$F_\bullet W$
are filtered vector spaces, their tensor product
![]() $F_\bullet (V\otimes W)$
is the data of
$F_\bullet (V\otimes W)$
is the data of
![]() $V\otimes W$
, equipped with the filtration given by
$V\otimes W$
, equipped with the filtration given by
![]() $F_n(V\otimes W):=\sum _{p=0}^n F_pV\otimes F_{n-p}W$
. A filtered algebra is an algebra A equipped with a filtration
$F_n(V\otimes W):=\sum _{p=0}^n F_pV\otimes F_{n-p}W$
. A filtered algebra is an algebra A equipped with a filtration
![]() $F_\bullet A$
, such that the product of A is a morphism of filtered vector spaces
$F_\bullet A$
, such that the product of A is a morphism of filtered vector spaces
![]() $F_\bullet (A\otimes A) \to F_\bullet A$
.
$F_\bullet (A\otimes A) \to F_\bullet A$
.
The total space of a filtered vector space
![]() $F_\bullet V$
is the subspace
$F_\bullet V$
is the subspace
![]() $F_\infty V:=\cup _{n\geq 0}F_nV$
of V. The total space
$F_\infty V:=\cup _{n\geq 0}F_nV$
of V. The total space
![]() $F_\infty A$
of a filtered algebra
$F_\infty A$
of a filtered algebra
![]() $F_\bullet A$
is then a subalgebra of A.
$F_\bullet A$
is then a subalgebra of A.
1.3.2 Meromorphic functions
For
![]() $\Sigma \subset \mathbb C$
a discrete subset, let
$\Sigma \subset \mathbb C$
a discrete subset, let
![]() ${\mathcal {O}}_{mer}(\mathbb C,\Sigma )$
be the algebra of meromorphic functions on
${\mathcal {O}}_{mer}(\mathbb C,\Sigma )$
be the algebra of meromorphic functions on
![]() $\mathbb C$
with sets of poles contained in
$\mathbb C$
with sets of poles contained in
![]() $\Sigma $
. It is contained in the algebra
$\Sigma $
. It is contained in the algebra
![]() ${\mathcal {O}}_{hol}(\mathbb C\smallsetminus \Sigma )$
of holomorphic functions on
${\mathcal {O}}_{hol}(\mathbb C\smallsetminus \Sigma )$
of holomorphic functions on
![]() $\mathbb C\smallsetminus \Sigma $
, and it is equipped with a derivation
$\mathbb C\smallsetminus \Sigma $
, and it is equipped with a derivation
![]() $\partial :=\partial /\partial z$
; we use the notation
$\partial :=\partial /\partial z$
; we use the notation
![]() $f':=\partial (f)$
. For
$f':=\partial (f)$
. For
![]() $a\in \mathbb C$
, we denote by
$a\in \mathbb C$
, we denote by
![]() $T_a$
the automorphism of the algebra of meromorphic functions on
$T_a$
the automorphism of the algebra of meromorphic functions on
![]() $\mathbb C$
(equal to
$\mathbb C$
(equal to
![]() $\cup _\Sigma {\mathcal {O}}_{mer}(\mathbb C,\Sigma )$
) defined by
$\cup _\Sigma {\mathcal {O}}_{mer}(\mathbb C,\Sigma )$
) defined by
![]() $T_af:=(z\mapsto f(z-a))$
.
$T_af:=(z\mapsto f(z-a))$
.
2 Minimal stable subalgebras and elliptic hyperlogarithms (based on [Reference Enriquez and ZerbiniEZ])
In §§2.1–2.3, we recall material from [Reference Enriquez and ZerbiniEZ]. More precisely, to each smooth affine complex curve C, we attach a subalgebra
![]() $A_C$
of the algebra of holomorphic functions
$A_C$
of the algebra of holomorphic functions
![]() ${\mathcal {O}}_{hol}(\tilde C)$
on a universal cover of C (see Lem-Definition 2.2), called the minimal stable subalgebra (Section 2.1); we define an algebra filtration
${\mathcal {O}}_{hol}(\tilde C)$
on a universal cover of C (see Lem-Definition 2.2), called the minimal stable subalgebra (Section 2.1); we define an algebra filtration
![]() $F_\bullet ^\delta {\mathcal {O}}_{hol}(\tilde C)$
of
$F_\bullet ^\delta {\mathcal {O}}_{hol}(\tilde C)$
of
![]() ${\mathcal {O}}_{hol}(\tilde C)$
with
${\mathcal {O}}_{hol}(\tilde C)$
with
![]() $A_C=F_\infty ^\delta {\mathcal {O}}_{hol}(\tilde C)$
(see Theorem 2.3(b)) (see Section 2.2); we express an
$A_C=F_\infty ^\delta {\mathcal {O}}_{hol}(\tilde C)$
(see Theorem 2.3(b)) (see Section 2.2); we express an
![]() ${\mathcal {O}}(C)$
-basis of
${\mathcal {O}}(C)$
-basis of
![]() $A_C$
in terms of HL functions associated with C (Section 2.3). In §2.4, we introduce the elliptic setup needed for the main results of the paper; then
$A_C$
in terms of HL functions associated with C (Section 2.3). In §2.4, we introduce the elliptic setup needed for the main results of the paper; then
![]() $C={\mathcal {E}}_S$
. In §2.5, we formulate a result of [Reference Enriquez and ZerbiniEZ] in the elliptic context, namely the expression of a
$C={\mathcal {E}}_S$
. In §2.5, we formulate a result of [Reference Enriquez and ZerbiniEZ] in the elliptic context, namely the expression of a
![]() ${\mathcal {O}}({\mathcal {E}}_S)$
-basis of
${\mathcal {O}}({\mathcal {E}}_S)$
-basis of
![]() $A_{{\mathcal {E}}_S}$
in terms of elliptic HL functions.
$A_{{\mathcal {E}}_S}$
in terms of elliptic HL functions.
2.1 The minimal stable subalgebra
 $A_C$
associated with a curve C
$A_C$
associated with a curve C
Let C be a smooth affine complex curve, which we view as a Riemann surface. Let us fix a universal cover
![]() $p:\tilde C\to C$
and let
$p:\tilde C\to C$
and let
![]() ${\mathcal {O}}_{hol}(\tilde C)$
be the algebra of holomorphic functions on
${\mathcal {O}}_{hol}(\tilde C)$
be the algebra of holomorphic functions on
![]() $\tilde C$
.
$\tilde C$
.
Let
![]() $\Omega (C)$
be the space of regular differentials on C. For any
$\Omega (C)$
be the space of regular differentials on C. For any
![]() $\omega \in \Omega (C)$
, the map
$\omega \in \Omega (C)$
, the map
![]() $f\mapsto f\cdot p^*(\omega )$
is a linear map
$f\mapsto f\cdot p^*(\omega )$
is a linear map
![]() ${\mathcal {O}}_{hol}(\tilde C)\to \Omega _{hol}(\tilde C)$
, where
${\mathcal {O}}_{hol}(\tilde C)\to \Omega _{hol}(\tilde C)$
, where
![]() $\Omega _{hol}(V)$
is the space of holomorphic differential 1-forms on a complex manifold V. For any
$\Omega _{hol}(V)$
is the space of holomorphic differential 1-forms on a complex manifold V. For any
![]() $z_0\in \tilde C$
and any
$z_0\in \tilde C$
and any
![]() $\alpha \in \Omega _{hol}(\tilde C)$
, the assignment
$\alpha \in \Omega _{hol}(\tilde C)$
, the assignment
![]() $\alpha \mapsto [z\mapsto \int _{z_0}^z \alpha ]$
is well-defined as
$\alpha \mapsto [z\mapsto \int _{z_0}^z \alpha ]$
is well-defined as
![]() $\tilde C$
is simply-connected, and defines a linear map
$\tilde C$
is simply-connected, and defines a linear map
![]() $\Omega _{hol}(\tilde C)\to {\mathcal {O}}_{hol}(\tilde C)$
. For
$\Omega _{hol}(\tilde C)\to {\mathcal {O}}_{hol}(\tilde C)$
. For
![]() $\omega \in \Omega (C)$
, let
$\omega \in \Omega (C)$
, let
![]() $\mathrm {int}_{\omega }$
be the linear endomorphism of
$\mathrm {int}_{\omega }$
be the linear endomorphism of
![]() ${\mathcal {O}}_{hol}(\tilde C)$
given by
${\mathcal {O}}_{hol}(\tilde C)$
given by
![]() $f\mapsto [z\mapsto \int _{z_0}^z f\cdot p^*(\omega )]$
.
$f\mapsto [z\mapsto \int _{z_0}^z f\cdot p^*(\omega )]$
.
Definition 2.1 A stable subalgebra of
![]() ${\mathcal {O}}_{hol}(\tilde C)$
is a subalgebra with unit, which is stable under the endomorphism
${\mathcal {O}}_{hol}(\tilde C)$
is a subalgebra with unit, which is stable under the endomorphism
![]() $\mathrm {int}_\omega $
for any
$\mathrm {int}_\omega $
for any
![]() $\omega \in \Omega (C)$
.
$\omega \in \Omega (C)$
.
Although the definition of the operators
![]() $\mathrm {int}_{\omega }$
depends on a choice of
$\mathrm {int}_{\omega }$
depends on a choice of
![]() $z_0$
, one checks that the notion of stable subalgebra is independent of such a choice.
$z_0$
, one checks that the notion of stable subalgebra is independent of such a choice.
Lemma-Definition 2.2 (see [Reference Enriquez and ZerbiniEZ], Section 5.3)
If
![]() $A_C:=\cap _{A\mathrm {\ stable\ subalgebra\ of\ }{\mathcal {O}}_{hol}(\tilde C)}A$
, then
$A_C:=\cap _{A\mathrm {\ stable\ subalgebra\ of\ }{\mathcal {O}}_{hol}(\tilde C)}A$
, then
![]() $A_C$
is a stable subalgebra of
$A_C$
is a stable subalgebra of
![]() ${\mathcal {O}}_{hol}(\tilde C)$
, which is minimal for the inclusion; it is called the minimal stable subalgebra of
${\mathcal {O}}_{hol}(\tilde C)$
, which is minimal for the inclusion; it is called the minimal stable subalgebra of
![]() ${\mathcal {O}}_{hol}(\tilde C)$
.
${\mathcal {O}}_{hol}(\tilde C)$
.
2.2 Relation of
 $A_C$
with the differential filtration
$A_C$
with the differential filtration
Define inductively a collection of subspaces
![]() $(F^\delta _n{\mathcal {O}}_{hol}(\tilde C))_{n\geq 0}$
of
$(F^\delta _n{\mathcal {O}}_{hol}(\tilde C))_{n\geq 0}$
of
![]() ${\mathcal {O}}_{hol}(\tilde C)$
by
${\mathcal {O}}_{hol}(\tilde C)$
by
![]() $F^\delta _0{\mathcal {O}}_{hol}(\tilde C):=\mathbb C$
, and
$F^\delta _0{\mathcal {O}}_{hol}(\tilde C):=\mathbb C$
, and
![]() $F^\delta _{n+1}{\mathcal {O}}_{hol}(\tilde C):=\{f\in \mathcal O_{hol}(\tilde C)\,|\,df\in F^\delta _n\mathcal O_{hol}(\tilde C)\cdot p^*\Omega (C)\}$
for
$F^\delta _{n+1}{\mathcal {O}}_{hol}(\tilde C):=\{f\in \mathcal O_{hol}(\tilde C)\,|\,df\in F^\delta _n\mathcal O_{hol}(\tilde C)\cdot p^*\Omega (C)\}$
for
![]() $n\geq 0$
. Define also the subspace
$n\geq 0$
. Define also the subspace
![]() $F^\delta _\infty {\mathcal {O}}_{hol}(\tilde C):=\cup _{n\geq 0}F^\delta _n{\mathcal {O}}_{hol}(\tilde C)$
of
$F^\delta _\infty {\mathcal {O}}_{hol}(\tilde C):=\cup _{n\geq 0}F^\delta _n{\mathcal {O}}_{hol}(\tilde C)$
of
![]() ${\mathcal {O}}_{hol}(\tilde C)$
.
${\mathcal {O}}_{hol}(\tilde C)$
.
Let us denote by
![]() ${\mathcal {O}}(C)$
the algebra of regular functions on C.
${\mathcal {O}}(C)$
the algebra of regular functions on C.
Theorem 2.3 (see [Reference Enriquez and ZerbiniEZ])
(a)
![]() $F^\delta _\bullet {\mathcal {O}}_{hol}(\tilde C)$
is an algebra filtration of
$F^\delta _\bullet {\mathcal {O}}_{hol}(\tilde C)$
is an algebra filtration of
![]() ${\mathcal {O}}_{hol}(\tilde C)$
, such that
${\mathcal {O}}_{hol}(\tilde C)$
, such that
![]() $p^*{\mathcal {O}}(C)\subset F^\delta _1{\mathcal {O}}_{hol}(\tilde C)$
.
$p^*{\mathcal {O}}(C)\subset F^\delta _1{\mathcal {O}}_{hol}(\tilde C)$
.
(b)
![]() $F^\delta _\infty {\mathcal {O}}_{hol}(\tilde C)=A_C$
.
$F^\delta _\infty {\mathcal {O}}_{hol}(\tilde C)=A_C$
.
Proof The fact that
![]() $F^\delta _\bullet $
is an algebra filtration is proven in [Reference Enriquez and ZerbiniEZ], Prop 5.5(a). The inclusion
$F^\delta _\bullet $
is an algebra filtration is proven in [Reference Enriquez and ZerbiniEZ], Prop 5.5(a). The inclusion
![]() $p^*{\mathcal {O}}(C)\subset F^\delta _1\mathcal O_{hol}(\tilde C)$
follows from the
$p^*{\mathcal {O}}(C)\subset F^\delta _1\mathcal O_{hol}(\tilde C)$
follows from the
![]() $n=0$
case of Prop 5.5(b) in [Reference Enriquez and ZerbiniEZ]. Statement (b) follows from [Reference Enriquez and ZerbiniEZ], Theorem C.
$n=0$
case of Prop 5.5(b) in [Reference Enriquez and ZerbiniEZ]. Statement (b) follows from [Reference Enriquez and ZerbiniEZ], Theorem C.
2.3 Analogs of HLs on a curve C
For W a complex vector space, denote by
![]() $\mathrm {Sh}(W)$
the shuffle Hopf algebra of W. This is the vector space
$\mathrm {Sh}(W)$
the shuffle Hopf algebra of W. This is the vector space
![]() $\oplus _{k\geq 0}W^{\otimes k}$
(the element
$\oplus _{k\geq 0}W^{\otimes k}$
(the element
![]() $w_1\otimes \cdots \otimes w_k\in W^{\otimes k}$
is denoted
$w_1\otimes \cdots \otimes w_k\in W^{\otimes k}$
is denoted
![]() $[w_1|\cdots |w_k]$
), equipped with the shuffle product
$[w_1|\cdots |w_k]$
), equipped with the shuffle product ![]() , which is commutative, the deconcatenation coproduct
, which is commutative, the deconcatenation coproduct
![]() $\Delta $
given by
$\Delta $
given by
![]() $[w_1|\cdots |w_k]\mapsto \sum _{j=0}^k[w_1|\ldots |w_j]\otimes [w_{j+1}|\ldots |w_k]$
, the counit
$[w_1|\cdots |w_k]\mapsto \sum _{j=0}^k[w_1|\ldots |w_j]\otimes [w_{j+1}|\ldots |w_k]$
, the counit
![]() $\varepsilon $
given by
$\varepsilon $
given by
![]() $1\mapsto 1$
and
$1\mapsto 1$
and
![]() $[w_1|\cdots |w_k]\mapsto 0$
for
$[w_1|\cdots |w_k]\mapsto 0$
for
![]() $k>0$
, and the antipode given by
$k>0$
, and the antipode given by
![]() $[w_1|\ldots |w_k]\mapsto (-1)^k [w_k|\ldots |w_1]$
. A linear map
$[w_1|\ldots |w_k]\mapsto (-1)^k [w_k|\ldots |w_1]$
. A linear map
![]() $\phi : W\to W'$
induces a Hopf algebra morphism
$\phi : W\to W'$
induces a Hopf algebra morphism
![]() $\mathrm {Sh}(W)\to \mathrm {Sh}(W')$
, also denoted
$\mathrm {Sh}(W)\to \mathrm {Sh}(W')$
, also denoted
![]() $\phi $
.
$\phi $
.
Let
![]() $z_0\in \tilde C$
. There is a unique linear map
$z_0\in \tilde C$
. There is a unique linear map
satisfying the identities
![]() $I_{z_0}(a)(z_0)=\varepsilon (a)$
and
$I_{z_0}(a)(z_0)=\varepsilon (a)$
and
![]() $d(I_{z_0}([\omega _1|\cdots |\omega _n])= I_{z_0}([\omega _1|\cdots |\omega _{n-1}])\cdot \omega _n$
for any
$d(I_{z_0}([\omega _1|\cdots |\omega _n])= I_{z_0}([\omega _1|\cdots |\omega _{n-1}])\cdot \omega _n$
for any
![]() $n\geq 0$
and
$n\geq 0$
and
![]() $\omega _1,\ldots ,\omega _n\in \Omega (C)$
, so that
$\omega _1,\ldots ,\omega _n\in \Omega (C)$
, so that
![]() $I_{z_0}([\omega _1|\cdots |\omega _n])=\mathrm {int}_{\omega _n}(I_{z_0}([\omega _1|\cdots |\omega _{n-1}]))$
; such a map
$I_{z_0}([\omega _1|\cdots |\omega _n])=\mathrm {int}_{\omega _n}(I_{z_0}([\omega _1|\cdots |\omega _{n-1}]))$
; such a map
![]() $I_{z_0}$
is an algebra morphism, given by iterated integration based at
$I_{z_0}$
is an algebra morphism, given by iterated integration based at
![]() $z_0$
(see [Reference Enriquez and ZerbiniEZ], Lemma 2.2).
$z_0$
(see [Reference Enriquez and ZerbiniEZ], Lemma 2.2).
Set
![]() $\mathrm H_C:=\Omega (C)/d{\mathcal {O}}(C)$
. Let
$\mathrm H_C:=\Omega (C)/d{\mathcal {O}}(C)$
. Let
![]() $\sigma : \mathrm H_C\to \Omega (C)$
be a section of the projection map
$\sigma : \mathrm H_C\to \Omega (C)$
be a section of the projection map
![]() $\Omega (C)\to \mathrm H_C$
.
$\Omega (C)\to \mathrm H_C$
.
Lemma 2.4 ([Reference Enriquez and ZerbiniEZ])
(a) Let
![]() $\sigma _*:\mathrm {Sh}(\mathrm H_C)\to \mathrm {Sh}(\Omega (C))$
be algebra morphism induced by
$\sigma _*:\mathrm {Sh}(\mathrm H_C)\to \mathrm {Sh}(\Omega (C))$
be algebra morphism induced by
![]() $\sigma $
, then
$\sigma $
, then
![]() $\tilde f_{\sigma ,z_0}:=I_{z_0}\circ \sigma : \mathrm {Sh}(\mathrm H_C)\to {\mathcal {O}}_{hol}(\tilde C)$
is an injective algebra morphism.
$\tilde f_{\sigma ,z_0}:=I_{z_0}\circ \sigma : \mathrm {Sh}(\mathrm H_C)\to {\mathcal {O}}_{hol}(\tilde C)$
is an injective algebra morphism.
(b) The image of
![]() $\tilde f_{\sigma ,z_0}$
is independent of
$\tilde f_{\sigma ,z_0}$
is independent of
![]() $z_0$
; it is a subalgebra of
$z_0$
; it is a subalgebra of
![]() ${\mathcal {O}}_{hol}(\tilde C)$
, denoted
${\mathcal {O}}_{hol}(\tilde C)$
, denoted
![]() $\mathcal H_C(\sigma )$
.
$\mathcal H_C(\sigma )$
.
(c) The composition
![]() ${\mathcal {O}}(C) \otimes \mathcal H_C(\sigma )\hookrightarrow {\mathcal {O}}_{hol}(\tilde C)\otimes {\mathcal {O}}_{hol}(\tilde C)\to {\mathcal {O}}_{hol}(\tilde C)$
of the canonical injections with the product map of
${\mathcal {O}}(C) \otimes \mathcal H_C(\sigma )\hookrightarrow {\mathcal {O}}_{hol}(\tilde C)\otimes {\mathcal {O}}_{hol}(\tilde C)\to {\mathcal {O}}_{hol}(\tilde C)$
of the canonical injections with the product map of
![]() ${\mathcal {O}}_{hol}(\tilde C)$
yields an algebra isomorphism
${\mathcal {O}}_{hol}(\tilde C)$
yields an algebra isomorphism
![]() ${\mathcal {O}}(C)\otimes \mathcal H_C(\sigma )\simeq A_C$
.
${\mathcal {O}}(C)\otimes \mathcal H_C(\sigma )\simeq A_C$
.
Proof Statements (a) and (c) are consequences of Theorem A(b) in [Reference Enriquez and ZerbiniEZ] with J equal to the element
![]() $J_\sigma $
defined in Definition 1.2 of [Reference Enriquez and ZerbiniEZ]. Statement (b) follows from [Reference Enriquez and ZerbiniEZ], Theorem A(a).
$J_\sigma $
defined in Definition 1.2 of [Reference Enriquez and ZerbiniEZ]. Statement (b) follows from [Reference Enriquez and ZerbiniEZ], Theorem A(a).
Lemma 2.5 Let
![]() $d:={\mathrm {dim}}({\mathrm {H}}_C)$
and
$d:={\mathrm {dim}}({\mathrm {H}}_C)$
and
![]() $(h_i){}_{i\in [\![1,d]\!]}$
beFootnote
1
a
$(h_i){}_{i\in [\![1,d]\!]}$
beFootnote
1
a
![]() $\mathbb C$
-basis of
$\mathbb C$
-basis of
![]() ${\mathrm {H}}_C$
. Then the family
${\mathrm {H}}_C$
. Then the family
is a
![]() $\mathbb C$
-basis of
$\mathbb C$
-basis of
![]() $\mathcal H_C(\sigma )$
, as well as an
$\mathcal H_C(\sigma )$
, as well as an
![]() ${\mathcal {O}}(C)$
-basis of
${\mathcal {O}}(C)$
-basis of
![]() $A_C$
.
$A_C$
.
Proof The first statement follows from [Reference Enriquez and ZerbiniEZ], Proposition 5.10, and the second statement follows from its combination with Lemma 2.4(c).
Definition 2.6 If
![]() $(\alpha _i)_{i\in [\![1,d]\!]}$
is a family of
$(\alpha _i)_{i\in [\![1,d]\!]}$
is a family of
![]() $\Omega (C)$
whose image in
$\Omega (C)$
whose image in
![]() $\mathrm H_C=\Omega (C)/d({\mathcal {O}}(C))$
is a
$\mathrm H_C=\Omega (C)/d({\mathcal {O}}(C))$
is a
![]() $\mathbb C$
-basis, set
$\mathbb C$
-basis, set
for any
![]() $s\geq 0$
and
$s\geq 0$
and
![]() $i_1,\ldots ,i_s \in [\![1,d]\!]$
.
$i_1,\ldots ,i_s \in [\![1,d]\!]$
.
We call (2.3.2) the hyperlogarithm functions associated with the family
![]() $(\alpha _i)_{i\in [\![1,d]\!]}$
.
$(\alpha _i)_{i\in [\![1,d]\!]}$
.
Lemma 2.7 If
![]() $(\alpha _i)_{i\in [\![1,d]\!]}$
is a family of
$(\alpha _i)_{i\in [\![1,d]\!]}$
is a family of
![]() $\Omega (C)$
as in Definition 2.6, then there exists a unique pair
$\Omega (C)$
as in Definition 2.6, then there exists a unique pair
![]() $(\sigma ,(h_i)_i)$
where
$(\sigma ,(h_i)_i)$
where
![]() $\sigma : \mathrm H_C\to \Omega (C)$
is a section of the projection
$\sigma : \mathrm H_C\to \Omega (C)$
is a section of the projection
![]() $\Omega (C)\to \mathrm H_C$
and
$\Omega (C)\to \mathrm H_C$
and
![]() $(h_i)_{i\in [\![1,d]\!]}$
is a
$(h_i)_{i\in [\![1,d]\!]}$
is a
![]() $\mathbb C$
-basis of
$\mathbb C$
-basis of
![]() $\mathrm H_C$
, such that
$\mathrm H_C$
, such that
![]() $\alpha _i=\sigma (h_i)$
for any i. One then has the identity
$\alpha _i=\sigma (h_i)$
for any i. One then has the identity
Proof This is straightforward.
2.4 Background on elliptic curves
2.4.1 Elliptic curves and coverings
Let us denote by
![]() ${\mathfrak{H}}$
the complex upper half-plane. Until the end of §4, an element
${\mathfrak{H}}$
the complex upper half-plane. Until the end of §4, an element
![]() $\tau $
in
$\tau $
in
![]() ${\mathfrak{H}}$
is fixed. Let
${\mathfrak{H}}$
is fixed. Let
![]() $\Lambda :={\mathbb {Z}}+{\mathbb {Z}}\tau {\subset } {\mathbb {C}}$
.
$\Lambda :={\mathbb {Z}}+{\mathbb {Z}}\tau {\subset } {\mathbb {C}}$
.
Definition 2.8 We set
![]() $\mathcal {E}:=\mathbb {C}/\Lambda $
, and we denote
$\mathcal {E}:=\mathbb {C}/\Lambda $
, and we denote
![]() $pr : \mathbb C\to \mathbb {C}/\Lambda ={\mathcal {E}}$
the canonical projection.
$pr : \mathbb C\to \mathbb {C}/\Lambda ={\mathcal {E}}$
the canonical projection.
![]() ${\mathcal {E}}$
is a compact genus-one Riemann surface, and
${\mathcal {E}}$
is a compact genus-one Riemann surface, and
![]() $pr$
is a universal cover map for
$pr$
is a universal cover map for
![]() ${\mathcal {E}}$
.
${\mathcal {E}}$
.
Definition 2.9 Let S be a finite subset of
![]() ${\mathcal {E}}$
containing
${\mathcal {E}}$
containing
![]() $pr(0)$
. We set
$pr(0)$
. We set
![]() ${\mathcal {E}}_S:=\mathcal {E}\smallsetminus S$
, and we fix a universal cover
${\mathcal {E}}_S:=\mathcal {E}\smallsetminus S$
, and we fix a universal cover
![]() $p:\tilde {{\mathcal {E}}}_S\to {\mathcal {E}}_S$
.
$p:\tilde {{\mathcal {E}}}_S\to {\mathcal {E}}_S$
.
The restriction of
![]() $pr$
is a covering map
$pr$
is a covering map
![]() $\mathbb C\smallsetminus pr^{-1}(S)\to {\mathcal {E}}_S$
. The universal cover map p then admits a factorization
$\mathbb C\smallsetminus pr^{-1}(S)\to {\mathcal {E}}_S$
. The universal cover map p then admits a factorization
![]() $p=\varpi \circ pr$
, where
$p=\varpi \circ pr$
, where
![]() $\varpi :\tilde {{\mathcal {E}}}_S\to \mathbb C\smallsetminus pr^{-1}(S)$
is a universal cover map, so that the following diagram commutes
$\varpi :\tilde {{\mathcal {E}}}_S\to \mathbb C\smallsetminus pr^{-1}(S)$
is a universal cover map, so that the following diagram commutes

Definition 2.10 (a) Let
![]() $s\mapsto \tilde s$
be a section of the map
$s\mapsto \tilde s$
be a section of the map
![]() $pr : pr^{-1}(S)\to S$
such that
$pr : pr^{-1}(S)\to S$
such that
![]() $pr(0)\mapsto 0$
.
$pr(0)\mapsto 0$
.
(b) We denote by
![]() $\tilde S$
the subset of
$\tilde S$
the subset of
![]() $pr^{-1}(S)$
defined as the image of the map
$pr^{-1}(S)$
defined as the image of the map
![]() $s\mapsto \tilde s$
.
$s\mapsto \tilde s$
.
One has
![]() $pr^{-1}(S)=\cup _{s\in S}(\tilde s+\Lambda )$
(equality of subsets of
$pr^{-1}(S)=\cup _{s\in S}(\tilde s+\Lambda )$
(equality of subsets of
![]() $\mathbb C$
).
$\mathbb C$
).
2.4.2 Functions in
 ${\mathcal {O}}_{mer}(\mathbb C,pr^{-1}(S))$
${\mathcal {O}}_{mer}(\mathbb C,pr^{-1}(S))$
For
![]() $r\in \mathbb Z_{\geq 1}$
and
$r\in \mathbb Z_{\geq 1}$
and
![]() $z\in \mathbb C\smallsetminus \Lambda $
, let
$z\in \mathbb C\smallsetminus \Lambda $
, let
where the series is absolutely convergent for
![]() $r>2$
, and is defined by Eisenstein summation for
$r>2$
, and is defined by Eisenstein summation for
![]() $r=1,2$
(see [Reference Broedel, Mafra, Matthes and SchlottererBMMS], footnote 8), and let
$r=1,2$
(see [Reference Broedel, Mafra, Matthes and SchlottererBMMS], footnote 8), and let
![]() $E_r$
be the function
$E_r$
be the function
![]() $z\mapsto E_r(z)$
; then
$z\mapsto E_r(z)$
; then
![]() $E_r$
belongs to
$E_r$
belongs to
![]() ${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
. If
${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
. If
![]() $r\geq 2$
, then the function
$r\geq 2$
, then the function
![]() $E_r$
is elliptic, i.e.,
$E_r$
is elliptic, i.e.,
![]() $\Lambda $
-invariant; on the other hand,
$\Lambda $
-invariant; on the other hand,
![]() $E_1$
satisfies the identitiesFootnote
2
$E_1$
satisfies the identitiesFootnote
2
For every
![]() $r\geq 1$
, the function
$r\geq 1$
, the function
![]() $E_r$
satisfies the identity
$E_r$
satisfies the identity
Moreover, for every
![]() $r\geq 1$
consider also the Eisenstein series
$r\geq 1$
consider also the Eisenstein series
 $$ \begin{align} e_r\,:=\,\sum_{\lambda \in \Lambda\smallsetminus\{0\}}\frac{1}{\lambda^r}\,\in\mathbb C\,, \end{align} $$
$$ \begin{align} e_r\,:=\,\sum_{\lambda \in \Lambda\smallsetminus\{0\}}\frac{1}{\lambda^r}\,\in\mathbb C\,, \end{align} $$
which is again defined via the Eisenstein summation for
![]() $r\leq 2$
, and vanishes when r is odd.
$r\leq 2$
, and vanishes when r is odd.
The Weierstrass
![]() $\wp $
-function attached to
$\wp $
-function attached to
![]() $\Lambda $
is given by
$\Lambda $
is given by
![]() $\wp :=E_2-e_2$
. One then has
$\wp :=E_2-e_2$
. One then has
Definition 2.11 We denote by
![]() $(g_n)_{n\geq 0}$
the family of meromorphic functionsFootnote
3
in
$(g_n)_{n\geq 0}$
the family of meromorphic functionsFootnote
3
in
![]() ${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
defined via the following identity of generating series in the formal variable
${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
defined via the following identity of generating series in the formal variable
![]() $\alpha $
:
$\alpha $
:
 $$ \begin{align} \sum_{n\geq 0}g_n\,\alpha^{n-1}\,:=\,\frac{1}{\alpha}\,\exp\Big(-\sum_{r\geq 1}\frac{(-\alpha)^r}{r}\,(E_r-e_r)\Big)\,. \end{align} $$
$$ \begin{align} \sum_{n\geq 0}g_n\,\alpha^{n-1}\,:=\,\frac{1}{\alpha}\,\exp\Big(-\sum_{r\geq 1}\frac{(-\alpha)^r}{r}\,(E_r-e_r)\Big)\,. \end{align} $$
In particular,
![]() $g_0=1$
and
$g_0=1$
and
![]() $g_1=E_1$
has a simple pole with residue
$g_1=E_1$
has a simple pole with residue
![]() $1$
at all points of
$1$
at all points of
![]() $\Lambda $
. Fourier expansions for the functions
$\Lambda $
. Fourier expansions for the functions
![]() $g_n$
can be found in [Reference Broedel, Mafra, Matthes and SchlottererBMMS], Equations (3.35) and (3.36).
$g_n$
can be found in [Reference Broedel, Mafra, Matthes and SchlottererBMMS], Equations (3.35) and (3.36).
Lemma 2.12 (see [Reference MatthesMa], Prop 2.1.3)
The function
![]() $g_n$
is regular at
$g_n$
is regular at
![]() $0$
for any
$0$
for any
![]() $n\geq 2$
.
$n\geq 2$
.
The left-hand side of (2.4.5) is an element of the ring
![]() ${\mathcal {O}}_{mer}(\mathbb C,\Lambda )((\alpha ))$
of formal Laurent series with coefficients in
${\mathcal {O}}_{mer}(\mathbb C,\Lambda )((\alpha ))$
of formal Laurent series with coefficients in
![]() ${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
, which we denote by F.
${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
, which we denote by F.
Remark 2.13
F is the expansion at
![]() $\alpha =0$
of a meromorphic function of two variables, known as the Kronecker function ([Reference WeilW, Reference ZagierZ2]).
$\alpha =0$
of a meromorphic function of two variables, known as the Kronecker function ([Reference WeilW, Reference ZagierZ2]).
Lemma-Definition 2.14 (a) For every
![]() $a\in pr^{-1}(S)$
and every
$a\in pr^{-1}(S)$
and every
![]() $n\geq 0$
, the function
$n\geq 0$
, the function
![]() $T_ag_n=(z\mapsto g_n(z-a))$
belongs to
$T_ag_n=(z\mapsto g_n(z-a))$
belongs to
![]() ${\mathcal {O}}_{mer}(\mathbb C,pr^{-1}(S))$
.
${\mathcal {O}}_{mer}(\mathbb C,pr^{-1}(S))$
.
(b) Set
![]() $\omega _{n,a}:=T_a(g_n)\cdot dz$
, then
$\omega _{n,a}:=T_a(g_n)\cdot dz$
, then
![]() $\omega _{n,a}$
belongs to
$\omega _{n,a}$
belongs to
![]() $\Omega _{hol}(\mathbb C \smallsetminus pr^{-1}(S))$
.
$\Omega _{hol}(\mathbb C \smallsetminus pr^{-1}(S))$
.
Proof The first statement follows from
![]() $T_a({\mathcal {O}}_{mer}(\mathbb C,\Lambda ))={\mathcal {O}}_{mer}(\mathbb C,a+\Lambda )$
and
$T_a({\mathcal {O}}_{mer}(\mathbb C,\Lambda ))={\mathcal {O}}_{mer}(\mathbb C,a+\Lambda )$
and
![]() $a+\Lambda \subset pr^{-1}(S)$
. The second statement follows from the module structure of
$a+\Lambda \subset pr^{-1}(S)$
. The second statement follows from the module structure of
![]() $\Omega _{hol}(\mathbb C\smallsetminus pr^{-1}(S))$
over
$\Omega _{hol}(\mathbb C\smallsetminus pr^{-1}(S))$
over
![]() ${\mathcal {O}}_{hol}(\mathbb C\smallsetminus pr^{-1}(S))$
, and the inclusion
${\mathcal {O}}_{hol}(\mathbb C\smallsetminus pr^{-1}(S))$
, and the inclusion
![]() ${\mathcal {O}}_{mer}(\mathbb C,\Lambda )\subset \mathcal O_{hol}(\mathbb C\smallsetminus pr^{-1}(S))$
.
${\mathcal {O}}_{mer}(\mathbb C,\Lambda )\subset \mathcal O_{hol}(\mathbb C\smallsetminus pr^{-1}(S))$
.
2.4.3 Functional equations
Lemma 2.15 For every
![]() $n\geq 1$
, one hasFootnote
4
the following equalities in
$n\geq 1$
, one hasFootnote
4
the following equalities in
![]() ${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
:
${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
:
 $$ \begin{align} T_{1}g_{n}\,=\,&g_n\,, \quad\quad \quad (T_{\tau}-id)(g_n)\,=\,\sum_{k=0}^{n-1}\frac{(2\pi \mathrm{i})^{n-k}}{(n-k)!}\, g_k\,, \end{align} $$
$$ \begin{align} T_{1}g_{n}\,=\,&g_n\,, \quad\quad \quad (T_{\tau}-id)(g_n)\,=\,\sum_{k=0}^{n-1}\frac{(2\pi \mathrm{i})^{n-k}}{(n-k)!}\, g_k\,, \end{align} $$
 $$ \begin{align} &g_n'\,=\,\sum_{k=0}^{n-1}(-1)^{n-k}\,E_{n-k+1}\,g_k\,. \end{align} $$
$$ \begin{align} &g_n'\,=\,\sum_{k=0}^{n-1}(-1)^{n-k}\,E_{n-k+1}\,g_k\,. \end{align} $$
Proof Applying (2.4.1) and (2.4.2) to the right-hand side of (2.4.5), we obtain that
 $$ \begin{align*} F(z+1,&\alpha)\,=\,F(z,\alpha)\,, \quad\quad \quad F(z+\tau,\alpha)\,=\,e^{-2\pi i\alpha}\,F(z,\alpha)\,,\\ &\frac{\partial}{\partial z}F(z,\alpha)\,=\,\Big(\sum_{r\geq 1}(-\alpha)^r\,E_{r+1}(z)\Big)\,F(z,\alpha)\,, \end{align*} $$
$$ \begin{align*} F(z+1,&\alpha)\,=\,F(z,\alpha)\,, \quad\quad \quad F(z+\tau,\alpha)\,=\,e^{-2\pi i\alpha}\,F(z,\alpha)\,,\\ &\frac{\partial}{\partial z}F(z,\alpha)\,=\,\Big(\sum_{r\geq 1}(-\alpha)^r\,E_{r+1}(z)\Big)\,F(z,\alpha)\,, \end{align*} $$
(the first line is (3.13) in [Reference Broedel, Mafra, Matthes and SchlottererBMMS]). The statement follows by comparing these identities with the left-hand side of (2.4.5).
Corollary 2.16 For any
![]() $n\geq 0$
and
$n\geq 0$
and
![]() $a\in pr^{-1}(S)$
, one has
$a\in pr^{-1}(S)$
, one has
 $$ \begin{align} \omega_{n,a+1}=\omega_{n,a}, \quad \omega_{n,a+\tau}=\sum_{k=0}^n {(2 \pi \mathrm{i})^{n-k}\over (n-k)!}\omega_{k,a}. \end{align} $$
$$ \begin{align} \omega_{n,a+1}=\omega_{n,a}, \quad \omega_{n,a+\tau}=\sum_{k=0}^n {(2 \pi \mathrm{i})^{n-k}\over (n-k)!}\omega_{k,a}. \end{align} $$
Proof Follows from (2.4.6) and from the invariance of
![]() $dz$
under
$dz$
under
![]() $T_a$
,
$T_a$
,
![]() $a\in pr^{-1}(S)$
.
$a\in pr^{-1}(S)$
.
2.5 An
 ${\mathcal {O}}({\mathcal {E}}_S)$
-basis of
${\mathcal {O}}({\mathcal {E}}_S)$
-basis of
 $A_{{\mathcal {E}}_S}$
arising from elliptic HLs
$A_{{\mathcal {E}}_S}$
arising from elliptic HLs
We introduce the shorthand notation
![]() $O_S:={\mathcal {O}}({\mathcal {E}}_S)$
; then
$O_S:={\mathcal {O}}({\mathcal {E}}_S)$
; then
![]() $O_S$
is a subalgebra of
$O_S$
is a subalgebra of
![]() ${\mathcal {O}}_{mer}(\mathbb C,pr^{-1}(S))$
.
${\mathcal {O}}_{mer}(\mathbb C,pr^{-1}(S))$
.
Definition 2.17
![]() $\partial $
is the derivation of
$\partial $
is the derivation of
![]() $O_S$
arising from the restriction of the action of
$O_S$
arising from the restriction of the action of
![]() $\partial $
on
$\partial $
on
![]() ${\mathcal {O}}_{mer}(\mathbb C,pr^{-1}(S))$
(see Section 1.3.2).
${\mathcal {O}}_{mer}(\mathbb C,pr^{-1}(S))$
(see Section 1.3.2).
Set
![]() $S_\star :=S\sqcup \{\star \}$
. Define a map
$S_\star :=S\sqcup \{\star \}$
. Define a map
![]() $S_\star \to \Omega ({\mathcal {E}}_S)$
,
$S_\star \to \Omega ({\mathcal {E}}_S)$
,
![]() $s\mapsto \alpha _s$
by
$s\mapsto \alpha _s$
by
![]() $\alpha _s:=(T_s-id)(g_1)\cdot dz$
if
$\alpha _s:=(T_s-id)(g_1)\cdot dz$
if
![]() $s\in S\smallsetminus \{0\}$
,
$s\in S\smallsetminus \{0\}$
,
![]() $\alpha _\star :=dz$
,
$\alpha _\star :=dz$
,
![]() $\alpha _0:=E_2\cdot dz$
.
$\alpha _0:=E_2\cdot dz$
.
Lemma 2.18 The family
![]() $(\alpha _s)_{s\in S_\star }$
is a family of
$(\alpha _s)_{s\in S_\star }$
is a family of
![]() $\Omega ({\mathcal {E}}_S)$
whose image in
$\Omega ({\mathcal {E}}_S)$
whose image in
![]() $\mathrm H_{{\mathcal {E}}_S} =\Omega ({\mathcal {E}}_S)/d(O_S)$
is a
$\mathrm H_{{\mathcal {E}}_S} =\Omega ({\mathcal {E}}_S)/d(O_S)$
is a
![]() $\mathbb C$
-basis.
$\mathbb C$
-basis.
Proof The residue map induces a linear map
![]() $O_S/\partial (O_S)\to (\mathbb C^S)_0$
, where
$O_S/\partial (O_S)\to (\mathbb C^S)_0$
, where
![]() $(\mathbb C^S)_0\subset \mathbb C^S$
is the set of tuples whose sum is equal to
$(\mathbb C^S)_0\subset \mathbb C^S$
is the set of tuples whose sum is equal to
![]() $0$
.
$0$
.
If
![]() $f\in O_S$
is a representative of an element of the kernel of
$f\in O_S$
is a representative of an element of the kernel of
![]() $O_S/\partial (O_S)\to (\mathbb C^S)_0$
, then the residue of
$O_S/\partial (O_S)\to (\mathbb C^S)_0$
, then the residue of
![]() $fdz$
at any
$fdz$
at any
![]() $s\in S$
is zero, so that the function
$s\in S$
is zero, so that the function
![]() $z\mapsto \int _{z_0}^z f(u)du$
is single-valued around each
$z\mapsto \int _{z_0}^z f(u)du$
is single-valued around each
![]() $s\in S$
. It follows that there exist
$s\in S$
. It follows that there exist
![]() $a,b\in \mathbb C$
such that
$a,b\in \mathbb C$
such that
![]() $z\mapsto \int _{z_0}^z f(u)du-az-bg_1(z)$
belongs to
$z\mapsto \int _{z_0}^z f(u)du-az-bg_1(z)$
belongs to
![]() $O_S$
, and therefore
$O_S$
, and therefore
![]() $f\equiv a+bg^{\prime }_1=a-bE_2$
mod
$f\equiv a+bg^{\prime }_1=a-bE_2$
mod
![]() $\partial (O_S)$
. This implies that the kernel of
$\partial (O_S)$
. This implies that the kernel of
![]() $O_S/\partial (O_S)\to (\mathbb C^S)_0$
is spanned by
$O_S/\partial (O_S)\to (\mathbb C^S)_0$
is spanned by
![]() $1$
and
$1$
and
![]() $E_2$
.
$E_2$
.
The map
![]() $O_S/\partial (O_S)\to (\mathbb C^S)_0$
is surjective, because a preimage of
$O_S/\partial (O_S)\to (\mathbb C^S)_0$
is surjective, because a preimage of
![]() $(a_s)_s\in (\mathbb C^S)_0$
is
$(a_s)_s\in (\mathbb C^S)_0$
is
![]() $\sum _{s\in S}a_sT_{\tilde s}(g_1)$
. Therefore
$\sum _{s\in S}a_sT_{\tilde s}(g_1)$
. Therefore
![]() $O_S/\partial (O_S)$
fits in an exact sequence
$O_S/\partial (O_S)$
fits in an exact sequence
A basis of
![]() $O_S/\partial (O_S)$
is therefore the union of a basis of
$O_S/\partial (O_S)$
is therefore the union of a basis of
![]() $\mathrm {Span}_{\mathbb C}(1,E_2)$
and of the preimage of a basis of
$\mathrm {Span}_{\mathbb C}(1,E_2)$
and of the preimage of a basis of
![]() $(\mathbb C^S)_0$
. Since
$(\mathbb C^S)_0$
. Since
![]() $(1,E_2)$
is linearly independent and since
$(1,E_2)$
is linearly independent and since
![]() ${((T_{\tilde s}-id)(g_1))_{s\in S\smallsetminus \{0\}}}$
is such a preimage, the image of
${((T_{\tilde s}-id)(g_1))_{s\in S\smallsetminus \{0\}}}$
is such a preimage, the image of
in
![]() $O_S/\partial (O_S)$
forms a
$O_S/\partial (O_S)$
forms a
![]() $\mathbb C$
-basis of
$\mathbb C$
-basis of
![]() $O_S/\partial (O_S)$
.
$O_S/\partial (O_S)$
.
The linear isomorphism
![]() $-\cdot dz : O_S\to \Omega ({\mathcal {E}}_S)$
,
$-\cdot dz : O_S\to \Omega ({\mathcal {E}}_S)$
,
![]() $f\mapsto f\cdot dz$
is such that
$f\mapsto f\cdot dz$
is such that
![]() $(-\cdot dz) \circ \partial =d$
(equality of linear maps
$(-\cdot dz) \circ \partial =d$
(equality of linear maps
![]() $O_S\to \Omega ({\mathcal {E}}_S)$
). This linear isomorphism therefore induces a linear isomorphism
$O_S\to \Omega ({\mathcal {E}}_S)$
). This linear isomorphism therefore induces a linear isomorphism
![]() $-\cdot dz : O_S/\partial (O_S)\to \Omega ({\mathcal {E}}_S)/d(O_S)$
. The statement follows from this and from the fact that the claimed family is the image of (2.5.1) by
$-\cdot dz : O_S/\partial (O_S)\to \Omega ({\mathcal {E}}_S)/d(O_S)$
. The statement follows from this and from the fact that the claimed family is the image of (2.5.1) by
![]() $-\cdot dz$
.
$-\cdot dz$
.
Corollary 2.19 The family
is an
![]() $O_S$
-basis of the
$O_S$
-basis of the
![]() $O_S$
-module
$O_S$
-module
![]() $A_{{\mathcal {E}}_S}$
.
$A_{{\mathcal {E}}_S}$
.
3 The multivalued functions
 $\tilde \Gamma $
from [Reference Broedel, Duhr, Dulat and TancrediBDDT]
$\tilde \Gamma $
from [Reference Broedel, Duhr, Dulat and TancrediBDDT]
The article [Reference Broedel, Duhr, Dulat and TancrediBDDT] introduces a family of functions
![]() $\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
, with
$\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
, with
![]() $r\geq 0$
,
$r\geq 0$
,
![]() $n_i\geq 0$
and
$n_i\geq 0$
and
![]() $a_i\in pr^{-1}(S)$
forFootnote
5
$a_i\in pr^{-1}(S)$
forFootnote
5
![]() $i\in [\![1,r]\!]$
, which are multivalued functions on
$i\in [\![1,r]\!]$
, which are multivalued functions on
![]() $\mathbb C\smallsetminus pr^{-1}(S)$
defined as regularized iterated integrals of the forms
$\mathbb C\smallsetminus pr^{-1}(S)$
defined as regularized iterated integrals of the forms
![]() $(\omega _{n,a})_{n\geq 0,a\in pr^{-1}(S)}$
from Section 2.4, where the integration path starts at 0. It follows from the functional equation (2.4.8) that this vector space is spanned by the collection of the same functions, where the parameters satisfy the restricted condition
$(\omega _{n,a})_{n\geq 0,a\in pr^{-1}(S)}$
from Section 2.4, where the integration path starts at 0. It follows from the functional equation (2.4.8) that this vector space is spanned by the collection of the same functions, where the parameters satisfy the restricted condition
![]() $a_i\in \tilde S$
for any
$a_i\in \tilde S$
for any
![]() $i\in [\![1,r]\!]$
. Since one of the possible forms, namely
$i\in [\![1,r]\!]$
. Since one of the possible forms, namely
![]() $\omega _{1,0}$
, has a pole at this point, regularisation is needed for the definition of the functions
$\omega _{1,0}$
, has a pole at this point, regularisation is needed for the definition of the functions
![]() $\tilde \Gamma $
even in the restricted case.
$\tilde \Gamma $
even in the restricted case.
The regularization procedure indicated in [Reference Broedel, Duhr, Dulat and TancrediBDDT] relies on replacing the endpoint 0 by a small
![]() $\epsilon $
and extracting a value from the asymptotic expansion in
$\epsilon $
and extracting a value from the asymptotic expansion in
![]() $\epsilon $
; this procedure was rigourously carried out in a similar situation in [Reference Burgos Gil and FresanBGF], Section 3.8, which is based on the “tangential base points” ideas of [Reference DeligneDe], Section 15. On the other hand, the regularization procedure indicated in [Reference Broedel and KaderliBK] for the definition of the functions
$\epsilon $
; this procedure was rigourously carried out in a similar situation in [Reference Burgos Gil and FresanBGF], Section 3.8, which is based on the “tangential base points” ideas of [Reference DeligneDe], Section 15. On the other hand, the regularization procedure indicated in [Reference Broedel and KaderliBK] for the definition of the functions
![]() $\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
is an analog of the procedure from [Reference BrownBr], §5.1 (see also [Reference PanzerPa], Section 3.3), for the definition of hyperlogarithm functions in genus zero, which relies on a decomposition result for the shuffle algebra of a vector space (see Lem 3.13).
$\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
is an analog of the procedure from [Reference BrownBr], §5.1 (see also [Reference PanzerPa], Section 3.3), for the definition of hyperlogarithm functions in genus zero, which relies on a decomposition result for the shuffle algebra of a vector space (see Lem 3.13).
We show that both the “tangential base point” and the “shuffle” regularization procedures amount to the construction of algebra morphisms ![]() (Section 3.1, Lemma 3.10 and Section 3.2, Lemma 3.14) where V is a suitable vector space, which we show to coincide (Section 3.2, Lem 3.15). In Section 3.3, we then apply the construction of these two equal morphisms to the definition of the functions
(Section 3.1, Lemma 3.10 and Section 3.2, Lemma 3.14) where V is a suitable vector space, which we show to coincide (Section 3.2, Lem 3.15). In Section 3.3, we then apply the construction of these two equal morphisms to the definition of the functions
![]() $\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
and to the proof of their properties.
$\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
and to the proof of their properties.
3.1 Tangential base point regularisation
For each
![]() $z_0\in \tilde {{\mathcal {E}}}_S$
, the linear map
$z_0\in \tilde {{\mathcal {E}}}_S$
, the linear map
![]() $I_{z_0}$
defined in (2.3.1) extends to a unique linear map
$I_{z_0}$
defined in (2.3.1) extends to a unique linear map
satisfying the identities
![]() $I_{z_0}(a)(z_0)=\varepsilon (a)$
and
$I_{z_0}(a)(z_0)=\varepsilon (a)$
and
![]() $d(I_{z_0}([\omega _1|\cdots |\omega _n])= I_{z_0}([\omega _1|\cdots |\omega _{n-1}])\cdot \omega _n$
for any
$d(I_{z_0}([\omega _1|\cdots |\omega _n])= I_{z_0}([\omega _1|\cdots |\omega _{n-1}])\cdot \omega _n$
for any
![]() $n\geq 0$
and
$n\geq 0$
and
![]() $\omega _1,\ldots ,\omega _n\in \Omega _{hol}(\tilde {{\mathcal {E}}}_S)$
; then
$\omega _1,\ldots ,\omega _n\in \Omega _{hol}(\tilde {{\mathcal {E}}}_S)$
; then
![]() $I_{z_0}$
is an algebra morphism, given by iterated integration based at
$I_{z_0}$
is an algebra morphism, given by iterated integration based at
![]() $z_0$
.
$z_0$
.
Definition 3.1 (a) V is the complex vector space freely generated by the symbols
![]() $\left (\begin {smallmatrix}n\\a\end {smallmatrix}\right )$
, where
$\left (\begin {smallmatrix}n\\a\end {smallmatrix}\right )$
, where
![]() $(n,a)\in \mathbb Z_{\geq 0}\times \tilde S$
, where
$(n,a)\in \mathbb Z_{\geq 0}\times \tilde S$
, where
![]() $\tilde S$
is as in Definition 2.10(b).
$\tilde S$
is as in Definition 2.10(b).
(b)
![]() $V_+\subset V$
is the vector subspace generated by
$V_+\subset V$
is the vector subspace generated by
![]() $\left (\begin {smallmatrix}n\\a\end {smallmatrix}\right )$
, where
$\left (\begin {smallmatrix}n\\a\end {smallmatrix}\right )$
, where
![]() $(n,a)\neq (1,0)$
.
$(n,a)\neq (1,0)$
.
(c)
![]() $\mathrm {Sh}^*(V)$
is the subspace
$\mathrm {Sh}^*(V)$
is the subspace
![]() $\mathbb C1\oplus [V_+|\mathrm {Sh}(V)]$
of
$\mathbb C1\oplus [V_+|\mathrm {Sh}(V)]$
of
![]() $\mathrm {Sh}(V)$
.
$\mathrm {Sh}(V)$
.
One checks that
![]() $\mathrm {Sh}^*(V)$
is a subalgebra of
$\mathrm {Sh}^*(V)$
is a subalgebra of
![]() $\mathrm {Sh}(V)$
.
$\mathrm {Sh}(V)$
.
Definition 3.2 (a)
![]() $\kappa : V\to \Omega _{hol}(\tilde {{\mathcal {E}}}_S)$
is the linear map induced by
$\kappa : V\to \Omega _{hol}(\tilde {{\mathcal {E}}}_S)$
is the linear map induced by
![]() $\left (\begin {smallmatrix}n\\a\end {smallmatrix}\right ) \mapsto \omega _{n,a}$
for any
$\left (\begin {smallmatrix}n\\a\end {smallmatrix}\right ) \mapsto \omega _{n,a}$
for any
![]() $(n,a)\in \mathbb Z_{\geq 0}\times \tilde S$
.
$(n,a)\in \mathbb Z_{\geq 0}\times \tilde S$
.
(b) We denote by
![]() $\kappa _* : \mathrm {Sh}(V)\to \mathrm {Sh}(\Omega _{hol}(\tilde {{\mathcal {E}}}_S))$
the induced Hopf algebra morphism.
$\kappa _* : \mathrm {Sh}(V)\to \mathrm {Sh}(\Omega _{hol}(\tilde {{\mathcal {E}}}_S))$
the induced Hopf algebra morphism.
(c) For
![]() $z_0\in \tilde {{\mathcal {E}}}_S$
,
$z_0\in \tilde {{\mathcal {E}}}_S$
,
![]() $k_{z_0} : \mathrm {Sh}(V)\to {\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
is the composed algebra morphism
$k_{z_0} : \mathrm {Sh}(V)\to {\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
is the composed algebra morphism
![]() $I_{z_0}\circ \kappa _*$
.
$I_{z_0}\circ \kappa _*$
.
We fix
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $]0,\delta [\subset \mathbb {C}\smallsetminus pr^{-1}(S)$
; we fix a continuous map
$]0,\delta [\subset \mathbb {C}\smallsetminus pr^{-1}(S)$
; we fix a continuous map
![]() $\mathrm {sect} : \,]0,\delta [\to \tilde {{\mathcal {E}}}_S$
such that
$\mathrm {sect} : \,]0,\delta [\to \tilde {{\mathcal {E}}}_S$
such that
![]() $\varpi \circ \mathrm {sect}$
is the canonical inclusion.
$\varpi \circ \mathrm {sect}$
is the canonical inclusion.
Definition 3.3
![]() $\mathcal F\subset \mathbb C^{]0,\delta [}$
is the set of functions
$\mathcal F\subset \mathbb C^{]0,\delta [}$
is the set of functions
![]() $\phi : \,]0,\delta [\to \mathbb C$
, such that for some
$\phi : \,]0,\delta [\to \mathbb C$
, such that for some
![]() $\alpha>0$
one has
$\alpha>0$
one has
![]() $\phi (t)=O(t^{1-\alpha })$
when
$\phi (t)=O(t^{1-\alpha })$
when
![]() $t\to 0$
.
$t\to 0$
.
Lemma 3.4 (a) The map
![]() $\mathbb C[X]\otimes \mathcal F\to \mathcal F$
given by
$\mathbb C[X]\otimes \mathcal F\to \mathcal F$
given by
![]() $P\otimes \phi \mapsto P\bullet \phi :=(t\mapsto P(\log (t))\phi (t))$
is well-defined and makes
$P\otimes \phi \mapsto P\bullet \phi :=(t\mapsto P(\log (t))\phi (t))$
is well-defined and makes
![]() $\mathcal F$
into a
$\mathcal F$
into a
![]() $\mathbb C[X]$
-module.
$\mathbb C[X]$
-module.
(b) The direct sum
![]() $\mathbb C[X]\oplus \mathcal F$
, equipped with the product given by
$\mathbb C[X]\oplus \mathcal F$
, equipped with the product given by
![]() $(P,\phi )\cdot (Q,\psi )=(PQ,P\bullet \psi +Q\bullet \phi +\phi \psi )$
, is a commutative and associative algebra.
$(P,\phi )\cdot (Q,\psi )=(PQ,P\bullet \psi +Q\bullet \phi +\phi \psi )$
, is a commutative and associative algebra.
(c) The algebra from (b) is equipped with a pair of algebra morphisms
where
![]() $\mathrm {ev}(P,\phi ):=\phi (0)$
and
$\mathrm {ev}(P,\phi ):=\phi (0)$
and
![]() $\mathrm {can}(P,\phi ):=(t\mapsto P(\log (t))+\phi (t))$
, and the algebra morphism
$\mathrm {can}(P,\phi ):=(t\mapsto P(\log (t))+\phi (t))$
, and the algebra morphism
![]() $\mathrm {can}$
is injective.
$\mathrm {can}$
is injective.
Proof (a) follows from the fact that for any
![]() $r\geq 0$
, one has
$r\geq 0$
, one has
![]() $(\log (t))^r=O(t^{-\alpha })$
at the neighborhood of
$(\log (t))^r=O(t^{-\alpha })$
at the neighborhood of
![]() $0$
for any
$0$
for any
![]() $\alpha>0$
. (b) is an immediate direct check. Let us prove (c). The fact that
$\alpha>0$
. (b) is an immediate direct check. Let us prove (c). The fact that
![]() $\mathrm {ev}$
and
$\mathrm {ev}$
and
![]() $\mathrm {can}$
are algebra morphisms can be verified directly. Let us prove the injectivity of
$\mathrm {can}$
are algebra morphisms can be verified directly. Let us prove the injectivity of
![]() $\mathrm {can}$
(see also [BGF], Lemma 3.350). Assume that
$\mathrm {can}$
(see also [BGF], Lemma 3.350). Assume that
![]() $(P,\phi )\in \mathbb C[X]\oplus \mathcal F$
and
$(P,\phi )\in \mathbb C[X]\oplus \mathcal F$
and
![]() $\mathrm {can}(P,\phi )=0$
. If P is nonzero, let
$\mathrm {can}(P,\phi )=0$
. If P is nonzero, let
![]() $d\geq 0$
be its degree and
$d\geq 0$
be its degree and
![]() $a_dX^d$
be its dominant term. Then
$a_dX^d$
be its dominant term. Then
![]() $\mathrm {can}(P,\phi )(t)\sim a_d(\log (t))^d$
at the neighborhood of
$\mathrm {can}(P,\phi )(t)\sim a_d(\log (t))^d$
at the neighborhood of
![]() $0$
, which contradicts
$0$
, which contradicts
![]() $\mathrm {can}(P,\phi )=0$
, therefore
$\mathrm {can}(P,\phi )=0$
, therefore
![]() $P=0$
. Then
$P=0$
. Then
![]() $\mathrm {can}(0,\phi )=\phi $
, which implies
$\mathrm {can}(0,\phi )=\phi $
, which implies
![]() $\phi =0$
.
$\phi =0$
.
In what follows, we will view
![]() $\mathbb C[X]\oplus \mathcal F$
as a subalgebra of
$\mathbb C[X]\oplus \mathcal F$
as a subalgebra of
![]() $\mathbb C^{]0,\delta [}$
, making use of the injectivity of the morphism
$\mathbb C^{]0,\delta [}$
, making use of the injectivity of the morphism
![]() $\mathrm {can}$
.
$\mathrm {can}$
.
Lemma 3.5 For
![]() $a\in \mathrm {Sh}(V)$
and
$a\in \mathrm {Sh}(V)$
and
![]() $z\in \tilde {{\mathcal {E}}}_S$
, denote by
$z\in \tilde {{\mathcal {E}}}_S$
, denote by
![]() $k(a,z)$
the assignment
$k(a,z)$
the assignment
![]() $]0,\delta [\,\ni t\mapsto k_{\mathrm {sect}(t)}(a)(z)\in \mathbb C$
; then
$]0,\delta [\,\ni t\mapsto k_{\mathrm {sect}(t)}(a)(z)\in \mathbb C$
; then
![]() $k(a,z)\in \mathbb C^{]0,\delta [}$
. For any
$k(a,z)\in \mathbb C^{]0,\delta [}$
. For any
![]() $z\in \tilde {{\mathcal {E}}}_S$
, the map
$z\in \tilde {{\mathcal {E}}}_S$
, the map
![]() $a\mapsto k(a,z)$
is an algebra morphism
$a\mapsto k(a,z)$
is an algebra morphism
![]() $\mathrm {Sh}(V)\to \mathbb C^{]0,\delta [}$
.
$\mathrm {Sh}(V)\to \mathbb C^{]0,\delta [}$
.
Proof This follows from the fact that for any
![]() $z\in \tilde {{\mathcal {E}}}_S$
and
$z\in \tilde {{\mathcal {E}}}_S$
and
![]() $t\in ]0,\delta [$
, the map
$t\in ]0,\delta [$
, the map
![]() $a\mapsto k_{\mathrm {sect}(t)}(a)(z)$
is an algebra morphism
$a\mapsto k_{\mathrm {sect}(t)}(a)(z)$
is an algebra morphism
![]() $\mathrm {Sh}(V)\to \mathbb C$
(see Definition 4.2(c)).
$\mathrm {Sh}(V)\to \mathbb C$
(see Definition 4.2(c)).
Lemma 3.6 For each
![]() $z\in \tilde {{\mathcal {E}}}_S$
, there exists a complex number
$z\in \tilde {{\mathcal {E}}}_S$
, there exists a complex number
![]() $G(z)$
such that the function
$G(z)$
such that the function
![]() $]0,\delta [\,\ni t\mapsto \int _{\mathrm {sect}(t)}^z\omega _{1,0}+\mathrm {log}(t)$
belongs to
$]0,\delta [\,\ni t\mapsto \int _{\mathrm {sect}(t)}^z\omega _{1,0}+\mathrm {log}(t)$
belongs to
![]() $G(z)+\mathcal F$
. Then
$G(z)+\mathcal F$
. Then
![]() $G\in {\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
and
$G\in {\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
and
![]() $(t\mapsto G(\mathrm {sect}(t)))\in (t\mapsto \mathrm {log}(t)) +\mathcal F$
.
$(t\mapsto G(\mathrm {sect}(t)))\in (t\mapsto \mathrm {log}(t)) +\mathcal F$
.
Proof Since
![]() $\omega _{1,0}$
has a pole of order
$\omega _{1,0}$
has a pole of order
![]() $1$
at
$1$
at
![]() $0$
, for any
$0$
, for any
![]() $z\in \tilde {{\mathcal {E}}}_S$
, the map
$z\in \tilde {{\mathcal {E}}}_S$
, the map
![]() $t\mapsto \int _{\mathrm {sect}(t)}^z \omega _{1,0}+\mathrm {log}(t)$
is an analytic function; denoting by
$t\mapsto \int _{\mathrm {sect}(t)}^z \omega _{1,0}+\mathrm {log}(t)$
is an analytic function; denoting by
![]() $G(z)$
its value at 0, it therefore belongs to
$G(z)$
its value at 0, it therefore belongs to
![]() $G(z)+\mathcal F$
. One then has
$G(z)+\mathcal F$
. One then has
![]() $G(z) =G(\mathrm {sect}(\delta /2))+\int _{\mathrm {sect}(\delta /2)}^z \omega _{1,0}$
for any
$G(z) =G(\mathrm {sect}(\delta /2))+\int _{\mathrm {sect}(\delta /2)}^z \omega _{1,0}$
for any
![]() $z\in \tilde {{\mathcal {E}}}_S$
, which implies the holomorphicity statement.
$z\in \tilde {{\mathcal {E}}}_S$
, which implies the holomorphicity statement.
Notice that one has
 $$ \begin{align} \mathrm{Sh}(V)=\oplus_{r\geq 0}[\underbrace{\left(\begin{smallmatrix}1\\0\end{smallmatrix}\right)|\ldots| \left(\begin{smallmatrix}1\\0\end{smallmatrix}\right)}_{r\text{ factors}}|\mathrm{Sh}^*(V)]. \end{align} $$
$$ \begin{align} \mathrm{Sh}(V)=\oplus_{r\geq 0}[\underbrace{\left(\begin{smallmatrix}1\\0\end{smallmatrix}\right)|\ldots| \left(\begin{smallmatrix}1\\0\end{smallmatrix}\right)}_{r\text{ factors}}|\mathrm{Sh}^*(V)]. \end{align} $$
Definition 3.7 (a) The degree of an element
![]() $a\in \mathrm {Sh}(V)$
is
$a\in \mathrm {Sh}(V)$
is
![]() $-\infty $
if
$-\infty $
if
![]() $a=0$
, and is the maximum of the set of integers
$a=0$
, and is the maximum of the set of integers
![]() $r\geq 0$
such that the projection of a in the r-th component of the decomposition (3.1.1) is nonzero if
$r\geq 0$
such that the projection of a in the r-th component of the decomposition (3.1.1) is nonzero if
![]() $a\neq 0$
.
$a\neq 0$
.
(b) The degree of an element of
![]() $\mathbb C[X]\oplus \mathcal F$
is the polynomial degree of the first component.
$\mathbb C[X]\oplus \mathcal F$
is the polynomial degree of the first component.
Lemma 3.8 (a) For
![]() $a\in \mathrm {Sh}(V)$
and
$a\in \mathrm {Sh}(V)$
and
![]() $z\in \tilde {{\mathcal {E}}}_S$
, one has
$z\in \tilde {{\mathcal {E}}}_S$
, one has
![]() $k(a,z)\in \mathbb C[X]\oplus \mathcal F$
, and
$k(a,z)\in \mathbb C[X]\oplus \mathcal F$
, and
![]() $\mathrm {deg}(k(a,z))\leq \mathrm {deg}(a)$
.
$\mathrm {deg}(k(a,z))\leq \mathrm {deg}(a)$
.
(b) For any
![]() $z\in \tilde {{\mathcal {E}}}_S$
, the map
$z\in \tilde {{\mathcal {E}}}_S$
, the map
![]() $\mathrm {Sh(V)}\ni a\mapsto k(a,z)\in \mathbb C[X]\oplus \mathcal F$
is an algebra morphism.
$\mathrm {Sh(V)}\ni a\mapsto k(a,z)\in \mathbb C[X]\oplus \mathcal F$
is an algebra morphism.
Proof (a) By (3.1.1), it suffices to prove that for any
![]() $r\geq 0$
and
$r\geq 0$
and
 $a\in [\underbrace {\left (\begin {smallmatrix}1\\0\end {smallmatrix}\right )|\ldots | \left (\begin {smallmatrix}1\\0\end {smallmatrix}\right )}_{r\text { factors}}|a^*]$
, with
$a\in [\underbrace {\left (\begin {smallmatrix}1\\0\end {smallmatrix}\right )|\ldots | \left (\begin {smallmatrix}1\\0\end {smallmatrix}\right )}_{r\text { factors}}|a^*]$
, with
![]() $a^*\in \mathrm {Sh}^*(V)$
, one has
$a^*\in \mathrm {Sh}^*(V)$
, one has
![]() $k(a,z)\in \mathbb C[X]_{\leq r}\oplus \mathcal F$
. The element
$k(a,z)\in \mathbb C[X]_{\leq r}\oplus \mathcal F$
. The element
![]() $k(a,z)\in \mathbb C^{]0,\delta [}$
is the map taking
$k(a,z)\in \mathbb C^{]0,\delta [}$
is the map taking
![]() $t\in \,]0,\delta [$
to the first term of the sequence of equalities
$t\in \,]0,\delta [$
to the first term of the sequence of equalities
 $$ \begin{align*} &I_{\mathrm{sect}(t)}([\underbrace{\omega_{1,0}|\ldots|\omega_{1,0}}_{r\text{ factors}}|\kappa(a^*)])(z) =I_{\mathrm{sect}(t)}([\underbrace{dG|\ldots|dG}_{r\text{ factors}}|\kappa_*(a^*)])(z) \\ &=\frac{1}{r!}\,I_{\mathrm{sect}(t)}\big([(G-G(\mathrm{sect}(t)))^r \odot \kappa_*(a^*)]\big)(z) \\ & =\sum_{l=0}^r \frac{1}{l!(r-l)!}\,(-G(\mathrm{sect}(t))^l I_{\mathrm{sect}(t)}\big([G^{r-l}\odot \kappa_*(a^*)]\big)(z) \end{align*} $$
$$ \begin{align*} &I_{\mathrm{sect}(t)}([\underbrace{\omega_{1,0}|\ldots|\omega_{1,0}}_{r\text{ factors}}|\kappa(a^*)])(z) =I_{\mathrm{sect}(t)}([\underbrace{dG|\ldots|dG}_{r\text{ factors}}|\kappa_*(a^*)])(z) \\ &=\frac{1}{r!}\,I_{\mathrm{sect}(t)}\big([(G-G(\mathrm{sect}(t)))^r \odot \kappa_*(a^*)]\big)(z) \\ & =\sum_{l=0}^r \frac{1}{l!(r-l)!}\,(-G(\mathrm{sect}(t))^l I_{\mathrm{sect}(t)}\big([G^{r-l}\odot \kappa_*(a^*)]\big)(z) \end{align*} $$
where
![]() $\odot $
is the linear map
$\odot $
is the linear map
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)\otimes \mathrm {Sh}({\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)) \to \mathrm {Sh}({\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S))$
given by
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)\otimes \mathrm {Sh}({\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)) \to \mathrm {Sh}({\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S))$
given by
![]() $f\odot (a_1\otimes \cdots \otimes a_n):=(fa_1)\otimes \cdots \otimes a_n$
. One shows that for any
$f\odot (a_1\otimes \cdots \otimes a_n):=(fa_1)\otimes \cdots \otimes a_n$
. One shows that for any
![]() $l\in [\![0,r]\!]$
, the map
$l\in [\![0,r]\!]$
, the map
![]() ${t\mapsto I_{\mathrm {sect}(t)}[G^{r-l}\odot \kappa _*(a^*)]}$
belongs to
${t\mapsto I_{\mathrm {sect}(t)}[G^{r-l}\odot \kappa _*(a^*)]}$
belongs to
![]() $\mathbb C+\mathcal F$
. It follows from Lemma 3.6 that for any
$\mathbb C+\mathcal F$
. It follows from Lemma 3.6 that for any
![]() $l\in [\![0,r]\!]$
, the function
$l\in [\![0,r]\!]$
, the function
![]() $t\mapsto (-G(\mathrm {sect}(t))^l$
belongs to
$t\mapsto (-G(\mathrm {sect}(t))^l$
belongs to
![]() $(t\mapsto (\mathrm {log}(t))^l)+\mathcal F$
. Since
$(t\mapsto (\mathrm {log}(t))^l)+\mathcal F$
. Since
![]() $((t\mapsto (\mathrm {log}(t))^l)+\mathcal F)\cdot (\mathbb C+\mathcal F)\subset \mathbb C(t\mapsto (\mathrm {log}(t))^l)+\mathcal F$
,
$((t\mapsto (\mathrm {log}(t))^l)+\mathcal F)\cdot (\mathbb C+\mathcal F)\subset \mathbb C(t\mapsto (\mathrm {log}(t))^l)+\mathcal F$
,
![]() $k(a,z)$
belongs to
$k(a,z)$
belongs to
![]() $\sum _{l=0}^r \mathbb C(t\mapsto (\mathrm {log}(t))^l)+\mathcal F$
, which is
$\sum _{l=0}^r \mathbb C(t\mapsto (\mathrm {log}(t))^l)+\mathcal F$
, which is
![]() $\mathbb C[X]_{\leq r}+\mathcal F$
.
$\mathbb C[X]_{\leq r}+\mathcal F$
.
Statement (b) follows from (a), Lemma 3.5 and the injectivity of
![]() $\mathrm {can}$
(see Lemma 3.4(c)).
$\mathrm {can}$
(see Lemma 3.4(c)).
Definition 3.9 For
![]() $a\in \mathrm {Sh}(V)$
,
$a\in \mathrm {Sh}(V)$
,
![]() $k_{\overrightarrow 0}(a)\in \mathbb C^{\tilde {{\mathcal {E}}}_S}$
is the function
$k_{\overrightarrow 0}(a)\in \mathbb C^{\tilde {{\mathcal {E}}}_S}$
is the function
![]() $\tilde {{\mathcal {E}}}_S\to \mathbb C$
given by
$\tilde {{\mathcal {E}}}_S\to \mathbb C$
given by
![]() $z\mapsto k_{\overrightarrow 0}(a)(z):=\mathrm {ev}(k(a,z))$
.
$z\mapsto k_{\overrightarrow 0}(a)(z):=\mathrm {ev}(k(a,z))$
.
Lemma 3.10 (a) The map
![]() $\mathrm {Sh}(V)\to \mathbb C^{\tilde {{\mathcal {E}}}_S}$
given by
$\mathrm {Sh}(V)\to \mathbb C^{\tilde {{\mathcal {E}}}_S}$
given by
![]() $a\mapsto k_{\overrightarrow 0}(a)$
is an algebra morphism.
$a\mapsto k_{\overrightarrow 0}(a)$
is an algebra morphism.
(b) For
![]() $z\in \tilde {{\mathcal {E}}}_S$
,
$z\in \tilde {{\mathcal {E}}}_S$
,
![]() $a\in \mathrm {Sh}(V)$
, one has
$a\in \mathrm {Sh}(V)$
, one has
where we denote
![]() $\Delta (a)$
as
$\Delta (a)$
as
![]() $a^{(1)}\otimes a^{(2)}$
(equality in
$a^{(1)}\otimes a^{(2)}$
(equality in
![]() $\mathbb C[X]\oplus \mathcal F$
).
$\mathbb C[X]\oplus \mathcal F$
).
(c) For any
![]() $a\in \mathrm {Sh}(V)$
,
$a\in \mathrm {Sh}(V)$
,
![]() $k_{\overrightarrow 0}(a)$
belongs to the subalgebra
$k_{\overrightarrow 0}(a)$
belongs to the subalgebra
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)\subset \mathbb C^{\tilde {{\mathcal {E}}}_S}$
.
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)\subset \mathbb C^{\tilde {{\mathcal {E}}}_S}$
.
(d) The map
![]() $k_{\overrightarrow 0} : \mathrm {Sh}(V)\to {\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
is an algebra morphism.
$k_{\overrightarrow 0} : \mathrm {Sh}(V)\to {\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
is an algebra morphism.
Proof (a) For each
![]() $z\in \tilde {{\mathcal {E}}}_S$
, the composition
$z\in \tilde {{\mathcal {E}}}_S$
, the composition
![]() $\mathrm {Sh}(V)\stackrel {k(-,z)}{\to } \mathbb C[X]\oplus \mathcal F\stackrel {\mathrm {ev}}{\to }\mathbb C$
is an algebra morphism as it is a composition of such morphisms (see Lemma 3.8(b) and Lemma 3.4(c)). The map
$\mathrm {Sh}(V)\stackrel {k(-,z)}{\to } \mathbb C[X]\oplus \mathcal F\stackrel {\mathrm {ev}}{\to }\mathbb C$
is an algebra morphism as it is a composition of such morphisms (see Lemma 3.8(b) and Lemma 3.4(c)). The map
![]() $k_{\overrightarrow 0} : \mathrm {Sh}(V)\to \mathbb C^{\tilde {{\mathcal {E}}}_S}$
is the composition
$k_{\overrightarrow 0} : \mathrm {Sh}(V)\to \mathbb C^{\tilde {{\mathcal {E}}}_S}$
is the composition
![]() $\mathrm {Sh}(V)\to \mathrm {Sh}(V)^{\tilde {{\mathcal {E}}}_S}\to \mathbb C^{\tilde {{\mathcal {E}}}_S}$
, where the first map is the diagonal morphism and the second map is the product
$\mathrm {Sh}(V)\to \mathrm {Sh}(V)^{\tilde {{\mathcal {E}}}_S}\to \mathbb C^{\tilde {{\mathcal {E}}}_S}$
, where the first map is the diagonal morphism and the second map is the product
![]() $\prod _{z\in \tilde {{\mathcal {E}}}_S}(\mathrm {ev}\circ k(-,z))$
. Since both the diagonal morphism and
$\prod _{z\in \tilde {{\mathcal {E}}}_S}(\mathrm {ev}\circ k(-,z))$
. Since both the diagonal morphism and
![]() $\mathrm {ev}\circ k(-,z)$
are algebra morphisms for each
$\mathrm {ev}\circ k(-,z)$
are algebra morphisms for each
![]() $z\in \tilde {{\mathcal {E}}}_S$
,
$z\in \tilde {{\mathcal {E}}}_S$
,
![]() $k_{\overrightarrow 0}$
is an algebra morphism, which proves (a).
$k_{\overrightarrow 0}$
is an algebra morphism, which proves (a).
(b) Both sides belong to
![]() $\mathbb C[X]\oplus \mathcal F$
, which is contained in
$\mathbb C[X]\oplus \mathcal F$
, which is contained in
![]() $\mathbb C^{]0,\delta [}$
, so it suffices the prove that they coincide as functions on
$\mathbb C^{]0,\delta [}$
, so it suffices the prove that they coincide as functions on
![]() $]0,\delta [$
. For
$]0,\delta [$
. For
![]() $t\in \,]0,\delta [$
, one has
$t\in \,]0,\delta [$
, one has
 $$ \begin{align*} k(a,z)(t) &=k_{\mathrm{sect}(t)}(a)(z)=k_{\mathrm{sect}(t)}(a^{(1)})(\mathrm{sect}(\delta/2)) k_{\mathrm{sect}(\delta/2)}(a^{(2)})(z) \\ & =k(a^{(1)},\mathrm{sect}(\delta/2))(t)\cdot k_{\mathrm{sect}(\delta/2)}(a^{(2)})(z) \end{align*} $$
$$ \begin{align*} k(a,z)(t) &=k_{\mathrm{sect}(t)}(a)(z)=k_{\mathrm{sect}(t)}(a^{(1)})(\mathrm{sect}(\delta/2)) k_{\mathrm{sect}(\delta/2)}(a^{(2)})(z) \\ & =k(a^{(1)},\mathrm{sect}(\delta/2))(t)\cdot k_{\mathrm{sect}(\delta/2)}(a^{(2)})(z) \end{align*} $$
where the first and last equalities follow from definitions, and the middle equality follows from [Reference Enriquez and ZerbiniEZ], Lemma 2.5.
(c) Applying
![]() $\mathrm {ev}$
to the identity of (b), for any
$\mathrm {ev}$
to the identity of (b), for any
![]() $a\in \mathrm {Sh}(V)$
and any
$a\in \mathrm {Sh}(V)$
and any
![]() $z\in \tilde {{\mathcal {E}}}_S$
one finds
$z\in \tilde {{\mathcal {E}}}_S$
one finds
(equality in
![]() $\mathbb C$
). Since, for any
$\mathbb C$
). Since, for any
![]() $b\in \mathrm {Sh}(V)$
, the map
$b\in \mathrm {Sh}(V)$
, the map
![]() $z\mapsto k_{\mathrm {sect}(\delta /2)}(a^{(2)})(z)$
belongs to
$z\mapsto k_{\mathrm {sect}(\delta /2)}(a^{(2)})(z)$
belongs to
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)\subset \mathbb C^{\tilde {{\mathcal {E}}}_S}$
, it follows that the map
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)\subset \mathbb C^{\tilde {{\mathcal {E}}}_S}$
, it follows that the map
![]() $z\mapsto k_{\overrightarrow 0}(a)(z)$
also belongs to
$z\mapsto k_{\overrightarrow 0}(a)(z)$
also belongs to
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
.
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
.
(d) This statement follows from (a) and (c).
3.2 Shuffle regularization
We now present the construction of the algebra morphism ![]() . In this approach, Lemma 3.4 is replaced by:
. In this approach, Lemma 3.4 is replaced by:
Lemma 3.11 Let us equip
![]() $\mathbb C\oplus \mathcal F$
with the algebra structure such that
$\mathbb C\oplus \mathcal F$
with the algebra structure such that
![]() $1\in \mathbb C$
is the unity and
$1\in \mathbb C$
is the unity and
![]() $\mathcal F$
is a nonunital subalgebra. There is a diagram of algebra morphisms
$\mathcal F$
is a nonunital subalgebra. There is a diagram of algebra morphisms
where
![]() $\mathrm {ev}_0$
is the projection
$\mathrm {ev}_0$
is the projection
![]() $\mathbb C\oplus \mathcal F\to \mathbb C$
and
$\mathbb C\oplus \mathcal F\to \mathbb C$
and
![]() $\mathrm {can}_0(\lambda ,\phi )=\lambda +\phi $
.
$\mathrm {can}_0(\lambda ,\phi )=\lambda +\phi $
.
Proof Obvious.
Remark 3.12 The diagram from Lemma 3.11 is the pull-back of the diagram
![]() $\mathbb C\leftarrow C([0,\delta [) \hookrightarrow \mathbb C^{]0,\delta [}$
by the corestriction
$\mathbb C\leftarrow C([0,\delta [) \hookrightarrow \mathbb C^{]0,\delta [}$
by the corestriction
![]() $\mathbb C\oplus \mathcal F\to C([0,\delta [)$
of
$\mathbb C\oplus \mathcal F\to C([0,\delta [)$
of
![]() $\mathrm {can}_0$
, where
$\mathrm {can}_0$
, where
![]() $C([0,\delta [)$
is the space of continuous complex functions on
$C([0,\delta [)$
is the space of continuous complex functions on
![]() $[0,\delta [$
, where
$[0,\delta [$
, where
![]() $C([0,\delta [)\to \mathbb C$
is the evaluation at
$C([0,\delta [)\to \mathbb C$
is the evaluation at
![]() $0$
and where
$0$
and where
![]() $C([0,\delta [)\hookrightarrow \mathbb C^{]0,\delta [}$
is the natural inclusion.
$C([0,\delta [)\hookrightarrow \mathbb C^{]0,\delta [}$
is the natural inclusion.
One also uses the following.
Lemma 3.13 (see [Reference PanzerPa], Lemma 3.2.4)
There exists a unique algebra isomorphism
![]() $\mathrm {Sh}^*(V)[X]\to \mathrm {Sh}(V)$
given by
$\mathrm {Sh}^*(V)[X]\to \mathrm {Sh}(V)$
given by
![]() $a\mapsto a$
for
$a\mapsto a$
for
![]() $a\in \mathrm {Sh}^*(V)$
and
$a\in \mathrm {Sh}^*(V)$
and
![]() $X\mapsto \left (\begin {smallmatrix}1\\0\end {smallmatrix}\right )$
.
$X\mapsto \left (\begin {smallmatrix}1\\0\end {smallmatrix}\right )$
.
Lemma-Definition 3.14 (a) For
![]() $a\in \mathrm {Sh}^*(V)$
and
$a\in \mathrm {Sh}^*(V)$
and
![]() $z\in \tilde {{\mathcal {E}}}_S$
, the function
$z\in \tilde {{\mathcal {E}}}_S$
, the function
![]() $]0,\delta [\ni t\mapsto k_{\mathrm {sect}(t)}(a)(z)$
belongs to
$]0,\delta [\ni t\mapsto k_{\mathrm {sect}(t)}(a)(z)$
belongs to
![]() $\mathbb C\oplus \mathcal F$
; denote by
$\mathbb C\oplus \mathcal F$
; denote by ![]() its image by
its image by
![]() $\mathrm {ev}_0$
. Then, for any
$\mathrm {ev}_0$
. Then, for any
![]() $z\in \tilde {{\mathcal {E}}}_S$
,
$z\in \tilde {{\mathcal {E}}}_S$
,
![]() $a\mapsto (t\mapsto k_{\mathrm {sect}(t)}(a)(z))$
is an algebra morphism
$a\mapsto (t\mapsto k_{\mathrm {sect}(t)}(a)(z))$
is an algebra morphism
![]() $\mathrm {Sh}^*(V)\to \mathbb C\oplus \mathcal F$
, and
$\mathrm {Sh}^*(V)\to \mathbb C\oplus \mathcal F$
, and ![]() is an algebra morphism
is an algebra morphism
![]() $\mathrm {Sh}^*(V)\to \mathbb C$
.
$\mathrm {Sh}^*(V)\to \mathbb C$
.
(b) For
![]() $a\in \mathrm {Sh}^*(V)$
, the function
$a\in \mathrm {Sh}^*(V)$
, the function ![]() belongs to
belongs to
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
; we denote by
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
; we denote by ![]() the map taking a to this function. Then
the map taking a to this function. Then ![]() is an algebra morphism.
is an algebra morphism.
(c) There is a unique algebra morphism ![]() that extends
that extends ![]() and such that
and such that
![]() $\left (\begin {smallmatrix}1\\0\end {smallmatrix}\right )\mapsto G$
.
$\left (\begin {smallmatrix}1\\0\end {smallmatrix}\right )\mapsto G$
.
Proof (a) The first statement follows from the specialization of Lemma 3.8(a) for
![]() $\mathrm {deg}(a)\leq 0$
. The second statement follows from the fact that for any pair
$\mathrm {deg}(a)\leq 0$
. The second statement follows from the fact that for any pair
![]() $(z,t)$
, the map
$(z,t)$
, the map
![]() $a\mapsto k_{\mathrm {sect}(t)}(a)(z)$
is an algebra morphism
$a\mapsto k_{\mathrm {sect}(t)}(a)(z)$
is an algebra morphism
![]() $\mathrm {Sh}^*(V)\to \mathbb C$
, and from the first statement; the last statement follows from the second statement by composing with
$\mathrm {Sh}^*(V)\to \mathbb C$
, and from the first statement; the last statement follows from the second statement by composing with
![]() $\mathrm {ev}_0$
.
$\mathrm {ev}_0$
.
(b) Let
![]() $a\in \mathrm {Sh}^*(V)$
. Since
$a\in \mathrm {Sh}^*(V)$
. Since
![]() $\Delta (\mathrm {Sh}^*(V))\subset \mathrm {Sh}^*(V)\otimes \mathrm {Sh}(V)$
, the equality from Lemma 3.10(b) takes place in
$\Delta (\mathrm {Sh}^*(V))\subset \mathrm {Sh}^*(V)\otimes \mathrm {Sh}(V)$
, the equality from Lemma 3.10(b) takes place in
![]() $\mathbb C\oplus \mathcal F$
. Applying
$\mathbb C\oplus \mathcal F$
. Applying
![]() $\mathrm {ev}_0$
to it, one obtains that for every
$\mathrm {ev}_0$
to it, one obtains that for every
![]() $z\in \tilde {{\mathcal {E}}}_S$
$z\in \tilde {{\mathcal {E}}}_S$
(equality in
![]() $\mathbb C$
). The first part of (b) then follows from the fact that for any
$\mathbb C$
). The first part of (b) then follows from the fact that for any
![]() $a\in \mathrm {Sh}(V)$
, the map
$a\in \mathrm {Sh}(V)$
, the map
![]() $z\mapsto k_{\mathrm {sect}(\delta /2)}(a^{(2)})(z)$
belongs to
$z\mapsto k_{\mathrm {sect}(\delta /2)}(a^{(2)})(z)$
belongs to
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)\subset \mathbb C^{\tilde {{\mathcal {E}}}_S}$
. The second part of (b) follows from its first part, combined with statement that the maps
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)\subset \mathbb C^{\tilde {{\mathcal {E}}}_S}$
. The second part of (b) follows from its first part, combined with statement that the maps ![]() is an algebra morphism
is an algebra morphism
![]() $\mathrm {Sh}^*(V)\to \mathbb C^{\tilde {{\mathcal {E}}}_S}$
, which follows from (a).
$\mathrm {Sh}^*(V)\to \mathbb C^{\tilde {{\mathcal {E}}}_S}$
, which follows from (a).
(c) This follows from (b) and from Lemma 3.13.
Proposition 3.15 One has ![]() .
.
Proof One checks that the restrictions of
![]() $k_{\overrightarrow 0}$
and
$k_{\overrightarrow 0}$
and ![]() to
to
![]() $\mathrm {Sh}^*(V)$
coincide. Let us compute
$\mathrm {Sh}^*(V)$
coincide. Let us compute
![]() $k_{\overrightarrow 0}(\left (\begin {smallmatrix}1\\0\end {smallmatrix}\right ))$
. For
$k_{\overrightarrow 0}(\left (\begin {smallmatrix}1\\0\end {smallmatrix}\right ))$
. For
![]() $z\in \tilde {{\mathcal {E}}}_S$
,
$z\in \tilde {{\mathcal {E}}}_S$
,
![]() $k(\left (\begin {smallmatrix}1\\0\end {smallmatrix}\right ),z)$
is the function
$k(\left (\begin {smallmatrix}1\\0\end {smallmatrix}\right ),z)$
is the function
![]() $]0,\delta [\, \ni t\mapsto k_{\mathrm {sect}(t)}(\left (\begin {smallmatrix}1\\0\end {smallmatrix}\right )) (z)=\int _{\mathrm {sect}(t)}^z \omega _{1,0}$
. By Lemma 3.6, this function belongs to
$]0,\delta [\, \ni t\mapsto k_{\mathrm {sect}(t)}(\left (\begin {smallmatrix}1\\0\end {smallmatrix}\right )) (z)=\int _{\mathrm {sect}(t)}^z \omega _{1,0}$
. By Lemma 3.6, this function belongs to
![]() $(t\mapsto -\mathrm {log}(t)+G(z))+\mathcal F=P(\mathrm {log}(t))+\mathcal F$
, where
$(t\mapsto -\mathrm {log}(t)+G(z))+\mathcal F=P(\mathrm {log}(t))+\mathcal F$
, where
![]() $P(X)=G(z)-X\in \mathbb C[X]$
. It follows that
$P(X)=G(z)-X\in \mathbb C[X]$
. It follows that ![]() , hence that
, hence that ![]() . By Lemma 3.13, this implies the statement.
. By Lemma 3.13, this implies the statement.
Lemma 3.16 (a) For any
![]() $z_0\in \tilde {{\mathcal {E}}}_S$
and any
$z_0\in \tilde {{\mathcal {E}}}_S$
and any
![]() $a\in \mathrm {Sh}(V)$
one has the equality (in
$a\in \mathrm {Sh}(V)$
one has the equality (in
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
)
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
)
(b) For any
![]() $z_0\in \tilde {{\mathcal {E}}}_S$
, the images of the morphisms
$z_0\in \tilde {{\mathcal {E}}}_S$
, the images of the morphisms
![]() $k_{z_0}$
and
$k_{z_0}$
and
![]() $k_{\overrightarrow 0} : \mathrm {Sh}(V)\to {\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
coincide.
$k_{\overrightarrow 0} : \mathrm {Sh}(V)\to {\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
coincide.
Proof (a) Fix
![]() $a\in \mathrm {Sh}(V)$
and
$a\in \mathrm {Sh}(V)$
and
![]() $z\in \tilde {{\mathcal {E}}}_S$
. By [Reference Enriquez and ZerbiniEZ], Lemma 2.5, one has the identity
$z\in \tilde {{\mathcal {E}}}_S$
. By [Reference Enriquez and ZerbiniEZ], Lemma 2.5, one has the identity
![]() $k_{\mathrm {sect}(t)}(a)(z)=k_{\mathrm {sect}(t)}(a^{(1)})(z_0)\cdot k_{z_0}(a^{(2)})(z)$
for any
$k_{\mathrm {sect}(t)}(a)(z)=k_{\mathrm {sect}(t)}(a^{(1)})(z_0)\cdot k_{z_0}(a^{(2)})(z)$
for any
![]() $t\in \,]0,\delta [$
. One derives from this the equality (in
$t\in \,]0,\delta [$
. One derives from this the equality (in
![]() $\mathbb C^{]0,\delta [}$
)
$\mathbb C^{]0,\delta [}$
)
![]() $(t\mapsto k_{\mathrm {sect}(t)}(a)(z))=(t\mapsto k_{\mathrm {sect}(t)}(a^{(1)})(z_0)) \cdot k_{z_0}(a^{(2)})(z)$
. Since both sides actually belong to the subalgebra
$(t\mapsto k_{\mathrm {sect}(t)}(a)(z))=(t\mapsto k_{\mathrm {sect}(t)}(a^{(1)})(z_0)) \cdot k_{z_0}(a^{(2)})(z)$
. Since both sides actually belong to the subalgebra
![]() $\mathbb C[X]\oplus \mathcal F\subset \mathbb C^{]0,\delta [}$
, then this may be viewed as an equality in
$\mathbb C[X]\oplus \mathcal F\subset \mathbb C^{]0,\delta [}$
, then this may be viewed as an equality in
![]() $\mathbb C[X]\oplus \mathcal F$
. Applying to both sides the morphism
$\mathbb C[X]\oplus \mathcal F$
. Applying to both sides the morphism
![]() $\mathrm {ev} : \mathbb C[X]\oplus \mathcal F\to \mathbb C$
, one derives the equality (in
$\mathrm {ev} : \mathbb C[X]\oplus \mathcal F\to \mathbb C$
, one derives the equality (in
![]() $\mathbb C$
)
$\mathbb C$
)
![]() $k_{\overrightarrow 0}(a)(z)=k_{\overrightarrow 0}(a^{(1)})(z_0)\cdot k_{z_0}(a^{(2)})(z)$
.
$k_{\overrightarrow 0}(a)(z)=k_{\overrightarrow 0}(a^{(1)})(z_0)\cdot k_{z_0}(a^{(2)})(z)$
.
It follows that, for any
![]() $a\in \mathrm {Sh}(V)$
, one has
$a\in \mathrm {Sh}(V)$
, one has
![]() $(z\mapsto k_{\overrightarrow 0}(a)(z))=(z\mapsto k_{\overrightarrow 0}(a^{(1)})(z_0)) \cdot k_{z_0}(a^{(2)})(z)$
(equality in
$(z\mapsto k_{\overrightarrow 0}(a)(z))=(z\mapsto k_{\overrightarrow 0}(a^{(1)})(z_0)) \cdot k_{z_0}(a^{(2)})(z)$
(equality in
![]() $\mathbb C^{\tilde {{\mathcal {E}}}_S}$
). Both sides actually belong to
$\mathbb C^{\tilde {{\mathcal {E}}}_S}$
). Both sides actually belong to
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
, and are respectively equal to the two sides of (3.2.1), which proves (a).
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
, and are respectively equal to the two sides of (3.2.1), which proves (a).
(b) Equation (3.2.1) implies the inclusion
![]() $k_{\overrightarrow 0}(\mathrm {Sh}(V)) \subset k_{z_0}(\mathrm {Sh}(V))$
, and also implies the relation
$k_{\overrightarrow 0}(\mathrm {Sh}(V)) \subset k_{z_0}(\mathrm {Sh}(V))$
, and also implies the relation
![]() $k_{z_0}(a)=k_{\overrightarrow 0}(S(a^{(1)}))(z_0) \cdot k_{\overrightarrow 0}(a^{(2)})$
for any
$k_{z_0}(a)=k_{\overrightarrow 0}(S(a^{(1)}))(z_0) \cdot k_{\overrightarrow 0}(a^{(2)})$
for any
![]() $a \in \mathrm {Sh}(V)$
, where S is the antipode of
$a \in \mathrm {Sh}(V)$
, where S is the antipode of
![]() $\mathrm {Sh}(V)$
, which implies the opposite inclusion
$\mathrm {Sh}(V)$
, which implies the opposite inclusion
![]() $k_{z_0}(\mathrm {Sh}(V)) \subset k_{\overrightarrow 0}(\mathrm {Sh}(V))$
.
$k_{z_0}(\mathrm {Sh}(V)) \subset k_{\overrightarrow 0}(\mathrm {Sh}(V))$
.
3.3 The functions
 $\tilde \Gamma $
$\tilde \Gamma $
Definition 3.17 (see [Reference Broedel, Duhr, Dulat and TancrediBDDT], Equation (4.13))
For any
![]() $r\geq 1$
, any
$r\geq 1$
, any
![]() $n_1,\ldots ,n_r\geq 0$
and any
$n_1,\ldots ,n_r\geq 0$
and any
![]() $a_1,\ldots ,a_r\in \tilde S$
, one defines the function
$a_1,\ldots ,a_r\in \tilde S$
, one defines the function
![]() $\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )\in \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
by
$\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )\in \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
by
One also sets
![]() $\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}\\\end {smallmatrix};-\right ):=1$
for
$\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}\\\end {smallmatrix};-\right ):=1$
for
![]() $r=0$
.
$r=0$
.
It follows from Proposition 3.15 that
![]() $\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}1\\0\end {smallmatrix};-\right )=G$
.
$\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}1\\0\end {smallmatrix};-\right )=G$
.
Lemma 3.18 (see also [Reference PanzerPa], Lemma 3.3.4)
For any
![]() $t\in \mathrm {Sh}(V$
) and
$t\in \mathrm {Sh}(V$
) and
![]() $(n,a) \in \mathbb Z_{\geq 0}\times \tilde S$
, one has
$(n,a) \in \mathbb Z_{\geq 0}\times \tilde S$
, one has
(equality in
![]() $\Omega _{hol}(\tilde {{\mathcal {E}}}_S)$
). Equivalent formulation: for any
$\Omega _{hol}(\tilde {{\mathcal {E}}}_S)$
). Equivalent formulation: for any
![]() $n_1,\ldots ,n_r\geq 0$
and
$n_1,\ldots ,n_r\geq 0$
and
![]() $a_1,\ldots ,a_r\in \tilde S$
, one has
$a_1,\ldots ,a_r\in \tilde S$
, one has
Proof The identity
for any t and
![]() $(n,a)$
as above follows from [Reference Enriquez and ZerbiniEZ], Equation (2.1.1). Let us define the map
$(n,a)$
as above follows from [Reference Enriquez and ZerbiniEZ], Equation (2.1.1). Let us define the map
![]() $\partial ^V : \mathrm {Sh}(V)\to \mathrm {Sh}(V)\otimes V$
by setting
$\partial ^V : \mathrm {Sh}(V)\to \mathrm {Sh}(V)\otimes V$
by setting
![]() $\partial ^V(1)=0$
and
$\partial ^V(1)=0$
and
![]() $\partial ^V([t|v]):=t\,\otimes \,v$
for any
$\partial ^V([t|v]):=t\,\otimes \,v$
for any
![]() $t\in \mathrm {Sh}(V)$
and
$t\in \mathrm {Sh}(V)$
and
![]() $v\in V$
. For
$v\in V$
. For
![]() $t\in \mathrm {Sh}(V)$
, denote
$t\in \mathrm {Sh}(V)$
, denote
![]() $\partial ^V(t)$
by
$\partial ^V(t)$
by
![]() $t^{[1]} \otimes t^{[2]}$
. Then (3.3.2) implies the identity
$t^{[1]} \otimes t^{[2]}$
. Then (3.3.2) implies the identity
where
![]() $\omega : V\to \Omega _{hol}(\tilde {{\mathcal {E}}}_S)$
is the map given by
$\omega : V\to \Omega _{hol}(\tilde {{\mathcal {E}}}_S)$
is the map given by
![]() $\left (\begin {smallmatrix}n\\a\end {smallmatrix}\right )\mapsto \omega _{n,a}$
.
$\left (\begin {smallmatrix}n\\a\end {smallmatrix}\right )\mapsto \omega _{n,a}$
.
Applying Lemma 3.16 with
![]() $z_0:=\mathrm {sect}(\delta /2)$
, one finds that, for any
$z_0:=\mathrm {sect}(\delta /2)$
, one finds that, for any
![]() $t\in \mathrm {Sh}(V)$
,
$t\in \mathrm {Sh}(V)$
,
(equality in
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
), which gives rise to the first equality in
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
), which gives rise to the first equality in
 $$ \begin{align*} d(k_{\overrightarrow 0}(t)) &=k_{\overrightarrow 0}(t^{(1)})(\mathrm{sect}(\delta/2))\cdot d(k_{\mathrm{sect}(\delta/2)}(t^{(2)})) \\ &=k_{\overrightarrow 0}(t^{(1)})(\mathrm{sect}(\delta/2))\cdot k_{\mathrm{sect}(\delta/2)}((t^{(2)})^{[1]}) \cdot\omega((t^{(2)})^{[2]}) \\ & =k_{\overrightarrow 0}((t^{[1]})^{(1)})(\mathrm{sect}(\delta/2))\cdot k_{\mathrm{sect}(\delta/2)}((t^{[1]})^{(2)}) \cdot\omega(t^{[2]})\\& =k_{\overrightarrow 0}(t^{[1]}) \cdot \omega(t^{[2]}), \end{align*} $$
$$ \begin{align*} d(k_{\overrightarrow 0}(t)) &=k_{\overrightarrow 0}(t^{(1)})(\mathrm{sect}(\delta/2))\cdot d(k_{\mathrm{sect}(\delta/2)}(t^{(2)})) \\ &=k_{\overrightarrow 0}(t^{(1)})(\mathrm{sect}(\delta/2))\cdot k_{\mathrm{sect}(\delta/2)}((t^{(2)})^{[1]}) \cdot\omega((t^{(2)})^{[2]}) \\ & =k_{\overrightarrow 0}((t^{[1]})^{(1)})(\mathrm{sect}(\delta/2))\cdot k_{\mathrm{sect}(\delta/2)}((t^{[1]})^{(2)}) \cdot\omega(t^{[2]})\\& =k_{\overrightarrow 0}(t^{[1]}) \cdot \omega(t^{[2]}), \end{align*} $$
where the second equality follows from (3.3.3), the third equality follows from
![]() $(id\otimes \partial ^V)\circ \Delta =(\Delta \otimes id) \circ \partial ^V$
, and the fourth equality follows from (3.3.4). One derives
$(id\otimes \partial ^V)\circ \Delta =(\Delta \otimes id) \circ \partial ^V$
, and the fourth equality follows from (3.3.4). One derives
![]() $d(k_{\overrightarrow 0}(t))=k_{\overrightarrow 0}(t^{[1]}) \cdot \omega (t^{[2]})$
, from which the claimed identity follows.
$d(k_{\overrightarrow 0}(t))=k_{\overrightarrow 0}(t^{[1]}) \cdot \omega (t^{[2]})$
, from which the claimed identity follows.
4 Expression of a basis of the algebra
 $A_{{\mathcal {E}}_S}$
in terms of the functions
$A_{{\mathcal {E}}_S}$
in terms of the functions
 $\tilde \Gamma $
$\tilde \Gamma $
Recall the notation
![]() $O_S:=\mathcal {O}(\mathcal {E}_S)$
from Section 2.5. The purpose of this section is to show that the collection of functions
$O_S:=\mathcal {O}(\mathcal {E}_S)$
from Section 2.5. The purpose of this section is to show that the collection of functions
![]() $\tilde \Gamma $
gives rise to a basis of
$\tilde \Gamma $
gives rise to a basis of
![]() $A_{{\mathcal {E}}_S}$
over
$A_{{\mathcal {E}}_S}$
over
![]() $O_S$
(Theorem 4.27), alternative to the family of elliptic HLs (see §2.5). For this, we introduce an algebra
$O_S$
(Theorem 4.27), alternative to the family of elliptic HLs (see §2.5). For this, we introduce an algebra
![]() $\mathcal G$
generated by the functions
$\mathcal G$
generated by the functions
![]() $\tilde \Gamma $
and show its inclusion in
$\tilde \Gamma $
and show its inclusion in
![]() $A_{{\mathcal {E}}_S}$
(§4.1). In §§4.2 and 4.3, we carry out a precise analysis of differential algebras related to
$A_{{\mathcal {E}}_S}$
(§4.1). In §§4.2 and 4.3, we carry out a precise analysis of differential algebras related to
![]() ${\mathcal {E}}_S$
, which enables us in §4.4 to prove the equality
${\mathcal {E}}_S$
, which enables us in §4.4 to prove the equality
![]() $\mathcal G=A_{{\mathcal {E}}_S}$
(see Theorem 4.20). In §4.5, we prove a linear independence result for the functions
$\mathcal G=A_{{\mathcal {E}}_S}$
(see Theorem 4.20). In §4.5, we prove a linear independence result for the functions
![]() $\tilde \Gamma $
(see Proposition 4.26), based on the criterion of [Reference Deneufchâtel, Duchamp, Minh, Solomon and WinklerDDMS], thereby proving Theorem 4.27. In §4.6, we give examples of the relations implied by Theorem 4.27 between the functions
$\tilde \Gamma $
(see Proposition 4.26), based on the criterion of [Reference Deneufchâtel, Duchamp, Minh, Solomon and WinklerDDMS], thereby proving Theorem 4.27. In §4.6, we give examples of the relations implied by Theorem 4.27 between the functions
![]() $\tilde \Gamma $
and the elliptic HLs from Section 2.5.
$\tilde \Gamma $
and the elliptic HLs from Section 2.5.
4.1 The algebra
 $\mathcal G$
and its inclusion in
$\mathcal G$
and its inclusion in
 $A_{{\mathcal {E}}_S}$
$A_{{\mathcal {E}}_S}$
Definition 4.1
![]() $\mathcal {G}$
is the subalgebra of
$\mathcal {G}$
is the subalgebra of
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
generated by
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
generated by
![]() $O_S[g_1]$
and by the functions
$O_S[g_1]$
and by the functions
![]() $\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
, where
$\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
, where
![]() $r\geq 0$
,
$r\geq 0$
,
![]() $n_1,\ldots ,n_r\geq 0$
and
$n_1,\ldots ,n_r\geq 0$
and
![]() $a_1,\ldots ,a_r\in \tilde S$
(see Definition 3.17), namely
$a_1,\ldots ,a_r\in \tilde S$
(see Definition 3.17), namely
In this definition, the subalgebra
![]() $O_S[g_1]$
of
$O_S[g_1]$
of
![]() ${\mathcal {O}}_{hol}(\mathbb C\smallsetminus pr^{-1}(S))$
is viewed as a subalgebra of
${\mathcal {O}}_{hol}(\mathbb C\smallsetminus pr^{-1}(S))$
is viewed as a subalgebra of
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
via the morphism
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
via the morphism
![]() $\varpi ^* : {\mathcal {O}}_{hol}(\mathbb C\smallsetminus pr^{-1}(S))\to {\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
.
$\varpi ^* : {\mathcal {O}}_{hol}(\mathbb C\smallsetminus pr^{-1}(S))\to {\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
.
Recall now the filtration
![]() $F_\bullet ^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
of the algebra
$F_\bullet ^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
of the algebra
![]() $\mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
defined in Section 2.2.
$\mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
defined in Section 2.2.
Lemma 4.2 For any
![]() $n\geq 0$
and
$n\geq 0$
and
![]() $\tilde s\in \tilde S$
, one has
$\tilde s\in \tilde S$
, one has
![]() $T_{\tilde s}g_n\in F_n^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
.
$T_{\tilde s}g_n\in F_n^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
.
Proof Let
![]() $\tilde s\in \tilde S$
. It follows from (2.4.7) that the collection of functions
$\tilde s\in \tilde S$
. It follows from (2.4.7) that the collection of functions
![]() $(T_{\tilde s}g_n)_{n\geq 0}$
satisfies the relation
$(T_{\tilde s}g_n)_{n\geq 0}$
satisfies the relation
![]() $d(T_{\tilde s}g_n)=\sum _{k=0}^{n-1}(-1)^{n-k}\,T_{\tilde s}g_k\cdot T_{\tilde s}(E_{n-k+1})\cdot dz$
for any
$d(T_{\tilde s}g_n)=\sum _{k=0}^{n-1}(-1)^{n-k}\,T_{\tilde s}g_k\cdot T_{\tilde s}(E_{n-k+1})\cdot dz$
for any
![]() $n\geq 1$
. Let us prove the statement by induction on
$n\geq 1$
. Let us prove the statement by induction on
![]() $n\geq 0$
. For
$n\geq 0$
. For
![]() $n=0$
, one has
$n=0$
, one has
![]() $T_{\tilde s}g_0=1\in F_0^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
. Assume that
$T_{\tilde s}g_0=1\in F_0^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
. Assume that
![]() $T_{\tilde s}g_k\in F_k^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
for
$T_{\tilde s}g_k\in F_k^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
for
![]() $k<n$
. Since
$k<n$
. Since
![]() $T_{\tilde s}E_{l}\in {\mathcal {O}}({\mathcal {E}}_S)$
for
$T_{\tilde s}E_{l}\in {\mathcal {O}}({\mathcal {E}}_S)$
for
![]() $l\geq 2$
, one has
$l\geq 2$
, one has
![]() $T_{\tilde s}(E_l)\cdot dz \in \Omega ({\mathcal {E}}_S)$
for these values of l, hence
$T_{\tilde s}(E_l)\cdot dz \in \Omega ({\mathcal {E}}_S)$
for these values of l, hence
![]() $d(T_{\tilde s}g_n)=\sum _{k=0}^{n-1}(-1)^{n-k}T_{\tilde s}g_k \cdot T_{\tilde s}(E_{n-k+1})\cdot dz\in F_{n-1}^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)\cdot p^*\Omega ({\mathcal {E}}_S)$
, and therefore
$d(T_{\tilde s}g_n)=\sum _{k=0}^{n-1}(-1)^{n-k}T_{\tilde s}g_k \cdot T_{\tilde s}(E_{n-k+1})\cdot dz\in F_{n-1}^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)\cdot p^*\Omega ({\mathcal {E}}_S)$
, and therefore
![]() $T_{\tilde s}g_n\in F_n^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
.
$T_{\tilde s}g_n\in F_n^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
.
Proposition 4.3 For any
![]() $r\geq 0$
, any
$r\geq 0$
, any
![]() $n_1,\ldots ,n_r\geq 0$
and any
$n_1,\ldots ,n_r\geq 0$
and any
![]() $a_1,\ldots ,a_r\in \tilde S$
, the function
$a_1,\ldots ,a_r\in \tilde S$
, the function
![]() $\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
belongs to
$\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
belongs to
![]() $F^\delta _{r+n_1+\cdots +n_r}\mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
.
$F^\delta _{r+n_1+\cdots +n_r}\mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
.
Proof Let us prove the statement by induction on r. If
![]() $r=0$
, the statement is clear. If
$r=0$
, the statement is clear. If
![]() $r>0$
, assume the statement to be true until
$r>0$
, assume the statement to be true until
![]() $r-1$
, so that
$r-1$
, so that
![]() $\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r-1}\\a_1 &a_2 &\ldots &a_{r-1}\end {smallmatrix};-\right )$
belongs to
$\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r-1}\\a_1 &a_2 &\ldots &a_{r-1}\end {smallmatrix};-\right )$
belongs to
![]() $F^\delta _{r-1+n_1+\cdots +n_{r-1}}\mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
. By Lemma 4.2(b), one has
$F^\delta _{r-1+n_1+\cdots +n_{r-1}}\mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
. By Lemma 4.2(b), one has
![]() $T_{a_r}g_{n_r}\in F_{n_r}^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
. The facts that
$T_{a_r}g_{n_r}\in F_{n_r}^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
. The facts that
![]() $F_\bullet ^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
is an algebra filtration and that
$F_\bullet ^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
is an algebra filtration and that
![]() $dz\in p^*\Omega ({\mathcal {E}}_S)$
then imply that the right-hand side of (3.3.1) belongs to
$dz\in p^*\Omega ({\mathcal {E}}_S)$
then imply that the right-hand side of (3.3.1) belongs to
![]() $F^\delta _{r-1+n_1+\cdots +n_r}\mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)\cdot p^*\Omega ({\mathcal {E}}_S)$
, which implies that
$F^\delta _{r-1+n_1+\cdots +n_r}\mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)\cdot p^*\Omega ({\mathcal {E}}_S)$
, which implies that
![]() $\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
belongs to
$\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
belongs to
![]() $F^\delta _{r+n_1+\cdots +n_r}\mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
. This concludes the proof by induction.
$F^\delta _{r+n_1+\cdots +n_r}\mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
. This concludes the proof by induction.
Corollary 4.4 One has
![]() $\mathcal G\subset A_{{\mathcal {E}}_S}$
.
$\mathcal G\subset A_{{\mathcal {E}}_S}$
.
Proof One has
![]() $O_S={\mathcal {O}}({\mathcal {E}}_S)\subset F^\delta _1{\mathcal {O}}(\tilde {{\mathcal {E}}}_S)\subset F^\delta _\infty {\mathcal {O}}(\tilde {{\mathcal {E}}}_S)$
. Moreover, Lemma 4.2 with
$O_S={\mathcal {O}}({\mathcal {E}}_S)\subset F^\delta _1{\mathcal {O}}(\tilde {{\mathcal {E}}}_S)\subset F^\delta _\infty {\mathcal {O}}(\tilde {{\mathcal {E}}}_S)$
. Moreover, Lemma 4.2 with
![]() $\tilde s=0$
and
$\tilde s=0$
and
![]() $n=1$
implies
$n=1$
implies
![]() $g_1\in F^\delta _1{\mathcal {O}}(\tilde {{\mathcal {E}}}_S) \subset F^\delta _\infty {\mathcal {O}}({\mathcal {E}}_S)$
. Together with Proposition 4.3 and the fact that
$g_1\in F^\delta _1{\mathcal {O}}(\tilde {{\mathcal {E}}}_S) \subset F^\delta _\infty {\mathcal {O}}({\mathcal {E}}_S)$
. Together with Proposition 4.3 and the fact that
![]() $F^\delta _\infty {\mathcal {O}}({\mathcal {E}}_S)$
is an algebra, this implies that
$F^\delta _\infty {\mathcal {O}}({\mathcal {E}}_S)$
is an algebra, this implies that
![]() $\mathcal G\subset F^\delta _\infty {\mathcal {O}}({\mathcal {E}}_S)$
. By [Reference Enriquez and ZerbiniEZ], Theorem C, one has
$\mathcal G\subset F^\delta _\infty {\mathcal {O}}({\mathcal {E}}_S)$
. By [Reference Enriquez and ZerbiniEZ], Theorem C, one has
![]() $F^\delta _\infty {\mathcal {O}}({\mathcal {E}}_S)=A_{{\mathcal {E}}_S}$
, which implies the result.
$F^\delta _\infty {\mathcal {O}}({\mathcal {E}}_S)=A_{{\mathcal {E}}_S}$
, which implies the result.
Proposition 4.3, together with the functional characterization of the algebra
![]() $F_\infty ^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
in Theorem C from [Reference Enriquez and ZerbiniEZ], implies that the functions
$F_\infty ^\delta \mathcal {O}_{hol}(\tilde {{\mathcal {E}}}_S)$
in Theorem C from [Reference Enriquez and ZerbiniEZ], implies that the functions
![]() $\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
have moderate growth at the cusps in the sense explained in [Reference Enriquez and ZerbiniEZ], Section 3.1, and unipotent monodromy in the sense of the introduction.
$\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
have moderate growth at the cusps in the sense explained in [Reference Enriquez and ZerbiniEZ], Section 3.1, and unipotent monodromy in the sense of the introduction.
4.2 The differential algebra
 ${\mathcal {O}}({\mathcal {E}}_0)[g_1]$
${\mathcal {O}}({\mathcal {E}}_0)[g_1]$
Let us set
![]() ${\mathcal {E}}_0:={\mathcal {E}}_{\{pr(0)\}} (={\mathcal {E}}\smallsetminus \{pr(0)\})$
, and
${\mathcal {E}}_0:={\mathcal {E}}_{\{pr(0)\}} (={\mathcal {E}}\smallsetminus \{pr(0)\})$
, and
![]() $O:=O_{\{pr(0)\}} (={\mathcal {O}}({\mathcal {E}}_0))$
. Then O is the algebra of regular functions on
$O:=O_{\{pr(0)\}} (={\mathcal {O}}({\mathcal {E}}_0))$
. Then O is the algebra of regular functions on
![]() ${\mathcal {E}}_0$
, which coincides with the subalgebra of
${\mathcal {E}}_0$
, which coincides with the subalgebra of
![]() $\Lambda $
-invariant functions in
$\Lambda $
-invariant functions in
![]() ${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
. The derivation
${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
. The derivation
![]() $\partial =\partial /\partial z$
of
$\partial =\partial /\partial z$
of
![]() ${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
restricts to a derivation of O.
${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
restricts to a derivation of O.
It is well-known that a linear
![]() $\mathbb C$
-basis of O is
$\mathbb C$
-basis of O is
![]() $\{1,\wp ^{(k)}\,|\,k\geq 0\}$
. It follows from (2.4.4) that an alternative linear
$\{1,\wp ^{(k)}\,|\,k\geq 0\}$
. It follows from (2.4.4) that an alternative linear
![]() $\mathbb C$
-basis of O is
$\mathbb C$
-basis of O is
![]() $\{E_n\,|\,n\in \mathbb Z_{\geq 0}\smallsetminus \{1\}\}$
, where we set
$\{E_n\,|\,n\in \mathbb Z_{\geq 0}\smallsetminus \{1\}\}$
, where we set
![]() $E_0:=1$
. Let us define an algebra filtration on O by the order of poles at
$E_0:=1$
. Let us define an algebra filtration on O by the order of poles at
![]() $pr(0)$
. One then has
$pr(0)$
. One then has
![]() $F_nO:=\sum _{k\in [\![0,n]\!]\smallsetminus \{1\}}\mathbb{C}E_k$
. The associated graded algebra
$F_nO:=\sum _{k\in [\![0,n]\!]\smallsetminus \{1\}}\mathbb{C}E_k$
. The associated graded algebra
![]() $\mathrm {gr}(O)$
is isomorphic to the subalgebra
$\mathrm {gr}(O)$
is isomorphic to the subalgebra
![]() $\mathbb C\oplus Y^2\mathbb C[Y]$
of the polynomial algebra
$\mathbb C\oplus Y^2\mathbb C[Y]$
of the polynomial algebra
![]() $\mathbb C[Y]$
, where Y has degree 1; more precisely, one has
$\mathbb C[Y]$
, where Y has degree 1; more precisely, one has
![]() $\mathrm {gr}_n(O)\simeq \mathbb C\cdot Y^n$
for any
$\mathrm {gr}_n(O)\simeq \mathbb C\cdot Y^n$
for any
![]() $n\in \mathbb Z_{\geq 0}\smallsetminus \{1\}$
, with
$n\in \mathbb Z_{\geq 0}\smallsetminus \{1\}$
, with
![]() $\overline E_n\simeq Y^n$
.
$\overline E_n\simeq Y^n$
.
Let us equip
![]() $\mathbb C[X]$
with the degree filtration, given by
$\mathbb C[X]$
with the degree filtration, given by
![]() $F_n\mathbb C[X]=\oplus _{k\in [\![0,n]\!]}\mathbb CX^k$
for any
$F_n\mathbb C[X]=\oplus _{k\in [\![0,n]\!]}\mathbb CX^k$
for any
![]() $n\geq 0$
; then
$n\geq 0$
; then
![]() $\mathrm {gr}(\mathbb C[X])\simeq \mathbb C[X]$
, where X has degree 1.
$\mathrm {gr}(\mathbb C[X])\simeq \mathbb C[X]$
, where X has degree 1.
Moreover, let us equip the tensor product algebra
![]() $O\otimes \mathbb C[X]$
with the tensor product filtration, so that
$O\otimes \mathbb C[X]$
with the tensor product filtration, so that
![]() $F_n(O\otimes \mathbb C[X])=\sum _{k=0}^n F_kO\otimes F_{n-k}\mathbb C[X]$
. The associated graded algebra
$F_n(O\otimes \mathbb C[X])=\sum _{k=0}^n F_kO\otimes F_{n-k}\mathbb C[X]$
. The associated graded algebra
![]() $\mathrm {gr}(O\otimes \mathbb C[X])$
is then isomorphic to
$\mathrm {gr}(O\otimes \mathbb C[X])$
is then isomorphic to
![]() $\mathrm {gr}(O)\otimes \mathrm {gr}(\mathbb C[X])$
, which is isomorphic to the graded subalgebra
$\mathrm {gr}(O)\otimes \mathrm {gr}(\mathbb C[X])$
, which is isomorphic to the graded subalgebra
![]() $\mathbb C[X]\oplus Y^2\mathbb C[X,Y]$
of
$\mathbb C[X]\oplus Y^2\mathbb C[X,Y]$
of
![]() $\mathbb C[X,Y]$
, where
$\mathbb C[X,Y]$
, where
![]() $X,Y$
have degree 1.
$X,Y$
have degree 1.
Recall that
![]() $g_1=E_1\in {\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
, and
$g_1=E_1\in {\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
, and
![]() $g_1'=-E_2$
. Let
$g_1'=-E_2$
. Let
![]() $O[g_1]$
be the subalgebra of
$O[g_1]$
be the subalgebra of
![]() ${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
generated by O and
${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
generated by O and
![]() $g_1$
. It follows from
$g_1$
. It follows from
![]() $g_1'=-E_2$
that the subalgebra
$g_1'=-E_2$
that the subalgebra
![]() $O[g_1]$
of
$O[g_1]$
of
![]() ${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
is stable under
${\mathcal {O}}_{mer}(\mathbb C,\Lambda )$
is stable under
![]() $\partial $
.
$\partial $
.
Lemma 4.5 One has
![]() $O[g_1] \cap {\mathcal {O}}_{hol}(\mathbb C)=\mathbb C$
.
$O[g_1] \cap {\mathcal {O}}_{hol}(\mathbb C)=\mathbb C$
.
Proof Let us prove inductively on
![]() $d\geq 0$
that if
$d\geq 0$
that if
![]() $a_0,\ldots ,a_d\in O$
and
$a_0,\ldots ,a_d\in O$
and
![]() $\sum _i a_ig_1^i\in {\mathcal {O}}_{hol}(\mathbb C)$
, then
$\sum _i a_ig_1^i\in {\mathcal {O}}_{hol}(\mathbb C)$
, then
![]() $a_0 \in \mathbb C$
and
$a_0 \in \mathbb C$
and
![]() $a_1=\ldots =a_d=0$
. If
$a_1=\ldots =a_d=0$
. If
![]() $d=0$
, then
$d=0$
, then
![]() $a_0 \in O \cap {\mathcal {O}}_{hol}(\mathbb C)=\mathbb C$
, which proves the statement for
$a_0 \in O \cap {\mathcal {O}}_{hol}(\mathbb C)=\mathbb C$
, which proves the statement for
![]() $d=0$
. Assume the statement at step
$d=0$
. Assume the statement at step
![]() $d-1$
and let us prove it at step d. Let
$d-1$
and let us prove it at step d. Let
![]() $a_0,\ldots ,a_d \in O$
be such that
$a_0,\ldots ,a_d \in O$
be such that
![]() $f:=\sum _i a_ig_1^i \in {\mathcal {O}}_{hol}(\mathbb C)$
. Then
$f:=\sum _i a_ig_1^i \in {\mathcal {O}}_{hol}(\mathbb C)$
. Then
 $$ \begin{align*} \sum_{j=0}^{d-1}g_1^j\bigg(\sum_{i>j}a_i\binom{i}{j}(2\pi\mathrm i)^{i-j}\bigg)&=\sum_{(i,j)|j<i}a_i{i \choose j}g_1^j(2\pi\mathrm i)^{i-j}=\sum_i a_i\big((g_1+2\pi\mathrm i)^i-g_1^i\big)\\ &=(T_\tau-id)(f)\in {\mathcal{O}}_{hol}(\mathbb C), \end{align*} $$
$$ \begin{align*} \sum_{j=0}^{d-1}g_1^j\bigg(\sum_{i>j}a_i\binom{i}{j}(2\pi\mathrm i)^{i-j}\bigg)&=\sum_{(i,j)|j<i}a_i{i \choose j}g_1^j(2\pi\mathrm i)^{i-j}=\sum_i a_i\big((g_1+2\pi\mathrm i)^i-g_1^i\big)\\ &=(T_\tau-id)(f)\in {\mathcal{O}}_{hol}(\mathbb C), \end{align*} $$
which by the induction assumption implies that
![]() $\sum _{i>0}a_i(2\pi \mathrm i)^{i} \in \mathbb C$
and for any
$\sum _{i>0}a_i(2\pi \mathrm i)^{i} \in \mathbb C$
and for any
![]() $j=1,\ldots ,d-1$
,
$j=1,\ldots ,d-1$
,
![]() $\sum _{i>j}a_i {i \choose j}(2\pi \mathrm i)^{i-j}=0$
. This implies
$\sum _{i>j}a_i {i \choose j}(2\pi \mathrm i)^{i-j}=0$
. This implies
![]() $a_2=\ldots =a_d=0$
and
$a_2=\ldots =a_d=0$
and
![]() $a_1 \in \mathbb C$
. Then
$a_1 \in \mathbb C$
. Then
![]() $a_0+a_1g_1 \in {\mathcal {O}}_{hol}(\mathbb C)$
. Assume
$a_0+a_1g_1 \in {\mathcal {O}}_{hol}(\mathbb C)$
. Assume
![]() $a_1 \neq 0$
. Since
$a_1 \neq 0$
. Since
![]() $g_1$
has a simple pole at
$g_1$
has a simple pole at
![]() $0$
with residue
$0$
with residue
![]() $1$
, and since
$1$
, and since
![]() $a_0+a_1g_1 \in {\mathcal {O}}_{hol}(\mathbb C)$
,
$a_0+a_1g_1 \in {\mathcal {O}}_{hol}(\mathbb C)$
,
![]() $a_0$
has a simple pole at
$a_0$
has a simple pole at
![]() $0$
with residue
$0$
with residue
![]() $-a_1$
, which contradicts
$-a_1$
, which contradicts
![]() $a_0 \in O$
. Therefore
$a_0 \in O$
. Therefore
![]() $a_1=0$
. Then
$a_1=0$
. Then
![]() $a_0\in {\mathcal {O}}_{hol}(\mathbb C)\cap O=\mathbb C$
, which implies the statement at step d.
$a_0\in {\mathcal {O}}_{hol}(\mathbb C)\cap O=\mathbb C$
, which implies the statement at step d.
Lemma 4.6 The algebra morphism
![]() $O_S\otimes \mathbb C[X]\to O_S[g_1]$
induced by
$O_S\otimes \mathbb C[X]\to O_S[g_1]$
induced by
![]() $f\otimes 1\mapsto f$
for
$f\otimes 1\mapsto f$
for
![]() $f\in O_S$
and
$f\in O_S$
and
![]() $1\otimes X\mapsto g_1$
is an isomorphism.
$1\otimes X\mapsto g_1$
is an isomorphism.
Proof Let P belong to the kernel of this morphism and let d be its degree as a polynomial in X. If
![]() $P\neq 0$
, then there exist
$P\neq 0$
, then there exist
![]() $f_0,\ldots ,f_d\in O_S$
with
$f_0,\ldots ,f_d\in O_S$
with
![]() $f_d\neq 0$
, such that
$f_d\neq 0$
, such that
![]() $P=\sum _{i=0}^d f_i \otimes X^i$
. Then
$P=\sum _{i=0}^d f_i \otimes X^i$
. Then
![]() $\sum _{i=0}^d f_ig_1^i=0$
. Applying
$\sum _{i=0}^d f_ig_1^i=0$
. Applying
![]() $(T_\tau -id)^d$
to this equality, using the invariance of
$(T_\tau -id)^d$
to this equality, using the invariance of
![]() $f_i$
under
$f_i$
under
![]() $T_\tau $
and the relation
$T_\tau $
and the relation
![]() $(T_\tau -id)^d(g_1^i)=\delta _{i,d}(2\pi \mathrm {i})^dd!$
for
$(T_\tau -id)^d(g_1^i)=\delta _{i,d}(2\pi \mathrm {i})^dd!$
for
![]() $i\in [\![0,d]\!]$
, one obtains
$i\in [\![0,d]\!]$
, one obtains
![]() $f_d=0$
, a contradiction.
$f_d=0$
, a contradiction.
Let us equip
![]() $O[g_1]$
with the image
$O[g_1]$
with the image
![]() $F_\bullet (O[g_1])$
of the algebra filtration
$F_\bullet (O[g_1])$
of the algebra filtration
![]() $F_\bullet (O\otimes \mathbb C[X])$
by the algebra isomorphism of Lemma 4.6, specialized to
$F_\bullet (O\otimes \mathbb C[X])$
by the algebra isomorphism of Lemma 4.6, specialized to
![]() $S=\{0\}$
. One then has
$S=\{0\}$
. One then has
 $$ \begin{align} \forall n\geq 0,\quad F_n(O[g_1])=\sum_{k=0}^n (F_kO)\cdot g_1^{n-k}, \quad \mathrm{gr}_n(O[g_1])\simeq \mathbb C\cdot X^n\oplus Y^2\cdot \mathbb C[X,Y]_{n-2}, \end{align} $$
$$ \begin{align} \forall n\geq 0,\quad F_n(O[g_1])=\sum_{k=0}^n (F_kO)\cdot g_1^{n-k}, \quad \mathrm{gr}_n(O[g_1])\simeq \mathbb C\cdot X^n\oplus Y^2\cdot \mathbb C[X,Y]_{n-2}, \end{align} $$
where the notation
![]() $\mathbb C[X,Y]_{n-2}$
indicates the subspace of
$\mathbb C[X,Y]_{n-2}$
indicates the subspace of
![]() $\mathbb C[X,Y]$
of polynomials which are homogeneous of degree
$\mathbb C[X,Y]$
of polynomials which are homogeneous of degree
![]() $n-2$
.
$n-2$
.
Lemma 4.7 If A is an algebra equipped with a filtration
![]() $F_\bullet A$
and if
$F_\bullet A$
and if
![]() $(a_n)_{n\geq 1}$
is a sequence such that
$(a_n)_{n\geq 1}$
is a sequence such that
![]() $a_n\in F_nA$
for
$a_n\in F_nA$
for
![]() $n\geq 1$
, then:
$n\geq 1$
, then:
(a) the sequence
![]() $(b_n)_{n\geq 1}$
of elements of A defined by
$(b_n)_{n\geq 1}$
of elements of A defined by
![]() $1+\sum _{n\geq 1}b_n\alpha ^n=\mathrm {exp}(\sum _{n\geq 1}a_n\alpha ^n)$
(equality in
$1+\sum _{n\geq 1}b_n\alpha ^n=\mathrm {exp}(\sum _{n\geq 1}a_n\alpha ^n)$
(equality in
![]() $A[[\alpha ]])$
) is such that
$A[[\alpha ]])$
) is such that
![]() $b_n\in F_nA$
for any
$b_n\in F_nA$
for any
![]() $n\geq 1$
;
$n\geq 1$
;
(b) one has
![]() $1+\sum _{n\geq 1}\overline b_n= \mathrm {exp}(\sum _{n\geq 1}\overline a_n)$
(equality in
$1+\sum _{n\geq 1}\overline b_n= \mathrm {exp}(\sum _{n\geq 1}\overline a_n)$
(equality in
![]() $\hat \oplus _{n\geq 0}\mathrm {gr}_n(A)$
).
$\hat \oplus _{n\geq 0}\mathrm {gr}_n(A)$
).
The combination of (b) with the specialization of Lemma 4.5 to
![]() $S=\{0\}$
enables one to prove a strengthening of (b), namely the image of the family
$S=\{0\}$
enables one to prove a strengthening of (b), namely the image of the family
![]() $(g_n)_{n\geq 0}$
is a
$(g_n)_{n\geq 0}$
is a
![]() $\mathbb C$
-basis of the cokernel
$\mathbb C$
-basis of the cokernel
![]() $O[g_1]/\partial (O[g_1])$
.
$O[g_1]/\partial (O[g_1])$
.
Proof One has for any
![]() $n\geq 1$
the identity
$n\geq 1$
the identity
 $$ \begin{align*} b_n=\sum_{k\geq 1}\frac{1}{k!}\sum_{\substack{n_1+\cdots+n_k=n,\\(n_1,\ldots,n_k)\in\mathbb Z_{\geq1}^k}}a_{n_1}\cdots a_{n_k}, \end{align*} $$
$$ \begin{align*} b_n=\sum_{k\geq 1}\frac{1}{k!}\sum_{\substack{n_1+\cdots+n_k=n,\\(n_1,\ldots,n_k)\in\mathbb Z_{\geq1}^k}}a_{n_1}\cdots a_{n_k}, \end{align*} $$
which together with the algebra filtration properties implies (a). This identity implies that, for any
![]() $n\geq 1$
,
$n\geq 1$
,
 $$ \begin{align*} \overline b_n=\sum_{k\geq 1}\frac{1}{k!}\sum_{\substack{n_1+\cdots+n_k=n,\\(n_1,\ldots,n_k)\in\mathbb Z_{\geq1}^k}}\overline a_{n_1}\cdots \overline a_{n_k}, \end{align*} $$
$$ \begin{align*} \overline b_n=\sum_{k\geq 1}\frac{1}{k!}\sum_{\substack{n_1+\cdots+n_k=n,\\(n_1,\ldots,n_k)\in\mathbb Z_{\geq1}^k}}\overline a_{n_1}\cdots \overline a_{n_k}, \end{align*} $$
where
![]() $\overline a_i,\overline b_i$
are the classes of
$\overline a_i,\overline b_i$
are the classes of
![]() $a_i,b_i$
in
$a_i,b_i$
in
![]() $\mathrm {gr}_i(A)$
, from which one derives (b).
$\mathrm {gr}_i(A)$
, from which one derives (b).
Lemma 4.8 (a) For every
![]() $n\geq 0$
one has
$n\geq 0$
one has
![]() $g_n\in F_n(O[g_1])$
. Moreover, the degree n polynomial
$g_n\in F_n(O[g_1])$
. Moreover, the degree n polynomial
![]() $(X-Y)^{n-1}(X+(n-1)Y)/n!$
(by convention equal to
$(X-Y)^{n-1}(X+(n-1)Y)/n!$
(by convention equal to
![]() $1$
when
$1$
when
![]() $n=0$
) belongs to
$n=0$
) belongs to
![]() $\mathbb C[X]\oplus Y^2\mathbb C[X,Y]$
and is equal to the image of
$\mathbb C[X]\oplus Y^2\mathbb C[X,Y]$
and is equal to the image of
![]() $\overline g_n\in \mathrm {gr}_n(O[g_1])$
by the isomorphism in (4.2.1).
$\overline g_n\in \mathrm {gr}_n(O[g_1])$
by the isomorphism in (4.2.1).
(b) The family
![]() $(g_n)_{n\geq 0}$
of elements of
$(g_n)_{n\geq 0}$
of elements of
![]() $O[g_1]$
is
$O[g_1]$
is
![]() $\mathbb C$
-linearly independent.
$\mathbb C$
-linearly independent.
(c) There is a direct sum decomposition
in particular,
![]() $\{g_n\,|\,n\geq 0\}$
is a
$\{g_n\,|\,n\geq 0\}$
is a
![]() $\mathbb C$
-basis of the cokernel of the endomorphism
$\mathbb C$
-basis of the cokernel of the endomorphism
![]() $\partial $
of
$\partial $
of
![]() $O[g_1]$
.
$O[g_1]$
.
Proof Equation (2.4.5) implies the identity
 $$ \begin{align*}1+\sum_{n\geq 1}g_n\,\alpha^{n}=\exp\Big((1\otimes X)\,\alpha-\sum_{r\geq2}\frac{(-1)^{r}}{r}\,((E_r-e_r)\otimes 1)\,\alpha^r\Big), \end{align*} $$
$$ \begin{align*}1+\sum_{n\geq 1}g_n\,\alpha^{n}=\exp\Big((1\otimes X)\,\alpha-\sum_{r\geq2}\frac{(-1)^{r}}{r}\,((E_r-e_r)\otimes 1)\,\alpha^r\Big), \end{align*} $$
(equality in
![]() $(O\otimes \mathbb C[X])[[\alpha ]]$
) where for
$(O\otimes \mathbb C[X])[[\alpha ]]$
) where for
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $g_n$
is identified with its image in
$g_n$
is identified with its image in
![]() $O\otimes \mathbb C[X]$
. The first statement in (a) follows from this equality, combined with Lemma 4.7(a) and the relations
$O\otimes \mathbb C[X]$
. The first statement in (a) follows from this equality, combined with Lemma 4.7(a) and the relations
![]() $X\in F_1\mathbb C[X]$
and
$X\in F_1\mathbb C[X]$
and
![]() $E_r-e_r\in F_rO$
for any
$E_r-e_r\in F_rO$
for any
![]() $r\geq 2$
, which imply
$r\geq 2$
, which imply
![]() $1\otimes X\in F_1(O\otimes \mathbb C[X])$
and
$1\otimes X\in F_1(O\otimes \mathbb C[X])$
and
![]() $(E_r-e_r)\otimes 1\in F_r(O\otimes \mathbb C[X])$
for
$(E_r-e_r)\otimes 1\in F_r(O\otimes \mathbb C[X])$
for
![]() $r\geq 2$
. The second statement in (a) follows from Lemma 4.7(b), which implies that
$r\geq 2$
. The second statement in (a) follows from Lemma 4.7(b), which implies that
 $$ \begin{align*}1+\sum_{n\geq 1}\overline g_n &=\exp\Big(\overline{1\otimes X}-\sum_{r\geq2}\frac{(-1)^{r}}{r}\,\overline{(E_r-e_r)\otimes 1}\Big) \\ &=\exp\Big(X-\sum_{r\geq2}\frac{(-1)^{r}}{r}Y^r\Big)=e^{X-Y}(1+Y), \end{align*} $$
$$ \begin{align*}1+\sum_{n\geq 1}\overline g_n &=\exp\Big(\overline{1\otimes X}-\sum_{r\geq2}\frac{(-1)^{r}}{r}\,\overline{(E_r-e_r)\otimes 1}\Big) \\ &=\exp\Big(X-\sum_{r\geq2}\frac{(-1)^{r}}{r}Y^r\Big)=e^{X-Y}(1+Y), \end{align*} $$
(equality in the subalgebra
![]() $\mathbb C[[X]]\oplus Y^2\mathbb C[[X,Y]]$
of
$\mathbb C[[X]]\oplus Y^2\mathbb C[[X,Y]]$
of
![]() $\mathbb C[[X,Y]]$
), which in turn implies that
$\mathbb C[[X,Y]]$
), which in turn implies that
![]() $\overline g_n=(X-Y)^n/n!+Y(X-Y)^{n-1}/(n-1)!=(X-Y)^{n-1}(X+(n-1)Y)/n!$
.
$\overline g_n=(X-Y)^n/n!+Y(X-Y)^{n-1}/(n-1)!=(X-Y)^{n-1}(X+(n-1)Y)/n!$
.
(b) If
![]() $\sum _n\lambda _ng_n=0$
is a nontrivial linear dependence relation, let
$\sum _n\lambda _ng_n=0$
is a nontrivial linear dependence relation, let
![]() $i:=\mathrm {max}\{i|\lambda _i\neq 0\}$
. Then
$i:=\mathrm {max}\{i|\lambda _i\neq 0\}$
. Then
![]() $0=\sum _n\lambda _ng_n\in F_i(O[g_1])$
, and the image of this element in
$0=\sum _n\lambda _ng_n\in F_i(O[g_1])$
, and the image of this element in
![]() $\mathrm {gr}_i(O[g_1])$
is
$\mathrm {gr}_i(O[g_1])$
is
![]() $\lambda _i\overline {g_i}$
, which is nonzero, this yielding a contradiction.
$\lambda _i\overline {g_i}$
, which is nonzero, this yielding a contradiction.
(c) Let D be the endomorphism of
![]() $O\otimes \mathbb C[X]$
defined by
$O\otimes \mathbb C[X]$
defined by
![]() $D(f\otimes P):=\partial f\otimes P-fE_2\otimes P'$
. Then D is a derivation of
$D(f\otimes P):=\partial f\otimes P-fE_2\otimes P'$
. Then D is a derivation of
![]() $O\otimes \mathbb C[X]$
, which is interwined with
$O\otimes \mathbb C[X]$
, which is interwined with
![]() $\partial $
under the specialization of the isomorphism from Lemma 4.6 to
$\partial $
under the specialization of the isomorphism from Lemma 4.6 to
![]() $S=\{0\}$
.
$S=\{0\}$
.
The derivation
![]() $\partial $
of O is of filtration degree 1, i.e.,
$\partial $
of O is of filtration degree 1, i.e.,
![]() $\partial (F_kO)\subset F_{k+1}O$
for any
$\partial (F_kO)\subset F_{k+1}O$
for any
![]() $k\geq 0$
. The associated graded endomorphism
$k\geq 0$
. The associated graded endomorphism
![]() $\mathrm {gr}(\partial )$
is then a degree 1 derivation of
$\mathrm {gr}(\partial )$
is then a degree 1 derivation of
![]() $\mathbb C\oplus Y^2\mathbb C[Y]$
. The image of the derivation
$\mathbb C\oplus Y^2\mathbb C[Y]$
. The image of the derivation
![]() $Y^2\partial /\partial Y$
of
$Y^2\partial /\partial Y$
of
![]() $\mathbb C[Y]$
is contained in
$\mathbb C[Y]$
is contained in
![]() $Y^2\mathbb C[Y]$
, therefore
$Y^2\mathbb C[Y]$
, therefore
![]() $Y^2\partial /\partial Y$
induces a derivation of
$Y^2\partial /\partial Y$
induces a derivation of
![]() $\mathbb C\oplus Y^2\mathbb C[Y]$
of degree 1, which can be seen to coincide with
$\mathbb C\oplus Y^2\mathbb C[Y]$
of degree 1, which can be seen to coincide with
![]() $\mathrm {gr}(\partial )$
. One deduces from this that the derivation
$\mathrm {gr}(\partial )$
. One deduces from this that the derivation
![]() $\partial \otimes \mathrm {id}$
of
$\partial \otimes \mathrm {id}$
of
![]() $O \otimes \mathbb C[X]$
is of filtration degree 1, and that its associated graded is the derivation
$O \otimes \mathbb C[X]$
is of filtration degree 1, and that its associated graded is the derivation
![]() $Y^2 \partial /\partial Y$
of
$Y^2 \partial /\partial Y$
of
![]() $\mathbb C[X] \oplus Y^2 \mathbb C[X,Y]$
.
$\mathbb C[X] \oplus Y^2 \mathbb C[X,Y]$
.
The endomorphism
![]() $f\otimes P\mapsto -E_2f\otimes P'$
is a derivation of
$f\otimes P\mapsto -E_2f\otimes P'$
is a derivation of
![]() $O\otimes \mathbb C[X]$
, which is also of filtration degree 1, as
$O\otimes \mathbb C[X]$
, which is also of filtration degree 1, as
![]() $E_2$
has filtration degree 2 and
$E_2$
has filtration degree 2 and
![]() $P\mapsto P'$
has filtration degree
$P\mapsto P'$
has filtration degree
![]() $-1$
. The associated graded of the endomorphism
$-1$
. The associated graded of the endomorphism
![]() $f\mapsto E_2f$
of O (resp.
$f\mapsto E_2f$
of O (resp.
![]() $P\mapsto P'$
of
$P\mapsto P'$
of
![]() $\mathbb C[X]$
) is the endomorphism
$\mathbb C[X]$
) is the endomorphism
![]() $f\mapsto Y^2f$
of
$f\mapsto Y^2f$
of
![]() $\mathbb C \oplus Y^2\mathbb C[Y]$
(resp.
$\mathbb C \oplus Y^2\mathbb C[Y]$
(resp.
![]() $\partial /\partial X$
of
$\partial /\partial X$
of
![]() $\mathbb C[X]$
), therefore the associated graded of
$\mathbb C[X]$
), therefore the associated graded of
![]() $f\otimes P\mapsto -E_2f\otimes P'$
is the degree 1 derivation of
$f\otimes P\mapsto -E_2f\otimes P'$
is the degree 1 derivation of
![]() $\mathbb C[X]\oplus Y^2\mathbb C[X,Y]$
given by
$\mathbb C[X]\oplus Y^2\mathbb C[X,Y]$
given by
![]() $-Y^2\partial /\partial X$
.
$-Y^2\partial /\partial X$
.
It follows that D has filtration degree 1, and that its associated graded is the derivation of
![]() $\mathbb C[X] \oplus Y^2\mathbb C[X,Y]$
induced by the derivation
$\mathbb C[X] \oplus Y^2\mathbb C[X,Y]$
induced by the derivation
![]() $Y^2({\partial \over \partial Y}-{\partial \over \partial X})$
of
$Y^2({\partial \over \partial Y}-{\partial \over \partial X})$
of
![]() $\mathbb C[X,Y]$
.
$\mathbb C[X,Y]$
.
We now prove by induction on
![]() $k\geq 0$
the equality of subspaces of
$k\geq 0$
the equality of subspaces of
![]() $O[g_1]$
$O[g_1]$
One has
![]() $F_0(O[g_1])=\mathbb C$
and
$F_0(O[g_1])=\mathbb C$
and
![]() $F_1(O[g_1])=\mathrm {Span}_{\mathbb C}(1,g_1)$
, which implies (4.2.3) for
$F_1(O[g_1])=\mathrm {Span}_{\mathbb C}(1,g_1)$
, which implies (4.2.3) for
![]() $k=0$
. Assume
$k=0$
. Assume
![]() $k>0$
and
$k>0$
and
![]() $F_{k}(O[g_1])=\partial (F_{k-1}(O[g_1]))+\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k})$
, and let us show (4.2.3). The inclusion of the right-hand side in the left-hand side is obvious, so one has to show that this inclusion is an equality.
$F_{k}(O[g_1])=\partial (F_{k-1}(O[g_1]))+\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k})$
, and let us show (4.2.3). The inclusion of the right-hand side in the left-hand side is obvious, so one has to show that this inclusion is an equality.
Recall that the space
![]() $\partial (F_k(O[g_1]))$
is a subspace of
$\partial (F_k(O[g_1]))$
is a subspace of
![]() $F_{k+1}(O[g_1])$
. It follows from the commutativity of
$F_{k+1}(O[g_1])$
. It follows from the commutativity of

and from the surjectivity of
![]() $F_k(O[g_1])\to \mathrm {gr}_k(O[g_1])$
that the image of this subspace in
$F_k(O[g_1])\to \mathrm {gr}_k(O[g_1])$
that the image of this subspace in
![]() $\mathrm {gr}_{k+1}(O[g_1])$
is equal to the image of
$\mathrm {gr}_{k+1}(O[g_1])$
is equal to the image of
![]() $\mathrm {gr}_k(\partial ) : \mathrm {gr}_k(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])$
, which is identified with the map
$\mathrm {gr}_k(\partial ) : \mathrm {gr}_k(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])$
, which is identified with the map
The image of (4.2.4) is obviously contained in
![]() $Y^2\cdot \mathbb C[X,Y]_{k-1}$
, which induces a linear map
$Y^2\cdot \mathbb C[X,Y]_{k-1}$
, which induces a linear map
The kernel of the linear endomorphism
![]() $Y^2({\partial \over \partial X}-{\partial \over \partial Y})$
of
$Y^2({\partial \over \partial X}-{\partial \over \partial Y})$
of
![]() $\mathbb C[X,Y]$
is
$\mathbb C[X,Y]$
is
![]() $\mathbb C[X+Y]$
, which implies that the kernel of the linear map
$\mathbb C[X+Y]$
, which implies that the kernel of the linear map
![]() $Y^2({\partial \over \partial X}-{\partial \over \partial Y}) : \mathbb C[X,Y]_k\to \mathbb C[X,Y]_{k+1}$
is the one-dimensional vector space
$Y^2({\partial \over \partial X}-{\partial \over \partial Y}) : \mathbb C[X,Y]_k\to \mathbb C[X,Y]_{k+1}$
is the one-dimensional vector space
![]() $\mathbb C\cdot (X+Y)^k$
. The kernel of (4.2.5) is the intersection of this vector space with the source of (4.2.5), which is zero as the coefficient of
$\mathbb C\cdot (X+Y)^k$
. The kernel of (4.2.5) is the intersection of this vector space with the source of (4.2.5), which is zero as the coefficient of
![]() $YX^{k-1}$
in
$YX^{k-1}$
in
![]() $(X+Y)^k$
is nonzero; this implies that the map (4.2.5) is injective. The source and target of (4.2.5) both have dimension k; the equality of these dimensions, together with the injectivity of (4.2.5), implies that (4.2.5) is a linear isomorphism. All this implies that the image of (4.2.4) is equal to
$(X+Y)^k$
is nonzero; this implies that the map (4.2.5) is injective. The source and target of (4.2.5) both have dimension k; the equality of these dimensions, together with the injectivity of (4.2.5), implies that (4.2.5) is a linear isomorphism. All this implies that the image of (4.2.4) is equal to
![]() $Y^2\cdot \mathbb C[X,Y]_{k-1}$
, therefore that the image of
$Y^2\cdot \mathbb C[X,Y]_{k-1}$
, therefore that the image of
![]() $\partial (F_k(O[g_1]))$
by
$\partial (F_k(O[g_1]))$
by
![]() $F_{k+1}(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])\simeq \mathbb CX^{k+1}\oplus Y^2\cdot \mathbb C[X,Y]_{k-1}$
is
$F_{k+1}(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])\simeq \mathbb CX^{k+1}\oplus Y^2\cdot \mathbb C[X,Y]_{k-1}$
is
![]() $Y^2\cdot \mathbb C[X,Y]_{k-1}$
.
$Y^2\cdot \mathbb C[X,Y]_{k-1}$
.
On the other hand,
![]() $\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_k)\subset F_k(O[g_1])$
, which implies that the image of
$\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_k)\subset F_k(O[g_1])$
, which implies that the image of
![]() $\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k+1})$
under
$\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k+1})$
under
![]() $F_{k+1}(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])$
is
$F_{k+1}(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])$
is
![]() $\mathbb C\,\overline g_{k+1}$
, whose image in
$\mathbb C\,\overline g_{k+1}$
, whose image in
![]() $\mathbb CX^{k+1}\oplus Y^2\cdot \mathbb C[X,Y]_{k-1}$
is given by (a).
$\mathbb CX^{k+1}\oplus Y^2\cdot \mathbb C[X,Y]_{k-1}$
is given by (a).
Then the image of
![]() $\partial (F_k(O[g_1]))+\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k+1})$
under
$\partial (F_k(O[g_1]))+\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k+1})$
under
![]() $F_{k+1}(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])$
is the sum of the images of
$F_{k+1}(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])$
is the sum of the images of
![]() $\partial (F_k(O[g_1]))$
and
$\partial (F_k(O[g_1]))$
and
![]() $\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k+1})$
under this map, which is equal to the sum
$\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k+1})$
under this map, which is equal to the sum
![]() $Y^2\cdot \mathbb C[X,Y]_{k-1}+\mathbb C(X-Y)^{k}(X+kY)/(k+1)!$
, that can be simplified into
$Y^2\cdot \mathbb C[X,Y]_{k-1}+\mathbb C(X-Y)^{k}(X+kY)/(k+1)!$
, that can be simplified into
![]() $\mathbb C\cdot X^k\oplus Y^2\cdot \mathbb C[X,Y]_{k-1}\simeq \mathrm {gr}_{k+1}(O[g_1])$
.
$\mathbb C\cdot X^k\oplus Y^2\cdot \mathbb C[X,Y]_{k-1}\simeq \mathrm {gr}_{k+1}(O[g_1])$
.
It follows that the image of
![]() $\partial (F_k(O[g_1]))+\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k+1})$
under the projection
$\partial (F_k(O[g_1]))+\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k+1})$
under the projection
![]() $F_{k+1}(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])$
is equal to its target. The space
$F_{k+1}(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])$
is equal to its target. The space
![]() $\partial (F_k(O[g_1]))+\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k+1})$
also contains
$\partial (F_k(O[g_1]))+\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k+1})$
also contains
![]() $\partial (F_{k-1}(O[g_1]))+\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k})$
, which by the induction hypothesis is equal to
$\partial (F_{k-1}(O[g_1]))+\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k})$
, which by the induction hypothesis is equal to
![]() $F_k(O[g_1])$
, and therefore also to the kernel of the projection
$F_k(O[g_1])$
, and therefore also to the kernel of the projection
![]() $F_{k+1}(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])$
. All this implies the equality
$F_{k+1}(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])$
. All this implies the equality
![]() $\partial (F_k(O[g_1]))+\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k+1})=F_{k+1}(O[g_1])$
, which proves the induction step. This proves (4.2.3) for any
$\partial (F_k(O[g_1]))+\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k+1})=F_{k+1}(O[g_1])$
, which proves the induction step. This proves (4.2.3) for any
![]() $k\geq 0$
.
$k\geq 0$
.
Let us now prove by induction on
![]() $k\geq 0$
the equality of subspaces of
$k\geq 0$
the equality of subspaces of
![]() $F_{k+1}(O[g_1])$
$F_{k+1}(O[g_1])$
One has
![]() $F_0(O[g_1])=\mathbb C$
hence
$F_0(O[g_1])=\mathbb C$
hence
![]() $\partial (F_0(O[g_1]))=0$
, which implies (4.2.6) for
$\partial (F_0(O[g_1]))=0$
, which implies (4.2.6) for
![]() $k=0$
. Assume
$k=0$
. Assume
![]() $k>0$
and
$k>0$
and
![]() $\partial (F_{k-1}(O[g_1]))\cap \mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k})=\{0\}$
, and let us show (4.2.6). Let
$\partial (F_{k-1}(O[g_1]))\cap \mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k})=\{0\}$
, and let us show (4.2.6). Let
![]() $P\in F_k(O[g_1])$
,
$P\in F_k(O[g_1])$
,
![]() $(\lambda _i)_{i\in [0,k+1]}\in \mathbb C^{k+2}$
be such that
$(\lambda _i)_{i\in [0,k+1]}\in \mathbb C^{k+2}$
be such that
![]() $\partial (P)=\sum _i\lambda _i g_i$
. The image of this equality under the projection
$\partial (P)=\sum _i\lambda _i g_i$
. The image of this equality under the projection
![]() $F_{k+1}(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])$
is
$F_{k+1}(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])$
is
![]() $\lambda _{k+1}\overline {g_{k+1}}=\mathrm {gr}_k(\partial )(\overline P)$
, where
$\lambda _{k+1}\overline {g_{k+1}}=\mathrm {gr}_k(\partial )(\overline P)$
, where
![]() $\overline P$
is the image of P in
$\overline P$
is the image of P in
![]() $\mathrm {gr}_k(O[g_1])$
. The map
$\mathrm {gr}_k(O[g_1])$
. The map
![]() $\mathrm {gr}_k(\partial ) : \mathrm {gr}_k(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])$
is injective (as this maps can be identified with (4.2.5) which has been proved to be injective), and its image does not contain
$\mathrm {gr}_k(\partial ) : \mathrm {gr}_k(O[g_1])\to \mathrm {gr}_{k+1}(O[g_1])$
is injective (as this maps can be identified with (4.2.5) which has been proved to be injective), and its image does not contain
![]() $\overline {g_{k+1}}$
(as this image has been proved to be identified to
$\overline {g_{k+1}}$
(as this image has been proved to be identified to
![]() $Y^2\mathbb C[X,Y]_{k-1}$
and in view of the identification of
$Y^2\mathbb C[X,Y]_{k-1}$
and in view of the identification of
![]() $\overline {g_{k+1}}$
in (a)). It follows that
$\overline {g_{k+1}}$
in (a)). It follows that
![]() $\lambda _{k+1}=0$
and
$\lambda _{k+1}=0$
and
![]() $\overline P=0$
, therefore in the equality
$\overline P=0$
, therefore in the equality
![]() $\partial (P)=\sum _i\lambda _i g_i$
the left-hand side belongs to
$\partial (P)=\sum _i\lambda _i g_i$
the left-hand side belongs to
![]() $\partial (F_{k-1}(O[g_1]))$
and the right-hand side to
$\partial (F_{k-1}(O[g_1]))$
and the right-hand side to
![]() $\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k})$
, which by the induction assumption implies
$\mathrm {Span}_{\mathbb C}(1,g_1,\ldots ,g_{k})$
, which by the induction assumption implies
![]() $\partial (P)=0$
and
$\partial (P)=0$
and
![]() $\lambda _0=\ldots =\lambda _k=0$
. This proves the induction step, therefore (4.2.6) holds for any
$\lambda _0=\ldots =\lambda _k=0$
. This proves the induction step, therefore (4.2.6) holds for any
![]() $k\geq 0$
.
$k\geq 0$
.
Then
 $$ \begin{align} \nonumber O[g_1] &=\sum_{k \geq 0}F_{k+1}(O[g_1]) =\sum_{k \geq 0}\partial(F_k(O[g_1]))+\mathrm{Span}_{\mathbb C}(1,g_1,\ldots,g_{k+1}) \\ &\nonumber =\sum_{k \geq 0}\partial(F_k(O[g_1])) +\sum_{k \geq 0}\mathrm{Span}_{\mathbb C}(1,g_1,\ldots,g_{k+1}) \\ &=\partial \left(\sum_{k \geq 0}F_k(O[g_1])\right)+ \mathrm{Span}_{\mathbb C}(g_i,i\geq 0) \nonumber\\ & =\partial(O[g_1]) +\mathrm{Span}_{\mathbb C}(g_i,i\geq0), \end{align} $$
$$ \begin{align} \nonumber O[g_1] &=\sum_{k \geq 0}F_{k+1}(O[g_1]) =\sum_{k \geq 0}\partial(F_k(O[g_1]))+\mathrm{Span}_{\mathbb C}(1,g_1,\ldots,g_{k+1}) \\ &\nonumber =\sum_{k \geq 0}\partial(F_k(O[g_1])) +\sum_{k \geq 0}\mathrm{Span}_{\mathbb C}(1,g_1,\ldots,g_{k+1}) \\ &=\partial \left(\sum_{k \geq 0}F_k(O[g_1])\right)+ \mathrm{Span}_{\mathbb C}(g_i,i\geq 0) \nonumber\\ & =\partial(O[g_1]) +\mathrm{Span}_{\mathbb C}(g_i,i\geq0), \end{align} $$
where the second equality follows from (4.2.3).
For any
![]() $k,l \geq 0$
, one has
$k,l \geq 0$
, one has
 $$ \begin{align*}\partial(F_kO[g_1]) &\cap \mathrm{Span}_{\mathbb C}(1,g_1,\ldots,g_{l+1}) \subset \partial(F_{\mathrm{max}(k,l)}O[g_1]) \\ &\cap \mathrm{Span}_{\mathbb C}(1,g_1,\ldots,g_{\mathrm{max}(k,l)+1})=0, \end{align*} $$
$$ \begin{align*}\partial(F_kO[g_1]) &\cap \mathrm{Span}_{\mathbb C}(1,g_1,\ldots,g_{l+1}) \subset \partial(F_{\mathrm{max}(k,l)}O[g_1]) \\ &\cap \mathrm{Span}_{\mathbb C}(1,g_1,\ldots,g_{\mathrm{max}(k,l)+1})=0, \end{align*} $$
where the last equality follows from (4.2.6). This implies
Then
 $$ \begin{align} \nonumber\partial(O[g_1]) \cap \mathrm{Span}_{\mathbb C}(g_i,i\geq 0) &=(\cup_{k \geq 0}\partial(F_kO[g_1])) \cap (\cup_{l \geq 0}\mathrm{Span}_{\mathbb C}(1,g_1,\ldots,g_{l+1}) \\ & =\cup_{k,l \geq 0} \partial(F_kO[g_1]) \cap \mathrm{Span}_{\mathbb C}(1,g_1,\ldots,g_{l+1})=0, \end{align} $$
$$ \begin{align} \nonumber\partial(O[g_1]) \cap \mathrm{Span}_{\mathbb C}(g_i,i\geq 0) &=(\cup_{k \geq 0}\partial(F_kO[g_1])) \cap (\cup_{l \geq 0}\mathrm{Span}_{\mathbb C}(1,g_1,\ldots,g_{l+1}) \\ & =\cup_{k,l \geq 0} \partial(F_kO[g_1]) \cap \mathrm{Span}_{\mathbb C}(1,g_1,\ldots,g_{l+1})=0, \end{align} $$
where the last equality follows from (4.2.8).
The statement then follows from the combination of (4.2.7) and (4.2.9).
4.3 The differential algebra
 ${\mathcal {O}}({\mathcal {E}}_S)[g_1]$
${\mathcal {O}}({\mathcal {E}}_S)[g_1]$
Let us denote by
![]() $\mathbb C({\mathcal {E}})$
the field of rational functions on
$\mathbb C({\mathcal {E}})$
the field of rational functions on
![]() ${\mathcal {E}}$
. As an algebra, it can be identified with the algebra of
${\mathcal {E}}$
. As an algebra, it can be identified with the algebra of
![]() $\Lambda $
-invariant meromorphic functions on
$\Lambda $
-invariant meromorphic functions on
![]() $\mathbb C$
. Recall that, for
$\mathbb C$
. Recall that, for
![]() $a\in \mathbb C$
, the translation
$a\in \mathbb C$
, the translation
![]() $T_a$
is an automorphism of the algebra of meromorphic functions on
$T_a$
is an automorphism of the algebra of meromorphic functions on
![]() $\mathbb C$
; it induces an automorphism of
$\mathbb C$
; it induces an automorphism of
![]() $\mathbb C({\mathcal {E}})$
, which moreover depends only on the class of a in
$\mathbb C({\mathcal {E}})$
, which moreover depends only on the class of a in
![]() ${\mathcal {E}}$
.
${\mathcal {E}}$
.
Recall the map
![]() $s\mapsto \tilde s$
from Definition 2.10(a).
$s\mapsto \tilde s$
from Definition 2.10(a).
Lemma 4.9 (a) For any
![]() $s\in S$
, one has
$s\in S$
, one has
![]() $(T_{\tilde s}-id)(g_1)\in O_S$
.
$(T_{\tilde s}-id)(g_1)\in O_S$
.
(b)
![]() $O_S=\sum _{s\in S}T_s(O)+\sum _{s\in S\smallsetminus \{pr(0)\}}\mathbb C\cdot (T_{\tilde s}-id)(g_1)$
(equality of subspaces of
$O_S=\sum _{s\in S}T_s(O)+\sum _{s\in S\smallsetminus \{pr(0)\}}\mathbb C\cdot (T_{\tilde s}-id)(g_1)$
(equality of subspaces of
![]() $\mathbb C({\mathcal {E}})$
).
$\mathbb C({\mathcal {E}})$
).
Proof The relations
![]() $T_1g_1=g_1$
and
$T_1g_1=g_1$
and
![]() $T_\tau g_1=g_1+2\pi \mathrm {i}$
, together with the commutativity of the various
$T_\tau g_1=g_1+2\pi \mathrm {i}$
, together with the commutativity of the various
![]() $T_a$
,
$T_a$
,
![]() $a\in \mathbb C$
, implies that for any
$a\in \mathbb C$
, implies that for any
![]() $s\in S$
the function
$s\in S$
the function
![]() $(T_{\tilde s}-1)(g_1)$
is
$(T_{\tilde s}-1)(g_1)$
is
![]() $\Lambda $
-invariant. It has simple poles at
$\Lambda $
-invariant. It has simple poles at
![]() $0$
and s, which implies that it belongs to
$0$
and s, which implies that it belongs to
![]() $O_S$
, which proves (a). One clearly has
$O_S$
, which proves (a). One clearly has
![]() $T_s(O)\subset O_S$
for any
$T_s(O)\subset O_S$
for any
![]() $s\in S$
, so that (a) implies the inclusion
$s\in S$
, so that (a) implies the inclusion
![]() $O_S\supset \sum _{s\in S}T_s(O)+\sum _{s\in S\smallsetminus \{pr(0)\}}\mathbb C\cdot (T_{\tilde s}-1)(g_1)$
. If now
$O_S\supset \sum _{s\in S}T_s(O)+\sum _{s\in S\smallsetminus \{pr(0)\}}\mathbb C\cdot (T_{\tilde s}-1)(g_1)$
. If now
![]() $f\in O_S$
, let
$f\in O_S$
, let
![]() $(f_s)_{s\in S}$
be the collection where
$(f_s)_{s\in S}$
be the collection where
![]() $f_s\in \mathbb C((z-\tilde s))$
is the local expansion of f at
$f_s\in \mathbb C((z-\tilde s))$
is the local expansion of f at
![]() $\tilde s$
. The map
$\tilde s$
. The map
![]() $O\to \mathbb C((z))\to \mathbb C((z))/z^{-1}\mathbb C[[z]]$
is surjective, so for any
$O\to \mathbb C((z))\to \mathbb C((z))/z^{-1}\mathbb C[[z]]$
is surjective, so for any
![]() $s\in S$
one can find
$s\in S$
one can find
![]() $o_s\in O$
whose image by this map coincides with the image of
$o_s\in O$
whose image by this map coincides with the image of
![]() $f_s$
by the map
$f_s$
by the map
![]() $\mathbb C((z-\tilde s))\simeq \mathbb C((z))\to \mathbb C((z))/z^{-1}\mathbb C[[z]]$
. Then
$\mathbb C((z-\tilde s))\simeq \mathbb C((z))\to \mathbb C((z))/z^{-1}\mathbb C[[z]]$
. Then
![]() $g:=f-\sum _{s\in S}T_s(o_s)$
belongs to
$g:=f-\sum _{s\in S}T_s(o_s)$
belongs to
![]() $O_S$
and has at most simple poles at S. Then
$O_S$
and has at most simple poles at S. Then
![]() $g-\sum _{s\in S\smallsetminus pr(0)}\mathrm {res}_s(g\cdot dz)\cdot (T_{\tilde s}-id)(g_1)$
belongs to
$g-\sum _{s\in S\smallsetminus pr(0)}\mathrm {res}_s(g\cdot dz)\cdot (T_{\tilde s}-id)(g_1)$
belongs to
![]() $O_S$
and is regular on
$O_S$
and is regular on
![]() $S\smallsetminus pr(0)$
; hence it belongs to O and has at most a simple pole at
$S\smallsetminus pr(0)$
; hence it belongs to O and has at most a simple pole at
![]() $pr(0)$
, which implies that it is constant. This proves the desired opposite inclusion.
$pr(0)$
, which implies that it is constant. This proves the desired opposite inclusion.
Recall that
![]() ${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
is the algebra of meromorphic functions on
${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
is the algebra of meromorphic functions on
![]() $\mathbb C$
with set of poles contained in
$\mathbb C$
with set of poles contained in
![]() $pr^{-1}(S)$
. Then
$pr^{-1}(S)$
. Then
![]() $\Lambda $
acts by translation on
$\Lambda $
acts by translation on
![]() ${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
, and
${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
, and
![]() $O_S={\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))^\Lambda $
. The operator
$O_S={\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))^\Lambda $
. The operator
![]() $\partial =d/dz$
defines a derivation on
$\partial =d/dz$
defines a derivation on
![]() ${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
, which restricts to a derivation of
${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
, which restricts to a derivation of
![]() $O_S$
.
$O_S$
.
Consider the subalgebra
![]() $O_S[g_1]$
of
$O_S[g_1]$
of
![]() ${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
. Then
${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
. Then
![]() $\partial (g_1)=-E_2\in O_S$
implies that
$\partial (g_1)=-E_2\in O_S$
implies that
![]() $O_S[g_1]$
is stable under
$O_S[g_1]$
is stable under
![]() $\partial $
.
$\partial $
.
Lemma 4.10 Let
![]() $a\in \mathbb C\smallsetminus \Lambda $
.
$a\in \mathbb C\smallsetminus \Lambda $
.
(a) If
![]() $f\in {\mathcal {O}}_{mer}(\mathbb C, \Lambda \cup (a+\Lambda ))$
is such that
$f\in {\mathcal {O}}_{mer}(\mathbb C, \Lambda \cup (a+\Lambda ))$
is such that
![]() $T_1(f)=f$
and
$T_1(f)=f$
and
![]() $(T_\tau -id)(f) \in O[g_1]+T_a(O[g_1])$
, then
$(T_\tau -id)(f) \in O[g_1]+T_a(O[g_1])$
, then
![]() $f \in O[g_1]+T_a(O[g_1])$
.
$f \in O[g_1]+T_a(O[g_1])$
.
(b) If
![]() $f\in {\mathcal {O}}_{mer}(\mathbb C, \Lambda \cup (a+\Lambda ))$
is such that
$f\in {\mathcal {O}}_{mer}(\mathbb C, \Lambda \cup (a+\Lambda ))$
is such that
![]() $T_1(f)=f$
and that for some
$T_1(f)=f$
and that for some
![]() $n\geq 1$
one has
$n\geq 1$
one has
![]() $(T_\tau -id)^n(f) \in O[g_1]+T_a(O[g_1])$
, then
$(T_\tau -id)^n(f) \in O[g_1]+T_a(O[g_1])$
, then
![]() $f \in O[g_1]+T_a(O[g_1])$
.
$f \in O[g_1]+T_a(O[g_1])$
.
(c) For any
![]() $n\geq 0$
, one has
$n\geq 0$
, one has
Proof (a) The automorphism
![]() $T_\tau $
of
$T_\tau $
of
![]() ${\mathcal {O}}_{mer}(\mathbb C,\Lambda \cup (a+\Lambda ))$
restricts to automorphisms of the subalgebras
${\mathcal {O}}_{mer}(\mathbb C,\Lambda \cup (a+\Lambda ))$
restricts to automorphisms of the subalgebras
![]() $O[g_1]$
and
$O[g_1]$
and
![]() $T_a(O[g_1])$
, therefore to an automorphism of the vector subspace
$T_a(O[g_1])$
, therefore to an automorphism of the vector subspace
![]() $O[g_1]+T_a(O[g_1])$
.
$O[g_1]+T_a(O[g_1])$
.
The O-algebra morphism
![]() $O[X]\to O[g_1]$
induced by
$O[X]\to O[g_1]$
induced by
![]() $X \mapsto g_1$
intertwines the linear endomorphism
$X \mapsto g_1$
intertwines the linear endomorphism
![]() $T_\tau -id$
of
$T_\tau -id$
of
![]() $O[g_1]$
with the linear endomorphism
$O[g_1]$
with the linear endomorphism
![]() $\mathrm {exp}(2\pi \mathrm {i}\partial _X)-1$
of
$\mathrm {exp}(2\pi \mathrm {i}\partial _X)-1$
of
![]() $O[X]$
, where
$O[X]$
, where
![]() $\partial $
is the derivation of
$\partial $
is the derivation of
![]() $O[X]$
given by
$O[X]$
given by
![]() $O\mapsto 0$
and
$O\mapsto 0$
and
![]() $X\mapsto 1$
. On the other hand,
$X\mapsto 1$
. On the other hand,
![]() $\mathrm {exp}(2\pi \mathrm {i}\partial _X)-1={\mathrm {exp}(2\pi \mathrm {i}\partial _X)-1\over \partial _X}\circ \partial _X$
, where
$\mathrm {exp}(2\pi \mathrm {i}\partial _X)-1={\mathrm {exp}(2\pi \mathrm {i}\partial _X)-1\over \partial _X}\circ \partial _X$
, where
![]() ${\mathrm {exp}(2\pi \mathrm {i}\partial _X)-1\over \partial _X}$
is a linear automorphism of
${\mathrm {exp}(2\pi \mathrm {i}\partial _X)-1\over \partial _X}$
is a linear automorphism of
![]() $O[X]$
as
$O[X]$
as
![]() $\partial _X$
is locally nilpotent, and
$\partial _X$
is locally nilpotent, and
![]() $\partial _X$
is surjective. It follows that the linear endomorphism
$\partial _X$
is surjective. It follows that the linear endomorphism
![]() $\mathrm {exp}(2\pi \mathrm {i}\partial _X)-1$
of
$\mathrm {exp}(2\pi \mathrm {i}\partial _X)-1$
of
![]() $O[X]$
is surjective. It follows from this surjectivity, from the interwtining of this operator with
$O[X]$
is surjective. It follows from this surjectivity, from the interwtining of this operator with
![]() $T_\tau -id$
and from the surjectivity of the map
$T_\tau -id$
and from the surjectivity of the map
![]() $O[X]\to O[g_1]$
that the linear endomorphism
$O[X]\to O[g_1]$
that the linear endomorphism
![]() $T_\tau -id$
of
$T_\tau -id$
of
![]() $O[g_1]$
is surjective. This implies the surjectivity of the linear endomorphism
$O[g_1]$
is surjective. This implies the surjectivity of the linear endomorphism
![]() $T_\tau -id$
of
$T_\tau -id$
of
![]() $T_a(O[g_1])$
, and therefore that of the linear endomorphism
$T_a(O[g_1])$
, and therefore that of the linear endomorphism
![]() $T_\tau -id$
of
$T_\tau -id$
of
![]() $O[g_1]+T_a(O[g_1])$
.
$O[g_1]+T_a(O[g_1])$
.
Let now f be as in the (a). It follows from the surjectivity of the linear endomorphism
![]() $T_\tau -id$
of
$T_\tau -id$
of
![]() $O[g_1]+T_a(O[g_1])$
that there exists
$O[g_1]+T_a(O[g_1])$
that there exists
![]() $\tilde f \in O[g_1]+T_a(O[g_1])$
, such that
$\tilde f \in O[g_1]+T_a(O[g_1])$
, such that
![]() $(T_\tau -id)(\tilde f)=(T_\tau -id)(f)$
(equality in
$(T_\tau -id)(\tilde f)=(T_\tau -id)(f)$
(equality in
![]() $O[g_1]+T_a(O[g_1])$
). Then
$O[g_1]+T_a(O[g_1])$
). Then
![]() $f-\tilde f$
belongs to
$f-\tilde f$
belongs to
![]() ${\mathcal {O}}_{mer}(\mathbb C,\Lambda \cup (a+\Lambda ))$
and is invariant both under
${\mathcal {O}}_{mer}(\mathbb C,\Lambda \cup (a+\Lambda ))$
and is invariant both under
![]() $T_1$
and
$T_1$
and
![]() $T_\tau $
, which implies that it belongs to
$T_\tau $
, which implies that it belongs to
![]() $O_{\{pr(0),pr(a)\}}$
, which by Lemma 4.9(b) for
$O_{\{pr(0),pr(a)\}}$
, which by Lemma 4.9(b) for
![]() $S=\{pr(0),pr(a)\}$
is equal to
$S=\{pr(0),pr(a)\}$
is equal to
![]() $O+T_a(O)+\mathbb C(T_a-id)(g_1)$
, and is therefore contained in
$O+T_a(O)+\mathbb C(T_a-id)(g_1)$
, and is therefore contained in
![]() $O[g_1]+T_a(O[g_1])$
. The statement then follows from
$O[g_1]+T_a(O[g_1])$
. The statement then follows from
![]() $\tilde f\in O[g_1]+T_a(O[g_1])$
and
$\tilde f\in O[g_1]+T_a(O[g_1])$
and
![]() $f-\tilde f\in O[g_1]+T_a(O[g_1])$
.
$f-\tilde f\in O[g_1]+T_a(O[g_1])$
.
(b) The proof is by induction on
![]() $n\geq 1$
. For
$n\geq 1$
. For
![]() $n=1$
, the statement follows from (a). Assume the statement at step n and let us prove it at step
$n=1$
, the statement follows from (a). Assume the statement at step n and let us prove it at step
![]() $n+1$
. Let
$n+1$
. Let
![]() $g\in {\mathcal {O}}_{mer}(\mathbb C,\Lambda \cup (a+\Lambda ))$
be such that
$g\in {\mathcal {O}}_{mer}(\mathbb C,\Lambda \cup (a+\Lambda ))$
be such that
![]() $T_1(g)=g$
and
$T_1(g)=g$
and
![]() $(T_\tau -id)^{n+1}(g) \in O[g_1]+T_a(O[g_1])$
. Then
$(T_\tau -id)^{n+1}(g) \in O[g_1]+T_a(O[g_1])$
. Then
![]() $f:=(T_\tau -id)(g)$
is such that
$f:=(T_\tau -id)(g)$
is such that
![]() $T_1(f)=f$
as
$T_1(f)=f$
as
![]() $T_1$
commutes with
$T_1$
commutes with
![]() $T_\tau -id$
, and
$T_\tau -id$
, and
![]() $(T_\tau -id)^n(f) \in O[g_1]+T_a(O[g_1])$
. By the induction assumption, this implies
$(T_\tau -id)^n(f) \in O[g_1]+T_a(O[g_1])$
. By the induction assumption, this implies
![]() $f\in O[g_1]+T_a(O[g_1])$
. Then one has
$f\in O[g_1]+T_a(O[g_1])$
. Then one has
![]() $T_(g)=g$
and
$T_(g)=g$
and
![]() $(T_\tau -id)(g)\in O[g_1]+T_a(O[g_1])$
, which by (a) implies
$(T_\tau -id)(g)\in O[g_1]+T_a(O[g_1])$
, which by (a) implies
![]() $g\in O[g_1]+T_a(O[g_1])$
. This proves the statement at step
$g\in O[g_1]+T_a(O[g_1])$
. This proves the statement at step
![]() $n+1$
.
$n+1$
.
(c) This follows from (b) and from the invariance of
![]() $g_1^n\cdot T_a(g_1)$
under
$g_1^n\cdot T_a(g_1)$
under
![]() $T_1$
, which follows from that of
$T_1$
, which follows from that of
![]() $g_1$
and of
$g_1$
and of
![]() $T_a(g_1)$
, and from
$T_a(g_1)$
, and from
![]() $(T_\tau -id)^{n+2}(g_1^n\cdot T_a(g_1))=0$
.
$(T_\tau -id)^{n+2}(g_1^n\cdot T_a(g_1))=0$
.
Lemma 4.11 One has
![]() $O_S[g_1]=\sum _{s\in S}T_{\tilde s}(O[g_1])$
(equality of subspaces of
$O_S[g_1]=\sum _{s\in S}T_{\tilde s}(O[g_1])$
(equality of subspaces of
![]() ${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
).
${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
).
Proof For
![]() $s\in S$
, one has
$s\in S$
, one has
![]() $T_{\tilde s}(O)\subset O_S\subset O_S[g_1]$
, where the first inclusion follows from Lemma 4.9(b). Moreover,
$T_{\tilde s}(O)\subset O_S\subset O_S[g_1]$
, where the first inclusion follows from Lemma 4.9(b). Moreover,
![]() $T_{\tilde s}(g_1)=g_1+(T_{\tilde s}-id)(g_1)\in O_S[g_1]$
by Lemma 4.9(a). Then
$T_{\tilde s}(g_1)=g_1+(T_{\tilde s}-id)(g_1)\in O_S[g_1]$
by Lemma 4.9(a). Then
![]() $T_{\tilde s}(O[g_1])$
is the subalgebra of
$T_{\tilde s}(O[g_1])$
is the subalgebra of
![]() ${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
generated by
${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
generated by
![]() $T_{\tilde s}(O)$
and
$T_{\tilde s}(O)$
and
![]() $T_{\tilde s}(g_1)$
, which are both contained in
$T_{\tilde s}(g_1)$
, which are both contained in
![]() $O_S[g_1]$
, which implies the inclusion
$O_S[g_1]$
, which implies the inclusion
![]() $T_{\tilde s}(O[g_1])\subset O_S[g_1]$
as
$T_{\tilde s}(O[g_1])\subset O_S[g_1]$
as
![]() $O_S[g_1]$
is an algebra. As
$O_S[g_1]$
is an algebra. As
![]() $O_S[g_1]$
is stable under summation, this implies the inclusion
$O_S[g_1]$
is stable under summation, this implies the inclusion
![]() $O_S[g_1]\supset \sum _{s\in S}T_{\tilde s}(O[g_1])$
.
$O_S[g_1]\supset \sum _{s\in S}T_{\tilde s}(O[g_1])$
.
In order to show the opposite inclusion, let us first show that
![]() $\sum _{s\in S}T_{\tilde s}(O[g_1])$
is a subalgebra of
$\sum _{s\in S}T_{\tilde s}(O[g_1])$
is a subalgebra of
![]() ${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
. For each
${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
. For each
![]() $s\in S$
, the subspace
$s\in S$
, the subspace
![]() $T_{\tilde s}(O[g_1])$
is a subalgebra of
$T_{\tilde s}(O[g_1])$
is a subalgebra of
![]() ${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
. So it is enough to prove that for any
${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
. So it is enough to prove that for any
![]() $s\neq t\in S$
, one has
$s\neq t\in S$
, one has
![]() $T_{\tilde s}(O[g_1])\cdot T_{\tilde t}(O[g_1])\subset T_{\tilde s}(O[g_1])+T_{\tilde t}(O[g_1])$
. By translation invariance, it suffices to prove this for
$T_{\tilde s}(O[g_1])\cdot T_{\tilde t}(O[g_1])\subset T_{\tilde s}(O[g_1])+T_{\tilde t}(O[g_1])$
. By translation invariance, it suffices to prove this for
![]() $t=0$
, in which case
$t=0$
, in which case
![]() $\tilde t=0$
, i.e., to prove
$\tilde t=0$
, i.e., to prove
for
![]() $a\in \mathbb C\smallsetminus \Lambda $
.
$a\in \mathbb C\smallsetminus \Lambda $
.
One has
![]() $O\cdot T_a(O)\subset O_{\{pr(0),pr(a)\}}=O+T_a(O)+\mathbb C\cdot (T_a-id)(g_1)$
where the first inclusion follows from the fact that both O and
$O\cdot T_a(O)\subset O_{\{pr(0),pr(a)\}}=O+T_a(O)+\mathbb C\cdot (T_a-id)(g_1)$
where the first inclusion follows from the fact that both O and
![]() $T_a(O)$
are contained in
$T_a(O)$
are contained in
![]() $O_{\{pr(0),pr(a)\}}$
and that the latter set is an algebra and the second inclusion follows from Lemma 4.9(b) for
$O_{\{pr(0),pr(a)\}}$
and that the latter set is an algebra and the second inclusion follows from Lemma 4.9(b) for
![]() $S=\{pr(0),pr(a)\}$
. This implies
$S=\{pr(0),pr(a)\}$
. This implies
![]() $O\cdot T_a(O)\subset O[g_1]+T_a(O[g_1])$
. Now
$O\cdot T_a(O)\subset O[g_1]+T_a(O[g_1])$
. Now
![]() $O[g_1]\cdot T_a(O[g_1])$
is the sub-
$O[g_1]\cdot T_a(O[g_1])$
is the sub-
![]() $\mathbb C[g_1,T_a(g_1)]$
-module of
$\mathbb C[g_1,T_a(g_1)]$
-module of
![]() ${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
generated by
${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
generated by
![]() $O\cdot T_a(O)$
, therefore in order to prove (4.3.2) it suffices to show that
$O\cdot T_a(O)$
, therefore in order to prove (4.3.2) it suffices to show that
![]() $O[g_1]+T_a(O[g_1])$
is a sub-
$O[g_1]+T_a(O[g_1])$
is a sub-
![]() $\mathbb C[g_1,T_a(g_1)]$
-module of
$\mathbb C[g_1,T_a(g_1)]$
-module of
![]() ${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
, i.e., is stable under multiplication by
${\mathcal {O}}_{mer}(\mathbb C, pr^{-1}(S))$
, i.e., is stable under multiplication by
![]() $g_1$
and
$g_1$
and
![]() $T_a(g_1)$
. The inclusions
$T_a(g_1)$
. The inclusions
![]() $O[g_1]\cdot g_1\subset O[g_1]$
and
$O[g_1]\cdot g_1\subset O[g_1]$
and
![]() $T_a(O[g_1])\cdot T_a(g_1)\subset T_a(O[g_1])$
are obvious, it therefore remains to prove
$T_a(O[g_1])\cdot T_a(g_1)\subset T_a(O[g_1])$
are obvious, it therefore remains to prove
For
![]() $f\in O$
, one has
$f\in O$
, one has
![]() $f\cdot T_a(g_1)=f(a)T_a(g_1)+(f-f(a))(T_a-id)(g_1)+(f-f(a))g_1$
. Then
$f\cdot T_a(g_1)=f(a)T_a(g_1)+(f-f(a))(T_a-id)(g_1)+(f-f(a))g_1$
. Then
![]() $f(a)T_a(g_1)\in \mathbb CT_a(g_1)$
,
$f(a)T_a(g_1)\in \mathbb CT_a(g_1)$
,
![]() $(f-f(a))g_1\in O[g_1]$
and
$(f-f(a))g_1\in O[g_1]$
and
![]() $(f-f(a))(T_a-id)(g_1)\in O$
as
$(f-f(a))(T_a-id)(g_1)\in O$
as
![]() $f-f(a)$
belongs to O and vanishes at a, while
$f-f(a)$
belongs to O and vanishes at a, while
![]() $(T_a-id)(g_1)$
belongs to
$(T_a-id)(g_1)$
belongs to
![]() $O_{\{0,a\}}$
and has only a simple pole at a. It follows that
$O_{\{0,a\}}$
and has only a simple pole at a. It follows that
Then one has
![]() $Og_1^n\cdot T_a(g_1)\subset O[g_1]g_1^n+\mathbb CT_a(g_1)g_1^n\subset O[g_1]+T_a(O[g_1])$
by virtue of (4.3.4) and (4.3.1). This proves the first inclusion in (4.3.3), the second inclusion is a consequence of it (applying
$Og_1^n\cdot T_a(g_1)\subset O[g_1]g_1^n+\mathbb CT_a(g_1)g_1^n\subset O[g_1]+T_a(O[g_1])$
by virtue of (4.3.4) and (4.3.1). This proves the first inclusion in (4.3.3), the second inclusion is a consequence of it (applying
![]() $T_{-a}$
and replacing a by
$T_{-a}$
and replacing a by
![]() $-a$
).
$-a$
).
This ends the proof of the fact that
![]() $\sum _{s\in S}T_{\tilde s}(O[g_1])$
is a subalgebra of
$\sum _{s\in S}T_{\tilde s}(O[g_1])$
is a subalgebra of
![]() ${\mathcal {O}}_{mer}(\mathbb C,pr^{-1}(S))$
.
${\mathcal {O}}_{mer}(\mathbb C,pr^{-1}(S))$
.
One has
![]() $O_S=\sum _{s\in S}T_s(O)+\sum _{s\in S\smallsetminus \{pr(0)\}}(T_{\tilde s}-id)(g_1)\subset \sum _{s\in S}T_{\tilde s}(O[g_1])$
, where the equality follows from Lemma 4.9(b) and the inclusion follows from
$O_S=\sum _{s\in S}T_s(O)+\sum _{s\in S\smallsetminus \{pr(0)\}}(T_{\tilde s}-id)(g_1)\subset \sum _{s\in S}T_{\tilde s}(O[g_1])$
, where the equality follows from Lemma 4.9(b) and the inclusion follows from
![]() $(T_{\tilde s}-id)(g_1)\in O[g_1]+T_{\tilde s}(O[g_1])$
for any
$(T_{\tilde s}-id)(g_1)\in O[g_1]+T_{\tilde s}(O[g_1])$
for any
![]() $s\in S\smallsetminus \{pr(0)\}$
. One also has
$s\in S\smallsetminus \{pr(0)\}$
. One also has
![]() $g_1\in T_0(O[g_1])\subset \sum _{s\in S}T_{\tilde s}(O[g_1])$
. These two statements, together with the fact that
$g_1\in T_0(O[g_1])\subset \sum _{s\in S}T_{\tilde s}(O[g_1])$
. These two statements, together with the fact that
![]() $\sum _{s\in S}T_{\tilde s}(O[g_1])$
is an algebra, implies the inclusion
$\sum _{s\in S}T_{\tilde s}(O[g_1])$
is an algebra, implies the inclusion
![]() $O_S[g_1]\subset \sum _{s\in S}T_{\tilde s}(O[g_1])$
.
$O_S[g_1]\subset \sum _{s\in S}T_{\tilde s}(O[g_1])$
.
Lemma 4.12 The vector subspace
![]() $\sum _{s\in S}T_{\tilde s}(\mathrm {Span}_{\mathbb C}\{g_n\,|\,n\geq 0\})\subset O_S[g_1]$
is such that
$\sum _{s\in S}T_{\tilde s}(\mathrm {Span}_{\mathbb C}\{g_n\,|\,n\geq 0\})\subset O_S[g_1]$
is such that
in other words, the cokernel of the endomorphism
![]() $\partial $
of
$\partial $
of
![]() $O_S[g_1]$
is linearly spanned by the image of the family
$O_S[g_1]$
is linearly spanned by the image of the family
![]() $\{T_{\tilde s}(g_n)\,|\,(s,n)\in S\times \mathbb Z_{\geq 0}\}$
.
$\{T_{\tilde s}(g_n)\,|\,(s,n)\in S\times \mathbb Z_{\geq 0}\}$
.
Proof One has
 $$ \begin{align*} O_S[g_1] &=\sum_{s\in S}T_{\tilde s}(O[g_1]) =\sum_{s\in S}T_{\tilde s}(\partial(O[g_1])+\mathrm{Span}_{\mathbb C}\{g_n\,|\,n\geq 0\}) \\ & =\sum_{s\in S}T_{\tilde s}(\partial(O[g_1]))+\sum_{s\in S}T_{\tilde s}(\mathrm{Span}_{\mathbb C}\{g_n\,|\,n\geq 0\}) \\ &=\partial(\sum_{s\in S}T_{\tilde s}(O[g_1]))+\sum_{s\in S}T_{\tilde s}(\mathrm{Span}_{\mathbb C}\{g_n\,|\,n\geq 0\}) \\ & =\partial(O_S[g_1])+\sum_{s\in S}T_{\tilde s}(\mathrm{Span}_{\mathbb C}\{g_n\,|\,n\geq 0\}), \end{align*} $$
$$ \begin{align*} O_S[g_1] &=\sum_{s\in S}T_{\tilde s}(O[g_1]) =\sum_{s\in S}T_{\tilde s}(\partial(O[g_1])+\mathrm{Span}_{\mathbb C}\{g_n\,|\,n\geq 0\}) \\ & =\sum_{s\in S}T_{\tilde s}(\partial(O[g_1]))+\sum_{s\in S}T_{\tilde s}(\mathrm{Span}_{\mathbb C}\{g_n\,|\,n\geq 0\}) \\ &=\partial(\sum_{s\in S}T_{\tilde s}(O[g_1]))+\sum_{s\in S}T_{\tilde s}(\mathrm{Span}_{\mathbb C}\{g_n\,|\,n\geq 0\}) \\ & =\partial(O_S[g_1])+\sum_{s\in S}T_{\tilde s}(\mathrm{Span}_{\mathbb C}\{g_n\,|\,n\geq 0\}), \end{align*} $$
where the first and last equalities follow from Lemma 4.11, the second equality follows from (4.2.2), the third equality follows from the linearity of
![]() $T_{\tilde s}$
, and the fourth equality follows from the commutativity of
$T_{\tilde s}$
, and the fourth equality follows from the commutativity of
![]() $\partial $
and
$\partial $
and
![]() $T_{\tilde s}$
.
$T_{\tilde s}$
.
Lemma 4.13 The sum map
is a vector space isomorphism.
Proof One has
 $$ \begin{align*} O_S[g_1] &=\sum_{s \in S}T_{\tilde s}(O[g_1]) =\sum_{s\in S}T_{\tilde s}(\mathbb C1+\mathrm{Span}\{g_n|n>0\}+\partial(O[g_1])) \\ & =\mathbb C1+\sum_{s \in S}T_{\tilde s}(\mathrm{Span}\{g_n|n>0\}) +\partial(\sum_{s\in S} T_{\tilde s}(O[g_1])) \\ &=\mathbb C1+\sum_{s \in S}T_{\tilde s}(\mathrm{Span}\{g_n|n>0\})+\partial(O_S[g_1]) \end{align*} $$
$$ \begin{align*} O_S[g_1] &=\sum_{s \in S}T_{\tilde s}(O[g_1]) =\sum_{s\in S}T_{\tilde s}(\mathbb C1+\mathrm{Span}\{g_n|n>0\}+\partial(O[g_1])) \\ & =\mathbb C1+\sum_{s \in S}T_{\tilde s}(\mathrm{Span}\{g_n|n>0\}) +\partial(\sum_{s\in S} T_{\tilde s}(O[g_1])) \\ &=\mathbb C1+\sum_{s \in S}T_{\tilde s}(\mathrm{Span}\{g_n|n>0\})+\partial(O_S[g_1]) \end{align*} $$
where the second equality follows from Lemma 4.8(c), the third equality follows from the commutativity of
![]() $T_{\tilde s}$
with
$T_{\tilde s}$
with
![]() $\partial $
, the fourth equality follows from Lemma 4.11; this implies that the said sum map is surjective.
$\partial $
, the fourth equality follows from Lemma 4.11; this implies that the said sum map is surjective.
Let us prove its injectivity. Let
![]() $P \in O_S[g_1]$
and
$P \in O_S[g_1]$
and
![]() $S \ni s \mapsto t_s \in \mathrm {Span}\{g_n|n>0\}$
and
$S \ni s \mapsto t_s \in \mathrm {Span}\{g_n|n>0\}$
and
![]() $\lambda \in \mathbb C$
be such that
$\lambda \in \mathbb C$
be such that
By Lemma 4.11, there exists a map
![]() $S \ni s \mapsto P_s \in O[g_1]$
such that
$S \ni s \mapsto P_s \in O[g_1]$
such that
![]() $P=\sum _{s \in S}T_{\tilde s}(P_s)$
. Then
$P=\sum _{s \in S}T_{\tilde s}(P_s)$
. Then
(equality in
![]() $O_S[g_1] \subset {\mathcal {O}}_{mer}(\mathbb C,p^{-1}(S))$
).
$O_S[g_1] \subset {\mathcal {O}}_{mer}(\mathbb C,p^{-1}(S))$
).
For each
![]() $s \in \tilde S$
, the equality
$s \in \tilde S$
, the equality
![]() $T_{\tilde s}(\partial (P_s)+t_s)=-\lambda -\sum _{s'\in S\smallsetminus \{s\}}T_{\tilde s'}(\partial (P_s')+t_s')$
implies that the set of poles of
$T_{\tilde s}(\partial (P_s)+t_s)=-\lambda -\sum _{s'\in S\smallsetminus \{s\}}T_{\tilde s'}(\partial (P_s')+t_s')$
implies that the set of poles of
![]() $T_{\tilde s}(\partial (P_s)+t_s)$
is contained in
$T_{\tilde s}(\partial (P_s)+t_s)$
is contained in
![]() $p^{-1}(s) \cap p^{-1}(S\smallsetminus \{s\})$
, which is empty; so
$p^{-1}(s) \cap p^{-1}(S\smallsetminus \{s\})$
, which is empty; so
![]() $T_{\tilde s}(\partial (P_s)+t_s)$
is an element of
$T_{\tilde s}(\partial (P_s)+t_s)$
is an element of
![]() $O[g_1]$
which is holomorphic on
$O[g_1]$
which is holomorphic on
![]() $\mathbb C$
, therefore is constant by Lemma 4.5. Therefore there exists a map
$\mathbb C$
, therefore is constant by Lemma 4.5. Therefore there exists a map
![]() $S \ni s \mapsto \lambda _s \in \mathbb C$
such that
$S \ni s \mapsto \lambda _s \in \mathbb C$
such that
![]() $T_{\tilde s}(\partial (P_s)+t_s)=\lambda _s$
for any
$T_{\tilde s}(\partial (P_s)+t_s)=\lambda _s$
for any
![]() $s \in S$
, and therefore
$s \in S$
, and therefore
Then
![]() $\partial (P_s)=T_{\tilde s}^{-1}(\lambda _s)-t_s=\lambda _s-t_s$
for any
$\partial (P_s)=T_{\tilde s}^{-1}(\lambda _s)-t_s=\lambda _s-t_s$
for any
![]() $s \in S$
. By Lemma 4.8(c), one has for any
$s \in S$
. By Lemma 4.8(c), one has for any
![]() $s \in S$
,
$s \in S$
,
![]() $t_s-\lambda _s=0$
and
$t_s-\lambda _s=0$
and
![]() $\partial (P_s)=0$
. Since
$\partial (P_s)=0$
. Since
![]() $t_s\in \mathrm {Span}\{g_n|n>0\}$
and by Lemma 4.8(b), one derives
$t_s\in \mathrm {Span}\{g_n|n>0\}$
and by Lemma 4.8(b), one derives
![]() $t_s=\lambda _s=0$
. Therefore
$t_s=\lambda _s=0$
. Therefore
![]() $\partial (P)=\sum _s \partial (P_s)=0$
,
$\partial (P)=\sum _s \partial (P_s)=0$
,
![]() $\lambda =\sum _s \lambda _s=0$
, which implies the injectivity.
$\lambda =\sum _s \lambda _s=0$
, which implies the injectivity.
4.4 The equality
 $\mathcal G=A_{{\mathcal {E}}_S}$
$\mathcal G=A_{{\mathcal {E}}_S}$
Lemma 4.14
![]() $\mathcal G$
is equal to the
$\mathcal G$
is equal to the
![]() $O_S[g_1]$
-submodule of
$O_S[g_1]$
-submodule of
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
generated by the functions
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
generated by the functions
![]() $\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
, where
$\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end {smallmatrix};-\right )$
, where
![]() $r\geq 0$
,
$r\geq 0$
,
![]() $n_1,\ldots ,n_r\geq 0$
and
$n_1,\ldots ,n_r\geq 0$
and
![]() $a_1,\ldots ,a_r\in \tilde S$
, namely
$a_1,\ldots ,a_r\in \tilde S$
, namely
 $$ \begin{align*}\mathcal G=\sum_{\substack{r\geq 0,\, n_1,\ldots ,n_r\geq 0,\\ a_1,\ldots ,a_r\in \tilde S}}O_S[g_1]\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end{smallmatrix};-\right). \end{align*} $$
$$ \begin{align*}\mathcal G=\sum_{\substack{r\geq 0,\, n_1,\ldots ,n_r\geq 0,\\ a_1,\ldots ,a_r\in \tilde S}}O_S[g_1]\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_r\\a_1 &a_2 &\ldots &a_r\end{smallmatrix};-\right). \end{align*} $$
Proof This follows from the shuffle identity satisfied by the functions
![]() $\tilde \Gamma $
, which follows from the algebra morphism status of
$\tilde \Gamma $
, which follows from the algebra morphism status of
![]() $k_{\overrightarrow 0}$
.
$k_{\overrightarrow 0}$
.
Set
![]() $\mathrm {int}:=\mathrm {int}_{\omega _0}$
, where
$\mathrm {int}:=\mathrm {int}_{\omega _0}$
, where
![]() $\omega _0:=dz$
. Then
$\omega _0:=dz$
. Then
![]() $\mathrm {int}$
is the endomorphism of
$\mathrm {int}$
is the endomorphism of
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
given by
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
given by
![]() $f\mapsto [z\mapsto \int _{z_0}^z f\omega _0]$
, where
$f\mapsto [z\mapsto \int _{z_0}^z f\omega _0]$
, where
![]() $z_0$
is fixed in
$z_0$
is fixed in
![]() $\tilde {{\mathcal {E}}}_S$
.
$\tilde {{\mathcal {E}}}_S$
.
Definition 4.15 For
![]() $r\geq 0$
, let us set
$r\geq 0$
, let us set
One checks that
![]() $F_\bullet (\mathcal G)$
is an algebra filtration of
$F_\bullet (\mathcal G)$
is an algebra filtration of
![]() $\mathcal G$
.
$\mathcal G$
.
Lemma 4.16 For any
![]() $r,n,n_1,\ldots ,n_r\geq 0$
,
$r,n,n_1,\ldots ,n_r\geq 0$
,
![]() $a_1,\ldots ,a_r\in \tilde S$
and
$a_1,\ldots ,a_r\in \tilde S$
and
![]() $s\in S$
, one has
$s\in S$
, one has
Proof Both
![]() $\mathrm {int}(T_{\tilde s}(g_n)\cdot \tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end {smallmatrix};-\right ))$
and
$\mathrm {int}(T_{\tilde s}(g_n)\cdot \tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end {smallmatrix};-\right ))$
and
![]() $\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r}&n\\a_1 &a_2 & \ldots &a_{r}&\tilde s\end {smallmatrix};-\right )-\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r}&n\\a_1 &a_2 & \ldots &a_{r}&\tilde s\end {smallmatrix};z_0\right )$
are elements of
$\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r}&n\\a_1 &a_2 & \ldots &a_{r}&\tilde s\end {smallmatrix};-\right )-\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r}&n\\a_1 &a_2 & \ldots &a_{r}&\tilde s\end {smallmatrix};z_0\right )$
are elements of
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
. By (3.3.1) their images by
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
. By (3.3.1) their images by
![]() $d : {\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)\to \Omega _{hol}(\tilde {{\mathcal {E}}}_S)$
coincide, and they both vanish at
$d : {\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)\to \Omega _{hol}(\tilde {{\mathcal {E}}}_S)$
coincide, and they both vanish at
![]() $z_0$
. It follows that
$z_0$
. It follows that
This identity implies the statement.
Lemma 4.17 For any
![]() $r,n_1,\ldots ,n_r\geq 0$
and
$r,n_1,\ldots ,n_r\geq 0$
and
![]() $a_1,\ldots ,a_r\in \tilde S$
, one has
$a_1,\ldots ,a_r\in \tilde S$
, one has
Proof By induction on r. For
![]() $r=0$
, and
$r=0$
, and
![]() $f\in O_S[g_1]$
, one has
$f\in O_S[g_1]$
, one has
![]() $\mathrm {int}(\partial (f))=f-f(z_0)\in F_0(\mathcal G)$
. Assume the statement at step
$\mathrm {int}(\partial (f))=f-f(z_0)\in F_0(\mathcal G)$
. Assume the statement at step
![]() $r-1$
. For
$r-1$
. For
![]() $f\in O_S[g_1]$
,
$f\in O_S[g_1]$
,
![]() $n_1,\ldots ,n_r\geq 0$
and
$n_1,\ldots ,n_r\geq 0$
and
![]() $a_1,\ldots ,a_r\in \tilde S$
, integration by parts together with (3.3.1) yields
$a_1,\ldots ,a_r\in \tilde S$
, integration by parts together with (3.3.1) yields
 $$ \begin{align*} \mathrm{int}(\partial(f)\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};-\right)) & =f\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};-\right)-f(z_0)\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};z_0\right) \\ & \quad-\mathrm{int}(f\cdot T_{a_r}(g_{n_r})\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r-1}\\a_1 &a_2 & \ldots &a_{r-1}\end{smallmatrix};-\right)). \end{align*} $$
$$ \begin{align*} \mathrm{int}(\partial(f)\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};-\right)) & =f\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};-\right)-f(z_0)\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};z_0\right) \\ & \quad-\mathrm{int}(f\cdot T_{a_r}(g_{n_r})\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r-1}\\a_1 &a_2 & \ldots &a_{r-1}\end{smallmatrix};-\right)). \end{align*} $$
Note that
![]() $f\cdot \tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end {smallmatrix};-\right )\in F_r(\mathcal G)$
and
$f\cdot \tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end {smallmatrix};-\right )\in F_r(\mathcal G)$
and
![]() $f(z_0)\cdot \tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end {smallmatrix};z_0\right )\in \mathbb C\subset F_0(\mathcal G)$
. Moreover,
$f(z_0)\cdot \tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end {smallmatrix};z_0\right )\in \mathbb C\subset F_0(\mathcal G)$
. Moreover,
![]() $f\in O_S[g_1]$
and
$f\in O_S[g_1]$
and
![]() $T_{a_r}(g_{n_r})\in O_S[g_1]$
by Lemma 4.12, which implies that
$T_{a_r}(g_{n_r})\in O_S[g_1]$
by Lemma 4.12, which implies that
![]() $f\cdot T_{a_r}(g_{n_r})\in O_S[g_1]$
. By Lemma 4.12, one may then decompose
$f\cdot T_{a_r}(g_{n_r})\in O_S[g_1]$
. By Lemma 4.12, one may then decompose
![]() $f\cdot T_{a_r}(g_{n_r})$
as
$f\cdot T_{a_r}(g_{n_r})$
as
![]() $\partial (g)+\sum _{(n,a)\in \mathbb Z_{\geq 0}\times \tilde S} \lambda _{n,a}T_a(g_n)$
, with
$\partial (g)+\sum _{(n,a)\in \mathbb Z_{\geq 0}\times \tilde S} \lambda _{n,a}T_a(g_n)$
, with
![]() $g\in O_S[g_1]$
and
$g\in O_S[g_1]$
and
![]() $\lambda _{n,a}\in \mathbb C$
. Then
$\lambda _{n,a}\in \mathbb C$
. Then
 $$ \begin{align*} &\mathrm{int}(f\cdot T_{a_r}(g_{n_r})\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r-1}\\a_1 &a_2 & \ldots &a_{r-1}\end{smallmatrix};-\right)) \\ & =\mathrm{int}(\partial(g)\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r-1}\\a_1 &a_2 & \ldots &a_{r-1}\end{smallmatrix};-\right))+\sum_{(n,a)\in\mathbb Z_{\geq0}\times\tilde S} \lambda_{n,a} \mathrm{int}(T_a (g_n)\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r-1}\\a_1 &a_2 & \ldots &a_{r-1}\end{smallmatrix};-\right)). \end{align*} $$
$$ \begin{align*} &\mathrm{int}(f\cdot T_{a_r}(g_{n_r})\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r-1}\\a_1 &a_2 & \ldots &a_{r-1}\end{smallmatrix};-\right)) \\ & =\mathrm{int}(\partial(g)\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r-1}\\a_1 &a_2 & \ldots &a_{r-1}\end{smallmatrix};-\right))+\sum_{(n,a)\in\mathbb Z_{\geq0}\times\tilde S} \lambda_{n,a} \mathrm{int}(T_a (g_n)\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r-1}\\a_1 &a_2 & \ldots &a_{r-1}\end{smallmatrix};-\right)). \end{align*} $$
By the induction assumption,
![]() $\mathrm {int}(\partial (g)\cdot \tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r-1}\\a_1 &a_2 & \ldots &a_{r-1}\end {smallmatrix};-\right ))$
belongs to
$\mathrm {int}(\partial (g)\cdot \tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r-1}\\a_1 &a_2 & \ldots &a_{r-1}\end {smallmatrix};-\right ))$
belongs to
![]() $F_{r-1}(\mathcal G)$
. Moreover, for each
$F_{r-1}(\mathcal G)$
. Moreover, for each
![]() $(n,a)$
,
$(n,a)$
,
![]() $ \mathrm {int}(T_a (g_n)\cdot \tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r-1}\\a_1 &a_2 & \ldots &a_{r-1}\end {smallmatrix};-\right ))\in F_r(\mathcal G)$
by Lemma 4.16. All this implies
$ \mathrm {int}(T_a (g_n)\cdot \tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r-1}\\a_1 &a_2 & \ldots &a_{r-1}\end {smallmatrix};-\right ))\in F_r(\mathcal G)$
by Lemma 4.16. All this implies
![]() $\mathrm {int}(\partial (f)\cdot \tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end {smallmatrix};-\right ))\in F_r(\mathcal G)$
, which concludes the inductive argument.
$\mathrm {int}(\partial (f)\cdot \tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end {smallmatrix};-\right ))\in F_r(\mathcal G)$
, which concludes the inductive argument.
Proposition 4.18 For any
![]() $z_0\in \tilde {{\mathcal {E}}}_S$
, the linear endomorphism
$z_0\in \tilde {{\mathcal {E}}}_S$
, the linear endomorphism
![]() $\mathrm {int}$
of
$\mathrm {int}$
of
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
maps
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
maps
![]() $\mathcal G$
to itself.
$\mathcal G$
to itself.
Proof For
![]() $r\geq 0$
, set
$r\geq 0$
, set
 $$ \begin{align*}\mathrm{gr}_r(\mathcal G):= \sum_{\substack{n_1,\ldots ,n_{r}\geq 0,\\ a_1,\ldots ,a_{r}\in \tilde S}} O_S[g_1]\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};-\right). \end{align*} $$
$$ \begin{align*}\mathrm{gr}_r(\mathcal G):= \sum_{\substack{n_1,\ldots ,n_{r}\geq 0,\\ a_1,\ldots ,a_{r}\in \tilde S}} O_S[g_1]\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};-\right). \end{align*} $$
One then has
![]() $F_r(\mathcal G)=\sum _{r'\in [\![0,r]\!]}\mathrm {gr}_{r'}(\mathcal G)$
. We will prove the inclusion
$F_r(\mathcal G)=\sum _{r'\in [\![0,r]\!]}\mathrm {gr}_{r'}(\mathcal G)$
. We will prove the inclusion
![]() $\mathrm {int}(F_r(\mathcal G))\subset F_{r+1}(\mathcal G)$
by induction on
$\mathrm {int}(F_r(\mathcal G))\subset F_{r+1}(\mathcal G)$
by induction on
![]() $r\geq 0$
. Let us first prove that
$r\geq 0$
. Let us first prove that
![]() $\mathrm {int}(F_0(\mathcal G))\subset F_1(\mathcal G)$
.
$\mathrm {int}(F_0(\mathcal G))\subset F_1(\mathcal G)$
.
For
![]() $f\in O_S[g_1]$
, one has
$f\in O_S[g_1]$
, one has
![]() $\mathrm {int}(\partial (f))=f-f(z_0)\in O_S[g_1]$
, which implies that
$\mathrm {int}(\partial (f))=f-f(z_0)\in O_S[g_1]$
, which implies that
It follows from (4.4.1) with
![]() $r=0$
that, for
$r=0$
that, for
![]() $s\in S$
and
$s\in S$
and
![]() $n\geq 0$
, one has
$n\geq 0$
, one has
![]() $\mathrm {int}(T_{\tilde s}(g_n))=\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n\\\tilde s\end {smallmatrix};-\right )-\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n\\\tilde s\end {smallmatrix};z_0\right )$
, which implies that
$\mathrm {int}(T_{\tilde s}(g_n))=\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n\\\tilde s\end {smallmatrix};-\right )-\tilde {\operatorname {\mathrm {\Gamma }}}\left (\begin {smallmatrix}n\\\tilde s\end {smallmatrix};z_0\right )$
, which implies that
Then
 $$ \begin{align*} & \mathrm{int}(F_0(\mathcal G)) =\mathrm{int}(O_S[g_1])=\mathrm{int}(\partial(O_S[g_1])+\sum_{s\in S}T_{\tilde s}(\mathrm{Span}_{\mathbb C}\{g_n\,|\,n\geq0\})) \\ & \quad =\mathrm{int}(\partial(O_S[g_1]))+\sum_{s\in S,n\geq0}\mathbb C\cdot \mathrm{int}(T_{\tilde s}(g_n)) \subset F_0(\mathcal G)+\sum_{s\in S,n\geq0}F_1(\mathcal G)=F_1(\mathcal G), \end{align*} $$
$$ \begin{align*} & \mathrm{int}(F_0(\mathcal G)) =\mathrm{int}(O_S[g_1])=\mathrm{int}(\partial(O_S[g_1])+\sum_{s\in S}T_{\tilde s}(\mathrm{Span}_{\mathbb C}\{g_n\,|\,n\geq0\})) \\ & \quad =\mathrm{int}(\partial(O_S[g_1]))+\sum_{s\in S,n\geq0}\mathbb C\cdot \mathrm{int}(T_{\tilde s}(g_n)) \subset F_0(\mathcal G)+\sum_{s\in S,n\geq0}F_1(\mathcal G)=F_1(\mathcal G), \end{align*} $$
where the first equality follows from
![]() $F_0(\mathcal G)=O_S[g_1]$
, the second equality follows from Lemma 4.12 and the inclusion follows from (4.4.2) and (4.4.3). This proves the initial step of the induction.
$F_0(\mathcal G)=O_S[g_1]$
, the second equality follows from Lemma 4.12 and the inclusion follows from (4.4.2) and (4.4.3). This proves the initial step of the induction.
Assume that
![]() $r\geq 1$
and that
$r\geq 1$
and that
![]() $\mathrm {int}(F_{r-1}(\mathcal G))\subset F_r(\mathcal G)$
. Let us prove that
$\mathrm {int}(F_{r-1}(\mathcal G))\subset F_r(\mathcal G)$
. Let us prove that
![]() $\mathrm {int}(F_r(\mathcal G))\subset F_{r+1}(\mathcal G)$
. One has
$\mathrm {int}(F_r(\mathcal G))\subset F_{r+1}(\mathcal G)$
. One has
![]() $F_{r}(\mathcal G)=F_{r-1}(\mathcal G) +\mathrm {gr}_r(\mathcal G)$
, so by the induction assumption it suffices to prove that
$F_{r}(\mathcal G)=F_{r-1}(\mathcal G) +\mathrm {gr}_r(\mathcal G)$
, so by the induction assumption it suffices to prove that
![]() $\mathrm {int}(\mathrm {gr}_{r}(\mathcal G))\subset F_{r+1}(\mathcal G)$
.
$\mathrm {int}(\mathrm {gr}_{r}(\mathcal G))\subset F_{r+1}(\mathcal G)$
.
Combining Lemma 4.12 with the definition of
![]() $\mathrm {gr}_{r}(\mathcal G)$
, one finds
$\mathrm {gr}_{r}(\mathcal G)$
, one finds
 $$ \begin{align*}\mathrm{gr}_{r}(\mathcal G) &= \sum_{\substack{n_1,\ldots ,n_{r}\geq 0,\\ a_1,\ldots ,a_{r}\in \tilde S}} \partial(O_S[g_1])\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};-\right) \\ &\quad +\sum_{n\geq 0,s\in S}\sum_{\substack{n_1,\ldots ,n_{r}\geq 0,\\ a_1,\ldots ,a_{r}\in \tilde S}} \mathbb C\cdot T_{\tilde s}(g_n)\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};-\right), \end{align*} $$
$$ \begin{align*}\mathrm{gr}_{r}(\mathcal G) &= \sum_{\substack{n_1,\ldots ,n_{r}\geq 0,\\ a_1,\ldots ,a_{r}\in \tilde S}} \partial(O_S[g_1])\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};-\right) \\ &\quad +\sum_{n\geq 0,s\in S}\sum_{\substack{n_1,\ldots ,n_{r}\geq 0,\\ a_1,\ldots ,a_{r}\in \tilde S}} \mathbb C\cdot T_{\tilde s}(g_n)\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};-\right), \end{align*} $$
which implies that
 $$ \begin{align*} \mathrm{int}(\mathrm{gr}_{r}(\mathcal G))&=\sum_{\substack{n_1,\ldots ,n_{r}\geq 0,\\ a_1,\ldots ,a_{r}\in \tilde S}} \mathrm{int}(\partial(O_S[g_1])\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};-\right)) \\ &\quad +\sum_{n\geq 0,s\in S}\sum_{\substack{n_1,\ldots ,n_{r}\geq 0,\\ a_1,\ldots ,a_{r}\in \tilde S}} \mathbb C\cdot \mathrm{int}(T_{\tilde s}(g_n)\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};-\right)), \end{align*} $$
$$ \begin{align*} \mathrm{int}(\mathrm{gr}_{r}(\mathcal G))&=\sum_{\substack{n_1,\ldots ,n_{r}\geq 0,\\ a_1,\ldots ,a_{r}\in \tilde S}} \mathrm{int}(\partial(O_S[g_1])\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};-\right)) \\ &\quad +\sum_{n\geq 0,s\in S}\sum_{\substack{n_1,\ldots ,n_{r}\geq 0,\\ a_1,\ldots ,a_{r}\in \tilde S}} \mathbb C\cdot \mathrm{int}(T_{\tilde s}(g_n)\cdot \tilde{\operatorname{\mathrm{\Gamma}}}\left(\begin{smallmatrix}n_1 &n_2 &\ldots &n_{r}\\a_1 &a_2 & \ldots &a_{r}\end{smallmatrix};-\right)), \end{align*} $$
It follows from Lemma 4.17 (resp. Lemma 4.16) that the first (resp. second) summand of the right-hand side of this equality is contained in
![]() $F_r(\mathcal G)$
(resp.
$F_r(\mathcal G)$
(resp.
![]() $F_{r+1}(\mathcal G)$
), which implies that
$F_{r+1}(\mathcal G)$
), which implies that
![]() $\mathrm {int}(\mathrm {gr}_{r}(\mathcal G))\subset F_{r+1}(\mathcal G)$
.
$\mathrm {int}(\mathrm {gr}_{r}(\mathcal G))\subset F_{r+1}(\mathcal G)$
.
Proposition 4.19 The subspace
![]() $\mathcal G$
of
$\mathcal G$
of
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
is stable under the endomorphism
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
is stable under the endomorphism
![]() $\mathrm {int}_\omega $
for any
$\mathrm {int}_\omega $
for any
![]() $\omega \in \Omega ({\mathcal {E}}_S)$
.
$\omega \in \Omega ({\mathcal {E}}_S)$
.
Proof Since
![]() $\omega _0=dz$
is a nowhere vanishing holomorphic differential, there exists
$\omega _0=dz$
is a nowhere vanishing holomorphic differential, there exists
![]() $f_\omega \in O_S$
such that
$f_\omega \in O_S$
such that
![]() $\omega =f_\omega \cdot \omega _0$
. Then for
$\omega =f_\omega \cdot \omega _0$
. Then for
![]() $f \in \mathcal G$
, one has
$f \in \mathcal G$
, one has
![]() $\mathrm {int}_\omega (f)=\mathrm {int}(f_\omega \cdot f) \in \mathcal G$
, where the equality follows from
$\mathrm {int}_\omega (f)=\mathrm {int}(f_\omega \cdot f) \in \mathcal G$
, where the equality follows from
![]() $\omega =f_\omega \cdot \omega _0$
and the inclusion follows from
$\omega =f_\omega \cdot \omega _0$
and the inclusion follows from
![]() $f_\omega \cdot f \in \mathcal G$
, which stems from the fact that
$f_\omega \cdot f \in \mathcal G$
, which stems from the fact that
![]() $\mathcal G$
is an
$\mathcal G$
is an
![]() $O_S$
-module, and from Proposition 4.18.
$O_S$
-module, and from Proposition 4.18.
Theorem 4.20 One has the equality
![]() $\mathcal G=A_{{\mathcal {E}}_S}$
.
$\mathcal G=A_{{\mathcal {E}}_S}$
.
Proof Proposition 4.19 implies that
![]() $\mathcal G$
is a subalgebra with unit of
$\mathcal G$
is a subalgebra with unit of
![]() ${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
which is stable under the endomorphism
${\mathcal {O}}_{hol}(\tilde {{\mathcal {E}}}_S)$
which is stable under the endomorphism
![]() $\mathrm {int}_\omega $
for any
$\mathrm {int}_\omega $
for any
![]() $\omega \in \Omega ({\mathcal {E}}_S)$
. Together with Lemma-Definition 2.2, this implies that
$\omega \in \Omega ({\mathcal {E}}_S)$
. Together with Lemma-Definition 2.2, this implies that
![]() $\mathcal G \supset A_{{\mathcal {E}}_S}$
. The statement follows from the combination of this inclusion with Corollary 4.4.
$\mathcal G \supset A_{{\mathcal {E}}_S}$
. The statement follows from the combination of this inclusion with Corollary 4.4.
4.5 An
 ${\mathcal {O}}({\mathcal {E}}_S)$
-basis of
${\mathcal {O}}({\mathcal {E}}_S)$
-basis of
 $A_{{\mathcal {E}}_S}$
arising from the functions
$A_{{\mathcal {E}}_S}$
arising from the functions
 $\tilde \Gamma $
$\tilde \Gamma $
Since the ring
![]() $O_S$
is an integral domain, it injects into its fraction field, which is equal to the field
$O_S$
is an integral domain, it injects into its fraction field, which is equal to the field
![]() $\mathbb C({\mathcal {E}})$
of rational functions on
$\mathbb C({\mathcal {E}})$
of rational functions on
![]() ${\mathcal {E}}$
and is therefore independent of S, and will be denoted K. There is a unique extension of the derivation
${\mathcal {E}}$
and is therefore independent of S, and will be denoted K. There is a unique extension of the derivation
![]() $\partial $
of
$\partial $
of
![]() $O_S$
to a derivation of K, which will also be denoted
$O_S$
to a derivation of K, which will also be denoted
![]() $\partial $
.
$\partial $
.
Lemma 4.21 One has
![]() $O_S\cap \partial (K)=\partial (O_S)$
(equality of subspaces of K).
$O_S\cap \partial (K)=\partial (O_S)$
(equality of subspaces of K).
Proof For
![]() $f\in K\smallsetminus \{0\}$
, let
$f\in K\smallsetminus \{0\}$
, let
![]() $\mathrm {Pole}(f) \subset {\mathcal {E}}$
be the set of its poles. If f is nonconstant, then both f and
$\mathrm {Pole}(f) \subset {\mathcal {E}}$
be the set of its poles. If f is nonconstant, then both f and
![]() $\partial (f)$
are in
$\partial (f)$
are in
![]() $K\smallsetminus \{0\}$
, and one has
$K\smallsetminus \{0\}$
, and one has
![]() $\mathrm {Pole}(\partial f)=\mathrm {Pole}(f)$
. On the other hand,
$\mathrm {Pole}(\partial f)=\mathrm {Pole}(f)$
. On the other hand,
![]() $O_S=\{f \in K\smallsetminus \{0\}\,|\,\mathrm {Pole}(f) \subset S\} \cup \{0\}$
. Let now
$O_S=\{f \in K\smallsetminus \{0\}\,|\,\mathrm {Pole}(f) \subset S\} \cup \{0\}$
. Let now
![]() $f\in K$
be such that
$f\in K$
be such that
![]() $\partial (f) \in O_S$
. If
$\partial (f) \in O_S$
. If
![]() $\partial (f)=0$
, then f is constant and so
$\partial (f)=0$
, then f is constant and so
![]() $f \in O_S$
. If
$f \in O_S$
. If
![]() $\partial (f) \neq 0$
, then f is nonzero and
$\partial (f) \neq 0$
, then f is nonzero and
![]() $\mathrm {Pole}(f)=\mathrm {Pole}(\partial f) \subset S$
, therefore
$\mathrm {Pole}(f)=\mathrm {Pole}(\partial f) \subset S$
, therefore
![]() $f \in O_S$
. All this proves the implication
$f \in O_S$
. All this proves the implication
![]() $(f\in K\text { and }\partial (f) \subset O_S)\implies (f\in O_S)$
, which implies the inclusion
$(f\in K\text { and }\partial (f) \subset O_S)\implies (f\in O_S)$
, which implies the inclusion
![]() $O_S \cap \partial (K)\subset \partial (O_S)$
. The opposite inclusion is obvious.
$O_S \cap \partial (K)\subset \partial (O_S)$
. The opposite inclusion is obvious.
Under the isomorphism
![]() $O_S[X]\simeq O_S[g_1]$
, the derivation
$O_S[X]\simeq O_S[g_1]$
, the derivation
![]() $\partial $
of
$\partial $
of
![]() $O_S[g_1]$
is intertwined with the derivation
$O_S[g_1]$
is intertwined with the derivation
![]() $\partial $
of
$\partial $
of
![]() $O_S[X]$
, uniquely defined by the conditions that it extends the derivation
$O_S[X]$
, uniquely defined by the conditions that it extends the derivation
![]() $\partial $
of
$\partial $
of
![]() $O_S$
and that
$O_S$
and that
![]() $\partial (X)=-E_2\subset O\subset O_S$
. This derivation further extends to a derivation
$\partial (X)=-E_2\subset O\subset O_S$
. This derivation further extends to a derivation
![]() $\partial $
of
$\partial $
of
![]() $K[X]$
, extending the derivation
$K[X]$
, extending the derivation
![]() $\partial $
of K.
$\partial $
of K.
Lemma 4.22 The natural map
![]() $O_S[X]/\partial (O_S[X])\to K[X]/\partial (K[X])$
is injective.
$O_S[X]/\partial (O_S[X])\to K[X]/\partial (K[X])$
is injective.
Proof We first prove inductively on
![]() $n \geq 0$
the statement
$n \geq 0$
the statement
Let us prove
![]() $(S_0)$
. Let
$(S_0)$
. Let
![]() $P,Q$
be polynomials satisfying the premise. Then there exist
$P,Q$
be polynomials satisfying the premise. Then there exist
![]() $a_0\in O_S$
and
$a_0\in O_S$
and
![]() $b_0,b_1\in K$
such that
$b_0,b_1\in K$
such that
![]() $P=a_0$
and
$P=a_0$
and
![]() $Q=b_0+b_1X$
. The coefficients of X and of
$Q=b_0+b_1X$
. The coefficients of X and of
![]() $1$
in
$1$
in
![]() $P=\partial (Q)$
respectively yields the equations
$P=\partial (Q)$
respectively yields the equations
The first equation implies
![]() $b_1\in \mathbb C \subset O_S$
. The relation
$b_1\in \mathbb C \subset O_S$
. The relation
![]() $b_1\in \mathbb C$
then implies that the left-hand side of the second equation belongs to
$b_1\in \mathbb C$
then implies that the left-hand side of the second equation belongs to
![]() $O_S$
, while
$O_S$
, while
![]() $b_0\in K$
. By Lemma 4.21, this implies
$b_0\in K$
. By Lemma 4.21, this implies
![]() $b_0\in O_S$
. This proves that
$b_0\in O_S$
. This proves that
![]() $Q \in O_S[X]_{\leq 1}$
, and therefore
$Q \in O_S[X]_{\leq 1}$
, and therefore
![]() $(S_0)$
.
$(S_0)$
.
Assume now
![]() $(S_{n-1})$
to be true for fixed
$(S_{n-1})$
to be true for fixed
![]() $n\geq 1$
, and let us prove
$n\geq 1$
, and let us prove
![]() $(S_n)$
. Let
$(S_n)$
. Let
![]() $P,Q$
be polynomials satisfying the premise. Let
$P,Q$
be polynomials satisfying the premise. Let
![]() $a_0,\ldots ,a_n\in O_S$
and
$a_0,\ldots ,a_n\in O_S$
and
![]() $b_0,\ldots ,b_{n+1}\in K$
be such that
$b_0,\ldots ,b_{n+1}\in K$
be such that
![]() $P=a_0+\cdots +a_nX^n$
and
$P=a_0+\cdots +a_nX^n$
and
![]() $Q=b_0+\cdots +b_{n+1}X^{n+1}$
. The coefficients of
$Q=b_0+\cdots +b_{n+1}X^{n+1}$
. The coefficients of
![]() $X^{n+1}$
and
$X^{n+1}$
and
![]() $X^n$
in
$X^n$
in
![]() $P=\partial (Q)$
respectively yield
$P=\partial (Q)$
respectively yield
The first equation implies
![]() $b_{n+1}\in \mathbb C\subset O_S$
. The relation
$b_{n+1}\in \mathbb C\subset O_S$
. The relation
![]() $b_{n+1}\in \mathbb C$
then implies that the left-hand side of the second equation belongs to
$b_{n+1}\in \mathbb C$
then implies that the left-hand side of the second equation belongs to
![]() $O_S$
, while
$O_S$
, while
![]() $b_n\in K$
. By Lemma 4.21, this implies
$b_n\in K$
. By Lemma 4.21, this implies
![]() $b_n\in O_S$
. Let us set
$b_n\in O_S$
. Let us set
![]() $\tilde Q:=Q-b_{n+1}X^{n+1}-b_nX^n$
and
$\tilde Q:=Q-b_{n+1}X^{n+1}-b_nX^n$
and
![]() $\tilde P:=\partial (\tilde Q)$
. Then
$\tilde P:=\partial (\tilde Q)$
. Then
![]() $\tilde Q\in K[X]_{\leq n-1}$
, which implies
$\tilde Q\in K[X]_{\leq n-1}$
, which implies
![]() $\tilde P\in K[X]_{\leq n-1}$
(because
$\tilde P\in K[X]_{\leq n-1}$
(because
![]() $\tilde P=\partial (\tilde Q)$
and
$\tilde P=\partial (\tilde Q)$
and
![]() $\partial $
maps
$\partial $
maps
![]() $K[X]_{\leq n-1}$
to itself) and
$K[X]_{\leq n-1}$
to itself) and
![]() $\tilde P\in O_S[X]$
(because
$\tilde P\in O_S[X]$
(because
![]() $\tilde P=P-\partial (b_{n+1}X^{n+1}+b_nX^n)$
), and therefore
$\tilde P=P-\partial (b_{n+1}X^{n+1}+b_nX^n)$
), and therefore
![]() $\tilde P\in O_S[X]_{\leq n-1}$
. The relation
$\tilde P\in O_S[X]_{\leq n-1}$
. The relation
![]() $\tilde Q\in K[X]_{\leq n-1}$
also implies
$\tilde Q\in K[X]_{\leq n-1}$
also implies
![]() $\tilde Q\in K[X]_{\leq n}$
. Hence
$\tilde Q\in K[X]_{\leq n}$
. Hence
![]() $(\tilde P,\tilde Q)$
satisfy the assumptions of
$(\tilde P,\tilde Q)$
satisfy the assumptions of
![]() $(S_{n-1})$
. It follows that
$(S_{n-1})$
. It follows that
![]() $\tilde Q\in O_S[X]_{\leq n-1}$
. Since
$\tilde Q\in O_S[X]_{\leq n-1}$
. Since
![]() $b_n,b_{n+1}\in O_S$
, then
$b_n,b_{n+1}\in O_S$
, then
![]() $Q=\tilde Q+b_{n+1}X^{n+1}+b_nX^n\in O_S[X]_{\leq n+1}$
. Therefore
$Q=\tilde Q+b_{n+1}X^{n+1}+b_nX^n\in O_S[X]_{\leq n+1}$
. Therefore
![]() $(P,Q)$
satisfy the conclusion of
$(P,Q)$
satisfy the conclusion of
![]() $(S_n)$
, which proves by induction that
$(S_n)$
, which proves by induction that
![]() $(S_n)$
is true for any
$(S_n)$
is true for any
![]() $n\geq 0$
.
$n\geq 0$
.
Assume now that
![]() $Q\in K[X]$
is such that
$Q\in K[X]$
is such that
![]() $\partial (Q)\in O_S[X]$
. Let
$\partial (Q)\in O_S[X]$
. Let
![]() $n\neq 0$
be such that
$n\neq 0$
be such that
![]() $Q\in K[X]_{\leq n}$
. Then
$Q\in K[X]_{\leq n}$
. Then
![]() $\partial (Q)\in K[X]_{\leq n}$
because
$\partial (Q)\in K[X]_{\leq n}$
because
![]() $\partial $
takes
$\partial $
takes
![]() $K[X]_{\leq n}$
to itself, and since
$K[X]_{\leq n}$
to itself, and since
![]() $\partial (Q)\in O_S[X]$
one has
$\partial (Q)\in O_S[X]$
one has
![]() $\partial (Q)\in O_S[X]_{\leq n}$
. But one also has
$\partial (Q)\in O_S[X]_{\leq n}$
. But one also has
![]() $Q\in K[X]_{\leq n+1}$
, hence
$Q\in K[X]_{\leq n+1}$
, hence
![]() $(P,Q)$
satisfy the assumptions of
$(P,Q)$
satisfy the assumptions of
![]() $(S_n)$
, and therefore
$(S_n)$
, and therefore
![]() $Q\in O_S[X]$
. All this implies the inclusion
$Q\in O_S[X]$
. All this implies the inclusion
![]() $O_S[X]\cap \partial (K[X])\subset \partial (O_S[X])$
. Since the opposite inclusion is obvious, one gets
$O_S[X]\cap \partial (K[X])\subset \partial (O_S[X])$
. Since the opposite inclusion is obvious, one gets
![]() $O_S[X]\cap \partial (K[X])=\partial (O_S[X])$
, which concludes the proof.
$O_S[X]\cap \partial (K[X])=\partial (O_S[X])$
, which concludes the proof.
Lemma 4.23
![]() $O_S[X]$
is an integral domain, and
$O_S[X]$
is an integral domain, and
![]() $O_S[X] \hookrightarrow K(X)$
can be identified with the injection of
$O_S[X] \hookrightarrow K(X)$
can be identified with the injection of
![]() $O_S[X]$
in its fraction field. There is a unique derivation
$O_S[X]$
in its fraction field. There is a unique derivation
![]() $\partial $
of
$\partial $
of
![]() $K(X)$
extending the derivation
$K(X)$
extending the derivation
![]() $\partial $
of
$\partial $
of
![]() $O_S[X]$
.
$O_S[X]$
.
Proof The first statement follows from fact that
![]() $O_S$
is an integral domain. The field
$O_S$
is an integral domain. The field
![]() $K(X)$
contains
$K(X)$
contains
![]() $O_S[X]$
as a subalgebra, and coincides with the smallest of its subfields containing
$O_S[X]$
as a subalgebra, and coincides with the smallest of its subfields containing
![]() $O_S[X]$
, which implies the identification of
$O_S[X]$
, which implies the identification of
![]() $\mathrm {Frac}(O_S[X])$
with
$\mathrm {Frac}(O_S[X])$
with
![]() $K(X)$
. The last statement follows from the fact the a derivation of an integral domain admits a unique extension to its fraction field.
$K(X)$
. The last statement follows from the fact the a derivation of an integral domain admits a unique extension to its fraction field.
Recall the family
![]() $(1,(T_{\tilde s}g_n)_{s\in S,n\geq 1})$
of
$(1,(T_{\tilde s}g_n)_{s\in S,n\geq 1})$
of
![]() $O_S[X]$
(see Lemma 4.12).
$O_S[X]$
(see Lemma 4.12).
Lemma 4.24 The image of the family
![]() $(1,(T_{\tilde s}g_n)_{s\in S,n\geq 1})$
in
$(1,(T_{\tilde s}g_n)_{s\in S,n\geq 1})$
in
![]() $K(X)/\partial (K(X))$
is
$K(X)/\partial (K(X))$
is
![]() $\mathbb C$
-linearly independent.
$\mathbb C$
-linearly independent.
Proof Expansion for X at infinity induces a field extension
![]() $K(X)\subset K((X^{-1}))$
, where
$K(X)\subset K((X^{-1}))$
, where
![]() $K((X^{-1}))$
is the field of Laurent series in the formal variable
$K((X^{-1}))$
is the field of Laurent series in the formal variable
![]() $X^{-1}$
with coefficients in K. On the other hand, there is a double ring inclusion
$X^{-1}$
with coefficients in K. On the other hand, there is a double ring inclusion
![]() $O_S[X]\subset K[X]\subset K(X)$
, thus yielding a sequence of ring inclusions
$O_S[X]\subset K[X]\subset K(X)$
, thus yielding a sequence of ring inclusions
There is a unique derivation
![]() $\partial $
of
$\partial $
of
![]() $K[X]$
, extending
$K[X]$
, extending
![]() $\partial $
on K and such that
$\partial $
on K and such that
![]() $\partial (X)=-E_2$
. Since the derivation
$\partial (X)=-E_2$
. Since the derivation
![]() $\partial $
of
$\partial $
of
![]() $K(X)$
shares these properties, both derivations are compatible. The endomorphism of
$K(X)$
shares these properties, both derivations are compatible. The endomorphism of
![]() $K((X^{-1}))$
given by
$K((X^{-1}))$
given by
![]() $\sum _{i\in \mathbb Z} f_iX^i\mapsto \sum _{i\in \mathbb Z} (\partial (f_i)-E_2(i+1)f_{i+1})X^i$
is well-defined and is a derivation of
$\sum _{i\in \mathbb Z} f_iX^i\mapsto \sum _{i\in \mathbb Z} (\partial (f_i)-E_2(i+1)f_{i+1})X^i$
is well-defined and is a derivation of
![]() $K((X^{-1}))$
. The restriction of this derivation to
$K((X^{-1}))$
. The restriction of this derivation to
![]() $O_S[X]$
coincides with the derivation
$O_S[X]$
coincides with the derivation
![]() $\partial $
of this algebra, therefore its restriction to
$\partial $
of this algebra, therefore its restriction to
![]() $K(X)$
also coincides with the derivation
$K(X)$
also coincides with the derivation
![]() $\partial $
of this field. Hence one obtains a family of compatible derivations on the rings in the sequence of morphisms (4.5.1). From this one derives a sequence of linear maps
$\partial $
of this field. Hence one obtains a family of compatible derivations on the rings in the sequence of morphisms (4.5.1). From this one derives a sequence of linear maps
 $$ \begin{align} O_S[X]/\partial(O_S[X]) &\stackrel{\alpha}{\to} K[X]/\partial(K[X]) \nonumber \\ &\stackrel{\beta}{\to} K(X)/\partial(K(X))\stackrel{\gamma}{\to} K((X^{-1}))/\partial(K((X^{-1}))). \end{align} $$
$$ \begin{align} O_S[X]/\partial(O_S[X]) &\stackrel{\alpha}{\to} K[X]/\partial(K[X]) \nonumber \\ &\stackrel{\beta}{\to} K(X)/\partial(K(X))\stackrel{\gamma}{\to} K((X^{-1}))/\partial(K((X^{-1}))). \end{align} $$
The derivation
![]() $\partial $
of
$\partial $
of
![]() $K((X^{-1}))$
is compatible with the direct sum decomposition
$K((X^{-1}))$
is compatible with the direct sum decomposition
![]() $K((X^{-1}))=K[X] \oplus X^{-1}K[[X^{-1}]]$
, because it is compatible with the derivation
$K((X^{-1}))=K[X] \oplus X^{-1}K[[X^{-1}]]$
, because it is compatible with the derivation
![]() $\partial $
of
$\partial $
of
![]() $K[X]$
and because
$K[X]$
and because
![]() $(\forall i \geq 0, f_i=0)\implies (\forall i \geq 0, \partial (f_i)-(i+1)E_2\,f_{i+1}=0)$
. It follows that the map
$(\forall i \geq 0, f_i=0)\implies (\forall i \geq 0, \partial (f_i)-(i+1)E_2\,f_{i+1}=0)$
. It follows that the map
![]() $\gamma \circ \beta $
is injective, and so that
$\gamma \circ \beta $
is injective, and so that
![]() $\beta $
is injective. By Lemma 4.22, the map
$\beta $
is injective. By Lemma 4.22, the map
![]() $\alpha $
is injective. It follows that
$\alpha $
is injective. It follows that
![]() $\beta \circ \alpha $
is injective, and in particular that it takes
$\beta \circ \alpha $
is injective, and in particular that it takes
![]() $\mathbb C$
-linearly independent families to
$\mathbb C$
-linearly independent families to
![]() $\mathbb C$
-linearly independent families. Then Lemma 4.13, which says that the image of
$\mathbb C$
-linearly independent families. Then Lemma 4.13, which says that the image of
![]() $(1,(T_{\tilde s}g_n)_{s\in S,n\geq 1})$
in
$(1,(T_{\tilde s}g_n)_{s\in S,n\geq 1})$
in
![]() $O_S[X]/\partial (O_S[X])$
is
$O_S[X]/\partial (O_S[X])$
is
![]() $\mathbb C$
-linearly independent, implies the statement.
$\mathbb C$
-linearly independent, implies the statement.
The following statement is a direct consequence of the main result of [Reference Deneufchâtel, Duchamp, Minh, Solomon and WinklerDDMS].
Theorem 4.25 (see [Reference Deneufchâtel, Duchamp, Minh, Solomon and WinklerDDMS], Theorem 1)
Let
![]() $(\mathcal A, \mathbf d)$
be a commutative associative differential algebra with unit over a field
$(\mathcal A, \mathbf d)$
be a commutative associative differential algebra with unit over a field
![]() $\mathbf k$
of characteristic
$\mathbf k$
of characteristic
![]() $0$
, and let
$0$
, and let
![]() $\mathcal C$
be a differential subfield of
$\mathcal C$
be a differential subfield of
![]() $\mathcal A$
(i.e.,
$\mathcal A$
(i.e.,
![]() $\mathbf d(\mathcal C) \subset \mathcal C$
). Let X be a set,
$\mathbf d(\mathcal C) \subset \mathcal C$
). Let X be a set,
![]() $x\mapsto u_x$
be a map
$x\mapsto u_x$
be a map
![]() $X\to \mathcal C$
, and let
$X\to \mathcal C$
, and let
![]() $(r,(x_1,\ldots ,x_r))\mapsto f_{x_1,\ldots ,x_r}$
be a map
$(r,(x_1,\ldots ,x_r))\mapsto f_{x_1,\ldots ,x_r}$
be a map
![]() $\sqcup _{r \geq 0}X^r\to \mathcal A$
, such that
$\sqcup _{r \geq 0}X^r\to \mathcal A$
, such that
![]() $f_\emptyset =1$
and
$f_\emptyset =1$
and
![]() $\mathbf d(f_{x_1,\ldots ,x_r})=u_{x_1}\cdot f_{x_2,\ldots ,x_r}$
for any
$\mathbf d(f_{x_1,\ldots ,x_r})=u_{x_1}\cdot f_{x_2,\ldots ,x_r}$
for any
![]() $r \geq 1$
and
$r \geq 1$
and
![]() $x_1,\ldots ,x_r \in X$
.
$x_1,\ldots ,x_r \in X$
.
If the image of the family
![]() $x\mapsto u_x$
in
$x\mapsto u_x$
in
![]() $\mathcal C/\mathbf d(\mathcal C)$
is
$\mathcal C/\mathbf d(\mathcal C)$
is
![]() $\mathbf k$
-linearly independent, then the family
$\mathbf k$
-linearly independent, then the family
![]() $(r,(x_1,\ldots ,x_r))\mapsto f_{x_1,\ldots ,x_r}$
is
$(r,(x_1,\ldots ,x_r))\mapsto f_{x_1,\ldots ,x_r}$
is
![]() $\mathcal C$
-linearly independent.
$\mathcal C$
-linearly independent.
Proof The hypothesis of the statement is (iii) of Theorem 1 in [Reference Deneufchâtel, Duchamp, Minh, Solomon and WinklerDDMS], and its conclusion is (i) in the same theorem; the statement then follows from Theorem 1 in loc. cit.
Proposition 4.26 (a)
![]() $\mathcal G$
is a free
$\mathcal G$
is a free
![]() $O_S[g_1]$
-module with basis
$O_S[g_1]$
-module with basis
(b)
![]() $\mathcal G$
is a free
$\mathcal G$
is a free
![]() $O_S$
-module with basis
$O_S$
-module with basis
Proof (a) It follows from Lemma 4.14 that (4.5.3) is a generating family of
![]() $\mathcal G$
as an
$\mathcal G$
as an
![]() $O_S[g_1]$
-module.
$O_S[g_1]$
-module.
Recall from Lemma 4.23 that
![]() $O_S[g_1]$
is a integral domain; it therefore fits in an algebra inclusion
$O_S[g_1]$
is a integral domain; it therefore fits in an algebra inclusion
On the other hand, there is an algebra inclusion
where
![]() ${\mathcal {O}}_{mer}(\tilde {{\mathcal {E}}}_S)$
is the algebra of all meromorphic functions on
${\mathcal {O}}_{mer}(\tilde {{\mathcal {E}}}_S)$
is the algebra of all meromorphic functions on
![]() $\tilde {{\mathcal {E}}}_S$
. Moreover, this inclusion is compatible with (4.5.5) and with the module structure of both sides of (4.5.6) over the corresponding algebras of (4.5.5).
$\tilde {{\mathcal {E}}}_S$
. Moreover, this inclusion is compatible with (4.5.5) and with the module structure of both sides of (4.5.6) over the corresponding algebras of (4.5.5).
Let us show that the image of (4.5.3) under (4.5.6) is
![]() $\mathrm {Frac}(O_S[g_1])$
-linearly independent. Set
$\mathrm {Frac}(O_S[g_1])$
-linearly independent. Set
![]() $(\mathcal A,\mathbf d):=({\mathcal {O}}_{mer}(\tilde {{\mathcal {E}}}_S),\partial )$
, set
$(\mathcal A,\mathbf d):=({\mathcal {O}}_{mer}(\tilde {{\mathcal {E}}}_S),\partial )$
, set
![]() $\mathbf k:=\mathbb C$
, set
$\mathbf k:=\mathbb C$
, set
![]() $\mathcal C:=\mathrm {Frac}(O_S[g_1])$
, set
$\mathcal C:=\mathrm {Frac}(O_S[g_1])$
, set
![]() $X:=\{(n,a) \in \mathbb Z_{\geq 0} \times \tilde S\,|\,a=0\text { if }n=0\}$
, let
$X:=\{(n,a) \in \mathbb Z_{\geq 0} \times \tilde S\,|\,a=0\text { if }n=0\}$
, let
![]() $x\mapsto u_x$
be the map
$x\mapsto u_x$
be the map
![]() $X\to \mathcal C$
given by
$X\to \mathcal C$
given by
![]() $(0,0)\mapsto 1$
and
$(0,0)\mapsto 1$
and
![]() $(n,a)\mapsto T_ag_n$
for
$(n,a)\mapsto T_ag_n$
for
![]() $n>0$
, let
$n>0$
, let
![]() $(r,(x_1,\ldots ,x_r))\mapsto f_{x_1,\ldots ,x_r}$
be the map
$(r,(x_1,\ldots ,x_r))\mapsto f_{x_1,\ldots ,x_r}$
be the map
![]() $\sqcup _{r \geq 0}X^r\to \mathcal A$
given by (4.5.3).
$\sqcup _{r \geq 0}X^r\to \mathcal A$
given by (4.5.3).
It follows from (3.3.1) that the identities
![]() $f_\emptyset =1$
and
$f_\emptyset =1$
and
![]() $\mathbf d(f_{x_1,\ldots ,x_r})=u_{x_1}\cdot f_{x_2,\ldots ,x_r}$
are satisfied. It follows from Lemma 4.24 and from the identification
$\mathbf d(f_{x_1,\ldots ,x_r})=u_{x_1}\cdot f_{x_2,\ldots ,x_r}$
are satisfied. It follows from Lemma 4.24 and from the identification
![]() $\mathrm {Frac}(O_S[g_1])\simeq K(X)$
(see Lemma 4.23) that the image of
$\mathrm {Frac}(O_S[g_1])\simeq K(X)$
(see Lemma 4.23) that the image of
![]() $x\mapsto u_x$
in
$x\mapsto u_x$
in
![]() $\mathcal C/\mathbf d(\mathcal C)$
is
$\mathcal C/\mathbf d(\mathcal C)$
is
![]() $\mathbb C$
-linearly independent. We can therefore apply Theorem 4.25, which implies that the image of (4.5.3) under (4.5.6) is
$\mathbb C$
-linearly independent. We can therefore apply Theorem 4.25, which implies that the image of (4.5.3) under (4.5.6) is
![]() $\mathrm {Frac}(O_S[g_1])$
-linearly independent. By the injectivity of the maps (4.5.5) and (4.5.6), this implies the announced statement.
$\mathrm {Frac}(O_S[g_1])$
-linearly independent. By the injectivity of the maps (4.5.5) and (4.5.6), this implies the announced statement.
(b) Let
![]() $\mathcal F:=\sqcup _{r \geq 0} \{(n,a) \in \mathbb Z_{\geq 0} \times \tilde S\,|\,a=0\text { if }n=0\}$
. Let
$\mathcal F:=\sqcup _{r \geq 0} \{(n,a) \in \mathbb Z_{\geq 0} \times \tilde S\,|\,a=0\text { if }n=0\}$
. Let
![]() $\mathbb C^{(\mathcal F)}$
be the set of finitely supported complex functions on
$\mathbb C^{(\mathcal F)}$
be the set of finitely supported complex functions on
![]() $\mathcal F$
. Then (a) says that the map
$\mathcal F$
. Then (a) says that the map
![]() $O_S[g_1] \otimes \mathbb C^{(\mathcal F)}\to \mathcal G$
induced by the family from (a) is a linear isomorphism. Moreover, Lemma 4.6 implies that the map
$O_S[g_1] \otimes \mathbb C^{(\mathcal F)}\to \mathcal G$
induced by the family from (a) is a linear isomorphism. Moreover, Lemma 4.6 implies that the map
![]() $O_S\otimes \mathbb C^{(\mathbb Z_{\geq 0} \times \mathcal F)} \to O_S[g_1] \otimes \mathbb C^{(\mathcal F)}$
given by
$O_S\otimes \mathbb C^{(\mathbb Z_{\geq 0} \times \mathcal F)} \to O_S[g_1] \otimes \mathbb C^{(\mathcal F)}$
given by
![]() $f \otimes \delta _{(i,x)} \mapsto f\cdot g_1^i \otimes \delta _x$
for any
$f \otimes \delta _{(i,x)} \mapsto f\cdot g_1^i \otimes \delta _x$
for any
![]() $x\in \mathcal F$
,
$x\in \mathcal F$
,
![]() $i\in \mathbb Z_{\geq 0}$
,
$i\in \mathbb Z_{\geq 0}$
,
![]() $f\in O_S$
, is a linear isomorphism. Composing these two linear isomorphisms, one obtains that the map
$f\in O_S$
, is a linear isomorphism. Composing these two linear isomorphisms, one obtains that the map
![]() $O_S\otimes \mathbb C^{(\mathbb Z_{\geq 0} \times \mathcal F)} \to \mathcal G$
induced by the family from (b) is a linear isomorphism, which proves (b).
$O_S\otimes \mathbb C^{(\mathbb Z_{\geq 0} \times \mathcal F)} \to \mathcal G$
induced by the family from (b) is a linear isomorphism, which proves (b).
4.6 Examples of relations between elliptic HLs and the functions
 $\tilde \Gamma $
$\tilde \Gamma $
The fact that the iterated integration basepoint for the elliptic HLs
![]() $L_{\alpha _{i_1}\cdots \alpha _{i_n}}$
from Section 2.5 is a fixed point
$L_{\alpha _{i_1}\cdots \alpha _{i_n}}$
from Section 2.5 is a fixed point
![]() $z_0$
different from
$z_0$
different from
![]() $0$
, whereas the iterated integration basepoint for the functions
$0$
, whereas the iterated integration basepoint for the functions
![]() $\tilde \Gamma $
is precisely the point
$\tilde \Gamma $
is precisely the point
![]() $0$
, makes it a bit cumbersome to pass from one basis to the other. We provide below a few examples of expressions which relate elements of the two basis in the simplest setting where
$0$
, makes it a bit cumbersome to pass from one basis to the other. We provide below a few examples of expressions which relate elements of the two basis in the simplest setting where
![]() $S=pr(0)$
consists only of one point. In this case, the basis of differential forms considered in Section 2.5 reduces to
$S=pr(0)$
consists only of one point. In this case, the basis of differential forms considered in Section 2.5 reduces to
![]() $\alpha :=dz$
and
$\alpha :=dz$
and
![]() $\beta :=E_2\,dz$
.
$\beta :=E_2\,dz$
.
Let us introduce the lighter notation
Since
 $\Gamma (\underbrace {0,\ldots ,0}_n;z)={\frac {z^n}{n!}}$
and
$\Gamma (\underbrace {0,\ldots ,0}_n;z)={\frac {z^n}{n!}}$
and
 $L_{\underbrace {\alpha \cdots \alpha }_n}(z)={\frac {(z-z_0)^n}{n!}}$
, one immediately finds the formula
$L_{\underbrace {\alpha \cdots \alpha }_n}(z)={\frac {(z-z_0)^n}{n!}}$
, one immediately finds the formula
 $$ \begin{align*} L_{\underbrace{\alpha\cdots \alpha}_n}\,=\,\sum_{j=0}^n\frac{(-z_0)^{n-j}}{(n-j)!}\tilde{\Gamma}(\underbrace{0,\ldots ,0}_j;-)\,. \end{align*} $$
$$ \begin{align*} L_{\underbrace{\alpha\cdots \alpha}_n}\,=\,\sum_{j=0}^n\frac{(-z_0)^{n-j}}{(n-j)!}\tilde{\Gamma}(\underbrace{0,\ldots ,0}_j;-)\,. \end{align*} $$
Furthermore, since
![]() $E_2=-g^{\prime }_1$
, it follows that
$E_2=-g^{\prime }_1$
, it follows that
Combining this relation with the fact that
![]() $\tilde \Gamma (1;z)=\tilde \Gamma (1;z_0)+\int _{z_0}^zg_1(u)du$
, one gets
$\tilde \Gamma (1;z)=\tilde \Gamma (1;z_0)+\int _{z_0}^zg_1(u)du$
, one gets
Moreover, from (4.6.1) and the shuffle product identity
![]() $L_\beta ^k=k!L_{\scriptsize \underbrace {\beta \cdots \beta }_k}$
, one gets for
$L_\beta ^k=k!L_{\scriptsize \underbrace {\beta \cdots \beta }_k}$
, one gets for
![]() $n\geq 1$
$n\geq 1$
 $$ \begin{align} L_{\underbrace{\beta\cdots \beta}_n}&=\frac{(g_1(z_0)-g_1)^n}{n!},\notag\\ g_1^n&=\sum_{k=0}^n\frac{(-1)^k\,n!}{(n-k)!}\,g_1^{n-k}(z_0)L_{\underbrace{\beta\cdots \beta}_k}. \end{align} $$
$$ \begin{align} L_{\underbrace{\beta\cdots \beta}_n}&=\frac{(g_1(z_0)-g_1)^n}{n!},\notag\\ g_1^n&=\sum_{k=0}^n\frac{(-1)^k\,n!}{(n-k)!}\,g_1^{n-k}(z_0)L_{\underbrace{\beta\cdots \beta}_k}. \end{align} $$
Finally, let us express
![]() $\tilde \Gamma (2;-)$
in terms of elliptic HLs. By Equation (2.4.5), one has
$\tilde \Gamma (2;-)$
in terms of elliptic HLs. By Equation (2.4.5), one has
![]() $g_2=(g_1^2-E_2+e_2)/2$
. Moreover, Equation (4.6.2) for
$g_2=(g_1^2-E_2+e_2)/2$
. Moreover, Equation (4.6.2) for
![]() $n=2$
gives
$n=2$
gives
![]() $g_1^2=2L_{\beta \beta }-2g_1(z_0)L_{\beta }+g_1^2(z_0)$
. Combining these two observations, one gets
$g_1^2=2L_{\beta \beta }-2g_1(z_0)L_{\beta }+g_1^2(z_0)$
. Combining these two observations, one gets
5 Relation of the functions
 $\tilde \Gamma $
with the functions
$\tilde \Gamma $
with the functions
 $\mathrm {E_3}$
$\mathrm {E_3}$
The purpose of this section is to give an alternative proof, based on the results of §4, of the fact that an algebra
![]() $\mathcal A_3$
attached to an elliptic curve
$\mathcal A_3$
attached to an elliptic curve
![]() ${\mathcal {E}}_{alg}$
equipped with a degree 2 ramified covering
${\mathcal {E}}_{alg}$
equipped with a degree 2 ramified covering
![]() ${\mathcal {E}}_{alg}\to \mathbb P^1$
which was constructed in [Reference Broedel, Duhr, Dulat and TancrediBDDT] is stable under integration. In §5.1, we relate the framework of the present paper with the one of [Reference Broedel, Duhr, Dulat and TancrediBDDT]. In Section 5.2, we attach to each finite subset
${\mathcal {E}}_{alg}\to \mathbb P^1$
which was constructed in [Reference Broedel, Duhr, Dulat and TancrediBDDT] is stable under integration. In §5.1, we relate the framework of the present paper with the one of [Reference Broedel, Duhr, Dulat and TancrediBDDT]. In Section 5.2, we attach to each finite subset
![]() $S_0\subset \mathbb P^1_{\mathbb C}$
containing
$S_0\subset \mathbb P^1_{\mathbb C}$
containing
![]() $\infty $
an algebra
$\infty $
an algebra
![]() $\mathcal A_3(S_0)$
, which we prove to be stable under integration using Theorem. 4.20; we derive the fact that the inductive limit of the algebras
$\mathcal A_3(S_0)$
, which we prove to be stable under integration using Theorem. 4.20; we derive the fact that the inductive limit of the algebras
![]() $\mathcal A_3(S_0)$
is stable under integration, and identify this inductive limit with the algebra
$\mathcal A_3(S_0)$
is stable under integration, and identify this inductive limit with the algebra
![]() $\mathcal A_3$
of [Reference Broedel, Duhr, Dulat and TancrediBDDT], thereby giving an alternative proof of the result of this paper (Proposition 5.6(c)).
$\mathcal A_3$
of [Reference Broedel, Duhr, Dulat and TancrediBDDT], thereby giving an alternative proof of the result of this paper (Proposition 5.6(c)).
5.1 Reminders on uniformisation of elliptic curves
Let us denote by
![]() $(z,\tau )\mapsto E_2(z|\tau )$
(resp.
$(z,\tau )\mapsto E_2(z|\tau )$
(resp.
![]() $\tau \mapsto e_2(\tau )$
) the meromorphic (resp. holomorphic) function on
$\tau \mapsto e_2(\tau )$
) the meromorphic (resp. holomorphic) function on
![]() $\mathbb C\times {\mathfrak{H}}$
(resp.
$\mathbb C\times {\mathfrak{H}}$
(resp.
![]() ${\mathfrak{H}}$
) such that for any
${\mathfrak{H}}$
) such that for any
![]() $\tau \in {\mathfrak{H}}$
, the map
$\tau \in {\mathfrak{H}}$
, the map
![]() $z\mapsto E_2(z|\tau )$
(resp. the element
$z\mapsto E_2(z|\tau )$
(resp. the element
![]() $e_2(\tau )\in \mathbb C$
) coincides with the function
$e_2(\tau )\in \mathbb C$
) coincides with the function
![]() $E_2$
(resp. the number
$E_2$
(resp. the number
![]() $e_2\in \mathbb C$
) from §2.4.2. For
$e_2\in \mathbb C$
) from §2.4.2. For
![]() $\tau \in {\mathfrak{H}}$
, we set
$\tau \in {\mathfrak{H}}$
, we set
![]() $\wp (z|\tau ):=E_2(z|\tau )-e_2(\tau )$
.
$\wp (z|\tau ):=E_2(z|\tau )-e_2(\tau )$
.
Denote by
![]() $\mathbb C^3_*$
be the complement of the diagonals in
$\mathbb C^3_*$
be the complement of the diagonals in
![]() $\mathbb C^3$
.
$\mathbb C^3$
.
Lemma 5.1 Let
![]() $(\mathbf a_1,\mathbf a_2,\mathbf a_3)\in \mathbb C^3_*$
. There exists
$(\mathbf a_1,\mathbf a_2,\mathbf a_3)\in \mathbb C^3_*$
. There exists
![]() $\tau \in {\mathfrak{H}}$
,
$\tau \in {\mathfrak{H}}$
,
![]() $a\in \mathbb C^\times $
and
$a\in \mathbb C^\times $
and
![]() $b\in \mathbb C$
such that
$b\in \mathbb C$
such that
Proof The set
![]() $\mathbb C^3_*$
is equipped with the commuting actions of the group
$\mathbb C^3_*$
is equipped with the commuting actions of the group
![]() $\mathbb C^\times \ltimes \mathbb C$
by
$\mathbb C^\times \ltimes \mathbb C$
by
![]() $(a,b)\cdot (\mathbf a_1,\mathbf a_2,\mathbf a_3):=(a\mathbf a_1+b, a\mathbf a_2+b,a\mathbf a_3+b)$
and of the symmetric group
$(a,b)\cdot (\mathbf a_1,\mathbf a_2,\mathbf a_3):=(a\mathbf a_1+b, a\mathbf a_2+b,a\mathbf a_3+b)$
and of the symmetric group
![]() $\mathfrak S_3$
by permutation. The set
$\mathfrak S_3$
by permutation. The set
![]() $\mathbb C\smallsetminus \{0,1\}$
is equipped with an action of
$\mathbb C\smallsetminus \{0,1\}$
is equipped with an action of
![]() $\mathfrak S_3$
, generated by the involutions
$\mathfrak S_3$
, generated by the involutions
![]() $\lambda \mapsto 1-\lambda $
and
$\lambda \mapsto 1-\lambda $
and
![]() $\lambda \mapsto 1/\lambda $
.
$\lambda \mapsto 1/\lambda $
.
The map
![]() $\mathbb C^3_*\to \mathbb C\smallsetminus \{0,1\}$
given by
$\mathbb C^3_*\to \mathbb C\smallsetminus \{0,1\}$
given by
![]() $(\mathbf a_1,\mathbf a_2,\mathbf a_3)\mapsto \mathbf a_{21}/\mathbf a_{31}$
, where we set
$(\mathbf a_1,\mathbf a_2,\mathbf a_3)\mapsto \mathbf a_{21}/\mathbf a_{31}$
, where we set
![]() $\mathbf a_{ij}=\mathbf a_i-\mathbf a_j$
, is
$\mathbf a_{ij}=\mathbf a_i-\mathbf a_j$
, is
![]() $\mathfrak S_3$
-equivariant; it can be identified with the projection
$\mathfrak S_3$
-equivariant; it can be identified with the projection
![]() $\mathbb C^3_*\to (\mathbb C^\times \ltimes \mathbb C)\backslash \mathbb C^3_*$
of
$\mathbb C^3_*\to (\mathbb C^\times \ltimes \mathbb C)\backslash \mathbb C^3_*$
of
![]() $\mathbb C^3_*$
on its set of orbits under the action of
$\mathbb C^3_*$
on its set of orbits under the action of
![]() $\mathbb C^\times \ltimes \mathbb C$
.
$\mathbb C^\times \ltimes \mathbb C$
.
The map
![]() $\mathbb C\smallsetminus \{0,1\}\to \mathbb C$
induced by
$\mathbb C\smallsetminus \{0,1\}\to \mathbb C$
induced by
![]() $\lambda \mapsto 256(1-\lambda +\lambda ^2)^3/(\lambda ^2 (1-\lambda )^2)$
is
$\lambda \mapsto 256(1-\lambda +\lambda ^2)^3/(\lambda ^2 (1-\lambda )^2)$
is
![]() $S_3$
-invariant, and can be identified with the projection
$S_3$
-invariant, and can be identified with the projection
![]() $\mathbb C\smallsetminus \{0,1\}\to \mathfrak S_3\backslash (\mathbb C\smallsetminus \{0,1\})$
of
$\mathbb C\smallsetminus \{0,1\}\to \mathfrak S_3\backslash (\mathbb C\smallsetminus \{0,1\})$
of
![]() $\mathbb C\smallsetminus \{0,1\}$
on the set of its orbits under the action of
$\mathbb C\smallsetminus \{0,1\}$
on the set of its orbits under the action of
![]() $\mathfrak S_3$
.
$\mathfrak S_3$
.
The map
![]() $j : {\mathfrak{H}}\to \mathbb C$
defines a bijection
$j : {\mathfrak{H}}\to \mathbb C$
defines a bijection
![]() $j : \mathrm {SL}_2(\mathbb Z)\backslash {\mathfrak{H}}\to \mathbb C$
. On the other hand, the map
$j : \mathrm {SL}_2(\mathbb Z)\backslash {\mathfrak{H}}\to \mathbb C$
. On the other hand, the map
![]() $\lambda : {\mathfrak{H}}\to \mathbb C\smallsetminus \{0,1\}$
defined by
$\lambda : {\mathfrak{H}}\to \mathbb C\smallsetminus \{0,1\}$
defined by
![]() $\tau \mapsto (\wp (\tau /2|\tau )-\wp (1/2|\tau ))/ (\wp ((1+\tau )/2|\tau )-\wp (1/2|\tau ))$
is compatible with the group morphism
$\tau \mapsto (\wp (\tau /2|\tau )-\wp (1/2|\tau ))/ (\wp ((1+\tau )/2|\tau )-\wp (1/2|\tau ))$
is compatible with the group morphism
![]() $\mathrm {SL}_2(\mathbb Z)\to \mathrm {SL}_2(\mathbb F_2)\simeq \mathfrak S_3$
; it therefore defines a map
$\mathrm {SL}_2(\mathbb Z)\to \mathrm {SL}_2(\mathbb F_2)\simeq \mathfrak S_3$
; it therefore defines a map
![]() $\lambda : \Gamma (2)\backslash {\mathfrak{H}}\to \mathbb C\smallsetminus \{0,1\}$
, which is a bijection. The map
$\lambda : \Gamma (2)\backslash {\mathfrak{H}}\to \mathbb C\smallsetminus \{0,1\}$
, which is a bijection. The map
![]() $\lambda $
is also the composition with the projection
$\lambda $
is also the composition with the projection
![]() $\mathbb C^3_*\to \mathbb C\smallsetminus \{0,1\}$
of the map
$\mathbb C^3_*\to \mathbb C\smallsetminus \{0,1\}$
of the map
![]() ${\mathfrak{H}}\to \mathbb C^3_*$
given by
${\mathfrak{H}}\to \mathbb C^3_*$
given by
![]() $\tau \mapsto (\wp (1/2|\tau ),\wp (\tau /2|\tau ),\wp ((\tau +1)/2|\tau ))$
.
$\tau \mapsto (\wp (1/2|\tau ),\wp (\tau /2|\tau ),\wp ((\tau +1)/2|\tau ))$
.
The situation is summarized in the diagram

where the notation
![]() $X\stackrel {\Gamma }{\to }Y$
means that the map
$X\stackrel {\Gamma }{\to }Y$
means that the map
![]() $X\to Y$
is
$X\to Y$
is
![]() $\Gamma $
-invariant, and sets up a bijection
$\Gamma $
-invariant, and sets up a bijection
![]() $\Gamma \backslash X\stackrel {\sim }{\to } Y$
.
$\Gamma \backslash X\stackrel {\sim }{\to } Y$
.
Let now
![]() $(\mathbf a_1,\mathbf a_2,\mathbf a_3)\in \mathbb C^3_*$
. Its image by the composition
$(\mathbf a_1,\mathbf a_2,\mathbf a_3)\in \mathbb C^3_*$
. Its image by the composition
![]() $\mathbb C^3_*\to \mathbb C\smallsetminus \{0,1\} \to \mathbb C\stackrel {j^{-1}}{\to }\mathrm {SL}_2(\mathbb Z)\backslash {\mathfrak{H}}$
is a well-defined
$\mathbb C^3_*\to \mathbb C\smallsetminus \{0,1\} \to \mathbb C\stackrel {j^{-1}}{\to }\mathrm {SL}_2(\mathbb Z)\backslash {\mathfrak{H}}$
is a well-defined
![]() $\mathrm {SL}_2(\mathbb Z)$
-orbit in
$\mathrm {SL}_2(\mathbb Z)$
-orbit in
![]() ${\mathfrak{H}}$
. Let
${\mathfrak{H}}$
. Let
![]() $\tau _0\in {\mathfrak{H}}$
be an element of this orbit. By the properties of the above diagram, there exists
$\tau _0\in {\mathfrak{H}}$
be an element of this orbit. By the properties of the above diagram, there exists
![]() $\sigma \in \mathfrak S_3$
such that
$\sigma \in \mathfrak S_3$
such that
![]() $\lambda (\tau _0)\in \mathbb C\smallsetminus \{0,1\}$
is related to
$\lambda (\tau _0)\in \mathbb C\smallsetminus \{0,1\}$
is related to
![]() $\mathbf a_{21}/\mathbf a_{31}$
by
$\mathbf a_{21}/\mathbf a_{31}$
by
![]() $\mathbf a_{21}/\mathbf a_{31}=\sigma \cdot \lambda (\tau _0)$
. Let
$\mathbf a_{21}/\mathbf a_{31}=\sigma \cdot \lambda (\tau _0)$
. Let
![]() $\tilde \sigma \in \mathrm {SL}_2(\mathbb Z)$
be a lift of
$\tilde \sigma \in \mathrm {SL}_2(\mathbb Z)$
be a lift of
![]() $\sigma $
, one then has
$\sigma $
, one then has
![]() $\mathbf a_{21}/\mathbf a_{31}=\lambda (\tau )$
, where
$\mathbf a_{21}/\mathbf a_{31}=\lambda (\tau )$
, where
![]() $\tau =\sigma \cdot \tau _0$
. Then the elements
$\tau =\sigma \cdot \tau _0$
. Then the elements
![]() $(\mathbf a_1,\mathbf a_2,\mathbf a_3)$
and
$(\mathbf a_1,\mathbf a_2,\mathbf a_3)$
and
![]() $(\wp (1/2|\tau ),\wp (\tau /2|\tau ),\wp ((\tau +1)/2|\tau ))$
of
$(\wp (1/2|\tau ),\wp (\tau /2|\tau ),\wp ((\tau +1)/2|\tau ))$
of
![]() $\mathbb C^3_*$
have the same image in
$\mathbb C^3_*$
have the same image in
![]() $\mathbb C\smallsetminus \{0,1\}$
, which implies that they are related by the action of
$\mathbb C\smallsetminus \{0,1\}$
, which implies that they are related by the action of
![]() $\mathbb C^\times \ltimes \mathbb C$
.
$\mathbb C^\times \ltimes \mathbb C$
.
In the rest of §5.1, we fix
![]() $\vec {\mathbf a}=(\mathbf a_1,\mathbf a_2,\mathbf a_3)\in \mathbb C^3_*$
.
$\vec {\mathbf a}=(\mathbf a_1,\mathbf a_2,\mathbf a_3)\in \mathbb C^3_*$
.
Definition 5.2
![]() ${\mathcal {E}}_{\mathrm {alg}}$
is the projective curve in
${\mathcal {E}}_{\mathrm {alg}}$
is the projective curve in
![]() $\mathbb P^2(\mathbb C)$
defined by the equation
$\mathbb P^2(\mathbb C)$
defined by the equation
![]() $Y^2T=(X-\mathbf a_1T)(X-\mathbf a_2T)(X-\mathbf a_3T)$
, where
$Y^2T=(X-\mathbf a_1T)(X-\mathbf a_2T)(X-\mathbf a_3T)$
, where
![]() $[X:Y:T]$
is the canonical system of projective coordinates on
$[X:Y:T]$
is the canonical system of projective coordinates on
![]() $\mathbb P^2(\mathbb C)$
.
$\mathbb P^2(\mathbb C)$
.
Lemma 5.3 Let
![]() $(a,b,\tau )\in \mathbb C^\times \times \mathbb C\times {\mathfrak{H}}$
be as in Lemma 5.1, let
$(a,b,\tau )\in \mathbb C^\times \times \mathbb C\times {\mathfrak{H}}$
be as in Lemma 5.1, let
![]() $\Lambda :=\mathbb Z+\mathbb Z\tau $
and
$\Lambda :=\mathbb Z+\mathbb Z\tau $
and
![]() ${\mathcal {E}}:=\mathbb C/\Lambda $
. Let
${\mathcal {E}}:=\mathbb C/\Lambda $
. Let
![]() $a^{3/2}$
be a square root of
$a^{3/2}$
be a square root of
![]() $a^3$
, and denote by
$a^3$
, and denote by
![]() $(z,\tau )\mapsto \wp '(z|\tau )$
the partial derivative of
$(z,\tau )\mapsto \wp '(z|\tau )$
the partial derivative of
![]() $(z,\tau )\mapsto \wp '(z|\tau )$
with respect to z.
$(z,\tau )\mapsto \wp '(z|\tau )$
with respect to z.
(a) There is a unique isomorphism
![]() $iso : {\mathcal {E}}\to {\mathcal {E}}_{\mathrm {alg}}$
, given by
$iso : {\mathcal {E}}\to {\mathcal {E}}_{\mathrm {alg}}$
, given by
![]() $pr(z)\mapsto [a\wp (z|\tau )+b:(1/2)a^{3/2}\wp '(z|\tau ):1]$
for
$pr(z)\mapsto [a\wp (z|\tau )+b:(1/2)a^{3/2}\wp '(z|\tau ):1]$
for
![]() $z\notin \Lambda $
and
$z\notin \Lambda $
and
![]() $pr(0)\mapsto [0:1:0]$
.
$pr(0)\mapsto [0:1:0]$
.
(b) The image by
![]() $iso$
of
$iso$
of
![]() $pr(1/2)$
,
$pr(1/2)$
,
![]() $pr(\tau /2)$
and
$pr(\tau /2)$
and
![]() $pr((1+\tau )/2)$
are respectively
$pr((1+\tau )/2)$
are respectively
![]() ${[\mathbf a_1:0:1]}$
,
${[\mathbf a_1:0:1]}$
,
![]() $[\mathbf a_2:0:1]$
and
$[\mathbf a_2:0:1]$
and
![]() $[\mathbf a_3:0:1]$
. The isomorphism
$[\mathbf a_3:0:1]$
. The isomorphism
![]() $iso$
intertwines the involution
$iso$
intertwines the involution
![]() $pr(z)\mapsto pr(-z)$
of
$pr(z)\mapsto pr(-z)$
of
![]() ${\mathcal {E}}$
with the involution
${\mathcal {E}}$
with the involution
![]() $[X:Y:T]\mapsto [X:-Y:T]$
of
$[X:Y:T]\mapsto [X:-Y:T]$
of
![]() ${\mathcal {E}}_{\mathrm {alg}}$
.
${\mathcal {E}}_{\mathrm {alg}}$
.
Proof (a) follows from the fact that functions
![]() $(z,\tau )\mapsto \wp (z|\tau )$
and
$(z,\tau )\mapsto \wp (z|\tau )$
and
![]() $\wp '(z|\tau )$
satisfy the identity
$\wp '(z|\tau )$
satisfy the identity
![]() $\wp '(z|\tau )^2=4(\wp (z|\tau )-\wp (1/2|\tau ))(\wp (z|\tau )-\wp (\tau /2|\tau ))(\wp (z|\tau )-\wp ((1+\tau )/2|\tau ))$
(see [Reference KnappKn], Theorem 6.15) and from the relation from Lemma 5.1. The first part of (b) follows from Lemma 5.1, from the vanishing for fixed
$\wp '(z|\tau )^2=4(\wp (z|\tau )-\wp (1/2|\tau ))(\wp (z|\tau )-\wp (\tau /2|\tau ))(\wp (z|\tau )-\wp ((1+\tau )/2|\tau ))$
(see [Reference KnappKn], Theorem 6.15) and from the relation from Lemma 5.1. The first part of (b) follows from Lemma 5.1, from the vanishing for fixed
![]() $\tau $
of the function
$\tau $
of the function
![]() $z\mapsto \wp '(z|\tau )$
at
$z\mapsto \wp '(z|\tau )$
at
![]() $1/2$
,
$1/2$
,
![]() $\tau /2$
and
$\tau /2$
and
![]() $(1+\tau )/2$
, which follows from its oddness and from its
$(1+\tau )/2$
, which follows from its oddness and from its
![]() $\Lambda $
-periodicity, and its second part follows from the evenness of the function
$\Lambda $
-periodicity, and its second part follows from the evenness of the function
![]() $z\mapsto \wp (z|\tau )$
and oddness of the function
$z\mapsto \wp (z|\tau )$
and oddness of the function
![]() $z\mapsto \wp '(z|\tau )$
for
$z\mapsto \wp '(z|\tau )$
for
![]() $\tau $
being fixed.
$\tau $
being fixed.
5.2 An alternative proof of a result of [Reference Broedel, Duhr, Dulat and TancrediBDDT]
Let
![]() $\vec {\mathbf a}=(\mathbf a_1,\mathbf a_2,\mathbf a_3)\in \mathbb C^3_*$
, let
$\vec {\mathbf a}=(\mathbf a_1,\mathbf a_2,\mathbf a_3)\in \mathbb C^3_*$
, let
![]() $(a,b,\tau )\in \mathbb C^\times \times \mathbb C\times {\mathfrak{H}}$
be as in Lemma 5.1 and let
$(a,b,\tau )\in \mathbb C^\times \times \mathbb C\times {\mathfrak{H}}$
be as in Lemma 5.1 and let
![]() ${\mathcal {E}},{\mathcal {E}}_{\mathrm {alg}}$
be as in Lemma 5.3 and Definition 5.2.
${\mathcal {E}},{\mathcal {E}}_{\mathrm {alg}}$
be as in Lemma 5.3 and Definition 5.2.
Let
![]() $\pi : {\mathcal {E}}_{\mathrm {alg}}\to \mathbb P^1(\mathbb C)$
be the morphism given by the composition
$\pi : {\mathcal {E}}_{\mathrm {alg}}\to \mathbb P^1(\mathbb C)$
be the morphism given by the composition
![]() ${\mathcal {E}}_{\mathrm {alg}}\subset \mathbb P^2(\mathbb C)\to \mathbb P^1(\mathbb C)$
, where the last morphism is
${\mathcal {E}}_{\mathrm {alg}}\subset \mathbb P^2(\mathbb C)\to \mathbb P^1(\mathbb C)$
, where the last morphism is
![]() $[X:Y:T]\mapsto [X:T]$
. Let
$[X:Y:T]\mapsto [X:T]$
. Let
![]() $S_0 \subset \mathbb P^1(\mathbb C)$
be a finite subset containing
$S_0 \subset \mathbb P^1(\mathbb C)$
be a finite subset containing
![]() $\infty $
. Let
$\infty $
. Let
![]() $S_{\mathrm {alg}}:=\pi ^{-1}(S_0)$
and
$S_{\mathrm {alg}}:=\pi ^{-1}(S_0)$
and
![]() $S:=iso^{-1}(S_{\mathrm {alg}})$
.
$S:=iso^{-1}(S_{\mathrm {alg}})$
.
Then S is a finite subset of
![]() ${\mathcal {E}}$
, which is stable under the involution
${\mathcal {E}}$
, which is stable under the involution
![]() $pr(z)\mapsto pr(-z)$
, and which contains
$pr(z)\mapsto pr(-z)$
, and which contains
![]() $\{pr(0)\}$
; moreover, there is an isomorphism
$\{pr(0)\}$
; moreover, there is an isomorphism
In [Reference Broedel, Duhr, Dulat and TancrediBDDT], (3.16), one defines the family of multivalued holomorphic functions
on
![]() ${\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}$
(denoted
${\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}$
(denoted
![]() $x\mapsto \mathrm {E_3}(\begin {smallmatrix} n_1&\cdots &n_k\\ c_1&\cdots &c_k\end {smallmatrix};x,\vec {\mathbf a})$
in loc. cit. to underscore the dependence in
$x\mapsto \mathrm {E_3}(\begin {smallmatrix} n_1&\cdots &n_k\\ c_1&\cdots &c_k\end {smallmatrix};x,\vec {\mathbf a})$
in loc. cit. to underscore the dependence in
![]() $(\mathbf a_1,\mathbf a_2,\mathbf a_3)$
), indexed by tuples
$(\mathbf a_1,\mathbf a_2,\mathbf a_3)$
), indexed by tuples
![]() $(n_1,c_1),\ldots ,(n_k,c_k)$
in
$(n_1,c_1),\ldots ,(n_k,c_k)$
in
![]() $\sqcup _{k\geq 0}I^k$
, where
$\sqcup _{k\geq 0}I^k$
, where
![]() $I:=(\mathbb Z\times S_0^{unr})\sqcup (\mathbb Z_{\geq 0}\times S_0^{ram})$
and
$I:=(\mathbb Z\times S_0^{unr})\sqcup (\mathbb Z_{\geq 0}\times S_0^{ram})$
and
![]() $S_0^{ram}:=S_0\smallsetminus (S_0\cap \{\mathbf a_1,\mathbf a_2,\mathbf a_3,\infty \})$
and
$S_0^{ram}:=S_0\smallsetminus (S_0\cap \{\mathbf a_1,\mathbf a_2,\mathbf a_3,\infty \})$
and
![]() $S_0^{unr}:=S_0\smallsetminus S_0^{ram}$
; one therefore has for each
$S_0^{unr}:=S_0\smallsetminus S_0^{ram}$
; one therefore has for each
![]() $i\in [\![1,k]\!]$
the relations
$i\in [\![1,k]\!]$
the relations
![]() $(n_i,c_i)\in \mathbb Z\times S_0$
, withFootnote
6
$(n_i,c_i)\in \mathbb Z\times S_0$
, withFootnote
6
![]() $n_i\geq 0$
whenever
$n_i\geq 0$
whenever
![]() $c_i\in \{\mathbf a_1,\mathbf a_2,\mathbf a_3,\infty \}$
.
$c_i\in \{\mathbf a_1,\mathbf a_2,\mathbf a_3,\infty \}$
.
Recall that
![]() $\big (z\mapsto \tilde {\Gamma }(\begin {smallmatrix} n_1&\cdots &n_k\\ a_1&\cdots &a_k\end {smallmatrix};z)\big )$
is a family of multivalued holomorphic functions on
$\big (z\mapsto \tilde {\Gamma }(\begin {smallmatrix} n_1&\cdots &n_k\\ a_1&\cdots &a_k\end {smallmatrix};z)\big )$
is a family of multivalued holomorphic functions on
![]() ${\mathcal {E}}\smallsetminus S$
, indexed by tuples
${\mathcal {E}}\smallsetminus S$
, indexed by tuples
![]() $(n_1,a_1),\ldots ,(n_k,a_k)$
in
$(n_1,a_1),\ldots ,(n_k,a_k)$
in
![]() $\sqcup _{k\geq 0}(\mathbb Z_{\geq 0}\times \tilde S)^k$
.
$\sqcup _{k\geq 0}(\mathbb Z_{\geq 0}\times \tilde S)^k$
.
Proposition 5.4 (see also [Reference Broedel, Duhr, Dulat and TancrediBDDT], Section 5)
The map
![]() $iso^*$
induces an isomorphism of vector spaces between the linear spans
$iso^*$
induces an isomorphism of vector spaces between the linear spans
![]() $\mathrm {Span}_{\mathbb C}\{x\mapsto \mathrm {E_3}(\begin {smallmatrix} n_1&\cdots &n_k\\ c_1&\cdots &c_k\end {smallmatrix};x)\,|\,k\geq 0,(n_i,c_i)\in (\mathbb Z\times S_0^{unr})\sqcup (\mathbb Z_{\geq 0}\times S_0^{ram})\}$
and
$\mathrm {Span}_{\mathbb C}\{x\mapsto \mathrm {E_3}(\begin {smallmatrix} n_1&\cdots &n_k\\ c_1&\cdots &c_k\end {smallmatrix};x)\,|\,k\geq 0,(n_i,c_i)\in (\mathbb Z\times S_0^{unr})\sqcup (\mathbb Z_{\geq 0}\times S_0^{ram})\}$
and
![]() $\mathrm {Span}_{\mathbb C}\{z\mapsto \tilde \Gamma (\begin {smallmatrix} n_1&\cdots &n_k\\ a_1&\cdots &a_k\end {smallmatrix};z)\,|\,k\geq 0,(n_i,a_i)\in \mathbb Z_{\geq 0}\times \tilde S \}$
.
$\mathrm {Span}_{\mathbb C}\{z\mapsto \tilde \Gamma (\begin {smallmatrix} n_1&\cdots &n_k\\ a_1&\cdots &a_k\end {smallmatrix};z)\,|\,k\geq 0,(n_i,a_i)\in \mathbb Z_{\geq 0}\times \tilde S \}$
.
Proof The family of functions
![]() $x\mapsto \mathrm {E_3}(\begin {smallmatrix} n_1&\cdots &n_k\\ c_1&\cdots &c_k\end {smallmatrix};x)$
with variable
$x\mapsto \mathrm {E_3}(\begin {smallmatrix} n_1&\cdots &n_k\\ c_1&\cdots &c_k\end {smallmatrix};x)$
with variable
![]() $(k,(n_1,c_1),\ldots ,(n_k,c_k))$
is defined in [Reference Broedel, Duhr, Dulat and TancrediBDDT] as follows. One introduces in loc. cit. a family of multivalued meromorphic differentials
$(k,(n_1,c_1),\ldots ,(n_k,c_k))$
is defined in [Reference Broedel, Duhr, Dulat and TancrediBDDT] as follows. One introduces in loc. cit. a family of multivalued meromorphic differentials
![]() $\varphi _n(c,t)dt$
on
$\varphi _n(c,t)dt$
on
![]() ${\mathcal {E}}_{\mathrm {alg}}$
, where
${\mathcal {E}}_{\mathrm {alg}}$
, where
![]() $(n,c) \in (\mathbb Z\times S_0^{unr})\sqcup (\mathbb Z_{\geq 0}\times S_0^{ram})$
and
$(n,c) \in (\mathbb Z\times S_0^{unr})\sqcup (\mathbb Z_{\geq 0}\times S_0^{ram})$
and
![]() $S_0^{ram}:=S_0\smallsetminus (S_0\cap \{\mathbf a_1,\mathbf a_2,\mathbf a_3,\infty \})$
with sets of poles contained in
$S_0^{ram}:=S_0\smallsetminus (S_0\cap \{\mathbf a_1,\mathbf a_2,\mathbf a_3,\infty \})$
with sets of poles contained in
![]() $pr_{\mathrm {alg}}^{-1}(S_{\mathrm {alg}})$
, where
$pr_{\mathrm {alg}}^{-1}(S_{\mathrm {alg}})$
, where
![]() $pr_{\mathrm {alg}} : \tilde {{\mathcal {E}}}_{\mathrm {alg}}\to {\mathcal {E}}_{\mathrm {alg}}$
is a universal cover. The functions
$pr_{\mathrm {alg}} : \tilde {{\mathcal {E}}}_{\mathrm {alg}}\to {\mathcal {E}}_{\mathrm {alg}}$
is a universal cover. The functions
![]() $x\mapsto \mathrm {E_3}(\begin {smallmatrix} n_1&\cdots &n_k\\ c_1&\cdots &c_k\end {smallmatrix};x)$
are the iterated integrals of these differentials starting from the point
$x\mapsto \mathrm {E_3}(\begin {smallmatrix} n_1&\cdots &n_k\\ c_1&\cdots &c_k\end {smallmatrix};x)$
are the iterated integrals of these differentials starting from the point
![]() $[0:\sqrt {-\mathbf a_1\mathbf a_2\mathbf a_3}:1]$
in
$[0:\sqrt {-\mathbf a_1\mathbf a_2\mathbf a_3}:1]$
in
![]() ${\mathcal {E}}_{\mathrm {alg}}$
, where
${\mathcal {E}}_{\mathrm {alg}}$
, where
![]() $\sqrt {-\mathbf a_1\mathbf a_2\mathbf a_3}$
is a square root of
$\sqrt {-\mathbf a_1\mathbf a_2\mathbf a_3}$
is a square root of
![]() $-\mathbf a_1\mathbf a_2\mathbf a_3$
. The isomorphism
$-\mathbf a_1\mathbf a_2\mathbf a_3$
. The isomorphism
![]() $iso : {\mathcal {E}}\to {\mathcal {E}}_{\mathrm {alg}}$
induces an isomorphism
$iso : {\mathcal {E}}\to {\mathcal {E}}_{\mathrm {alg}}$
induces an isomorphism
![]() $\widetilde {iso} : \tilde {{\mathcal {E}}}\to \tilde {{\mathcal {E}}}_{\mathrm {alg}}$
, and the image by
$\widetilde {iso} : \tilde {{\mathcal {E}}}\to \tilde {{\mathcal {E}}}_{\mathrm {alg}}$
, and the image by
![]() $\widetilde {iso}^*$
of
$\widetilde {iso}^*$
of
![]() $\mathrm {Span}_{\mathbb C}(\varphi _n(c,t)dt\,|\,(n,c) \in (\mathbb Z\times S_0^{unr})\sqcup (\mathbb Z_{\geq 0}\times S_0^{ram}))$
is a space of multivalued meromorphic differentials on
$\mathrm {Span}_{\mathbb C}(\varphi _n(c,t)dt\,|\,(n,c) \in (\mathbb Z\times S_0^{unr})\sqcup (\mathbb Z_{\geq 0}\times S_0^{ram}))$
is a space of multivalued meromorphic differentials on
![]() ${\mathcal {E}}$
, with sets of poles contained in
${\mathcal {E}}$
, with sets of poles contained in
![]() $pr^{-1}(S)$
, which is shown in [Reference Broedel, Duhr, Dulat and TancrediBDDT], Section 5 to coincide with
$pr^{-1}(S)$
, which is shown in [Reference Broedel, Duhr, Dulat and TancrediBDDT], Section 5 to coincide with
![]() $\mathrm {Span}_{\mathbb C}(dz,T_{a}g_n\cdot dz,a\in pr^{-1}(S))$
. It follows from (2.4.6) that the latter space is equal to
$\mathrm {Span}_{\mathbb C}(dz,T_{a}g_n\cdot dz,a\in pr^{-1}(S))$
. It follows from (2.4.6) that the latter space is equal to
![]() $\mathrm {Span}_{\mathbb C}(dz,T_{a}g_n\cdot dz,a\in \tilde S)$
. So the linear span of the functions
$\mathrm {Span}_{\mathbb C}(dz,T_{a}g_n\cdot dz,a\in \tilde S)$
. So the linear span of the functions
![]() $x\mapsto \mathrm {E_3}(\begin {smallmatrix} n_1&\cdots &n_k\\ c_1&\cdots &c_k\end {smallmatrix};x)$
corresponds via
$x\mapsto \mathrm {E_3}(\begin {smallmatrix} n_1&\cdots &n_k\\ c_1&\cdots &c_k\end {smallmatrix};x)$
corresponds via
![]() $iso^*$
to the linear span of the iterated integrals starting at
$iso^*$
to the linear span of the iterated integrals starting at
![]() $iso(0)$
of the elements of
$iso(0)$
of the elements of
![]() $\mathrm {Span}_{\mathbb C}(dz,T_{a}g_n\cdot dz,a\in \tilde S)$
. By Lemma 3.16(b), this linear span coincides with that of the regularized iterated integrals starting at
$\mathrm {Span}_{\mathbb C}(dz,T_{a}g_n\cdot dz,a\in \tilde S)$
. By Lemma 3.16(b), this linear span coincides with that of the regularized iterated integrals starting at
![]() $pr^{-1}(0)$
of the elements of
$pr^{-1}(0)$
of the elements of
![]() $\mathrm {Span}_{\mathbb C}(dz,T_{a}g_n\cdot dz,a\in \tilde S)$
, which is the linear span of
$\mathrm {Span}_{\mathbb C}(dz,T_{a}g_n\cdot dz,a\in \tilde S)$
, which is the linear span of
![]() $z\mapsto \tilde \Gamma (\begin {smallmatrix} n_1&\cdots &n_k\\ a_1&\cdots &a_k\end {smallmatrix};z)$
for variable
$z\mapsto \tilde \Gamma (\begin {smallmatrix} n_1&\cdots &n_k\\ a_1&\cdots &a_k\end {smallmatrix};z)$
for variable
![]() $(k,(n_1,a_1),\ldots ,(n_k,a_k))$
.
$(k,(n_1,a_1),\ldots ,(n_k,a_k))$
.
The authors of [Reference Broedel, Duhr, Dulat and TancrediBDDT] define in Equation (3.23) a multivalued function
![]() $\mathrm Z_3$
on
$\mathrm Z_3$
on
![]() ${\mathcal {E}}_{\mathrm {alg}}\smallsetminus \{\infty \}$
, closely related to a classical elliptic integral, and prove that
${\mathcal {E}}_{\mathrm {alg}}\smallsetminus \{\infty \}$
, closely related to a classical elliptic integral, and prove that
![]() $iso^*(\mathrm Z_3)=4g_1$
(see [Reference Broedel, Duhr, Dulat and TancrediBDDT], Equation (5.11)).
$iso^*(\mathrm Z_3)=4g_1$
(see [Reference Broedel, Duhr, Dulat and TancrediBDDT], Equation (5.11)).
Proposition 5.5 The subalgebra
of the algebra of holomorphic multivalued functions on
![]() ${\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}$
is stable in the sense of Definition 2.1.
${\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}$
is stable in the sense of Definition 2.1.
Proof Since
![]() $iso^*(\mathrm Z_3)=4g_1$
, it follows that the image by
$iso^*(\mathrm Z_3)=4g_1$
, it follows that the image by
![]() $iso^*$
of this algebra is equal to
$iso^*$
of this algebra is equal to
![]() $\mathcal G$
(see Definition 4.1). The result then follows from Proposition 4.19.
$\mathcal G$
(see Definition 4.1). The result then follows from Proposition 4.19.
Let us emphasize the dependence of
![]() $S_{\mathrm {alg}}$
in the finite subset
$S_{\mathrm {alg}}$
in the finite subset
![]() $S_0$
such that
$S_0$
such that
![]() $\{\infty \}\subset S_0\subset \mathbb P^1_{\mathbb C}$
by denoting it
$\{\infty \}\subset S_0\subset \mathbb P^1_{\mathbb C}$
by denoting it
![]() $S_{\mathrm {alg}}(S_0)$
. Fix: (a) for each finite subset subset
$S_{\mathrm {alg}}(S_0)$
. Fix: (a) for each finite subset subset
![]() $S_0$
such that
$S_0$
such that
![]() $\{\infty \}\subset S_0\subset \mathbb P^1_{\mathbb C}$
, a universal cover
$\{\infty \}\subset S_0\subset \mathbb P^1_{\mathbb C}$
, a universal cover
![]() $\widetilde {{\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S_0)}\to {\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S_0)$
; (b) for each pair of finite sets
$\widetilde {{\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S_0)}\to {\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S_0)$
; (b) for each pair of finite sets
![]() $S_0,S^{\prime }_0$
with
$S_0,S^{\prime }_0$
with
![]() $\{\infty \}\subset S_0\subset S^{\prime }_0\subset \mathbb P^1_{\mathbb C}$
, a holomorphic map
$\{\infty \}\subset S_0\subset S^{\prime }_0\subset \mathbb P^1_{\mathbb C}$
, a holomorphic map
![]() $p_{S_0,S^{\prime }_0} : \widetilde {{\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S^{\prime }_0)} \to \widetilde {{\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S_0)}$
such that
$p_{S_0,S^{\prime }_0} : \widetilde {{\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S^{\prime }_0)} \to \widetilde {{\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S_0)}$
such that

commutes, such that for any triple of finite sets
![]() $S_0,S^{\prime }_0,S^{\prime \prime }_0$
with
$S_0,S^{\prime }_0,S^{\prime \prime }_0$
with
![]() $\{\infty \}\subset S_0\subset S^{\prime }_0\subset S^{\prime \prime }_0\subset \mathbb P^1_{\mathbb C}$
, one has
$\{\infty \}\subset S_0\subset S^{\prime }_0\subset S^{\prime \prime }_0\subset \mathbb P^1_{\mathbb C}$
, one has
![]() $p_{S_0,S^{\prime \prime }_0}=p_{S_0,S^{\prime }_0}\circ p_{S^{\prime }_0,S^{\prime \prime }_0}$
. One can then form the inductive limit algebra
$p_{S_0,S^{\prime \prime }_0}=p_{S_0,S^{\prime }_0}\circ p_{S^{\prime }_0,S^{\prime \prime }_0}$
. One can then form the inductive limit algebra
![]() $\varinjlim _{S_0}{\mathcal {O}}_{hol}(\widetilde {{\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S_0)})$
; it contains the algebra
$\varinjlim _{S_0}{\mathcal {O}}_{hol}(\widetilde {{\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S_0)})$
; it contains the algebra
![]() $\varinjlim _{S_0}{\mathcal {O}}({\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S_0))$
, which is the field
$\varinjlim _{S_0}{\mathcal {O}}({\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S_0))$
, which is the field
![]() $\mathbb C({\mathcal {E}}_{\mathrm {alg}})$
of rational functions on
$\mathbb C({\mathcal {E}}_{\mathrm {alg}})$
of rational functions on
![]() ${\mathcal {E}}_{\mathrm {alg}}$
.
${\mathcal {E}}_{\mathrm {alg}}$
.
Recall that the space of regular differentials on
![]() ${\mathcal {E}}_{\mathrm {alg}}$
is linearly spanned by
${\mathcal {E}}_{\mathrm {alg}}$
is linearly spanned by
![]() $(TdX-XdT)/(YT)$
.
$(TdX-XdT)/(YT)$
.
Proposition 5.6 (a) For each pair of finite sets
![]() $S_0,S^{\prime }_0$
with
$S_0,S^{\prime }_0$
with
![]() $\{\infty \}\subset S_0\subset S^{\prime }_0\subset \mathbb P^1_{\mathbb C}$
, the algebra inclusion
$\{\infty \}\subset S_0\subset S^{\prime }_0\subset \mathbb P^1_{\mathbb C}$
, the algebra inclusion
![]() $p_{S_0,S^{\prime }_0}^* : {\mathcal {O}}_{hol}(\widetilde {{\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S_0)}) \to {\mathcal {O}}_{hol}(\widetilde {{\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S^{\prime }_0)})$
is such that
$p_{S_0,S^{\prime }_0}^* : {\mathcal {O}}_{hol}(\widetilde {{\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S_0)}) \to {\mathcal {O}}_{hol}(\widetilde {{\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S^{\prime }_0)})$
is such that
![]() $p_{S_0,S^{\prime }_0}^* (\mathcal A_3(S_0))\subset \mathcal A_3(S^{\prime }_0)$
. Set
$p_{S_0,S^{\prime }_0}^* (\mathcal A_3(S_0))\subset \mathcal A_3(S^{\prime }_0)$
. Set
![]() $\mathcal A_3:=\varinjlim _{S_0}\mathcal A_3(S_0)$
.
$\mathcal A_3:=\varinjlim _{S_0}\mathcal A_3(S_0)$
.
(b) Let denote the endomorphism
![]() $\mathrm {int}_{(TdX-XdT)/(YT)}$
of
$\mathrm {int}_{(TdX-XdT)/(YT)}$
of
![]() ${\mathcal {O}}_{hol}(\widetilde {{\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S_0)})$
(see §2.1) as
${\mathcal {O}}_{hol}(\widetilde {{\mathcal {E}}_{\mathrm {alg}}\smallsetminus S_{\mathrm {alg}}(S_0)})$
(see §2.1) as
![]() $\mathrm {int}_{S_0}$
. Then for each pair of finite sets
$\mathrm {int}_{S_0}$
. Then for each pair of finite sets
![]() $S_0,S^{\prime }_0$
with
$S_0,S^{\prime }_0$
with
![]() $\{\infty \}\subset S_0\subset S^{\prime }_0\subset \mathbb P^1_{\mathbb C}$
, one has
$\{\infty \}\subset S_0\subset S^{\prime }_0\subset \mathbb P^1_{\mathbb C}$
, one has
![]() $\mathrm {int}_{S_0}\circ p_{S_0,S^{\prime }_0}^*=p_{S_0,S^{\prime }_0}^*\circ \mathrm {int}_{S^{\prime }_0}$
; let
$\mathrm {int}_{S_0}\circ p_{S_0,S^{\prime }_0}^*=p_{S_0,S^{\prime }_0}^*\circ \mathrm {int}_{S^{\prime }_0}$
; let
![]() $\varinjlim _{S_0}\mathrm {int}_{S_0}$
be the corresponding endomorphism of
$\varinjlim _{S_0}\mathrm {int}_{S_0}$
be the corresponding endomorphism of
![]() $\varinjlim _{S_0}{\mathcal {O}}_{hol}(\widetilde {{\mathcal {E}}_{\mathrm {alg}} \smallsetminus S_{\mathrm {alg}}(S_0)})$
.
$\varinjlim _{S_0}{\mathcal {O}}_{hol}(\widetilde {{\mathcal {E}}_{\mathrm {alg}} \smallsetminus S_{\mathrm {alg}}(S_0)})$
.
(c)
![]() $\mathcal A_3$
is stable under
$\mathcal A_3$
is stable under
![]() $\varinjlim _{S_0}\mathrm {int}_{S_0}$
.
$\varinjlim _{S_0}\mathrm {int}_{S_0}$
.
Proof (a) and (b) are straightforward, and (c) follows from Proposition 5.5.
Note that Proposition 5.6(c) recovers the result from [Reference Broedel, Duhr, Dulat and TancrediBDDT], stated in 3 and proved in §6.
Funding
The research of B.E. has been partially funded by ANR grant “Project HighAGT ANR20-CE40-0016”. The research of F.Z. has been funded by the Royal Society, under the grant URF∖R1∖201473.