Eigenfunctions of Operator-Valued Analytic Functions

Extract

This paper is a sequel to [2], whose primary purposes are to clarify and generalize the concept introduced there of an eigenfunction of an inner function, and to answer questions raised there concerning the equivalence of several possible forms of the definition. A new definition, proposed here, leads to a complete characterization of the eigenfunctions of Potapov inner functions of normal operators, and the result is more satisfactory than [2, Theorem 3.4], although the latter is used strongly in the proof.

Let 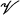be an inner function in the sense of Lax; i.e., 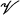is almost everywhere (a.e.) a unitary operator on a separable Hilbert space 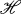and 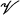belongs weakly to the Hardy class H₂. An analytic function q (which will have to be a scalar inner function) was defined to be an eigenfunction of 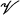if the set of z in the disk {z: |z| ≦ 1} for which is invertible is a set of linear measure 0 on the circle {z: |z| = 1}.