Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-12T08:37:01.361Z Has data issue: false hasContentIssue false
  • English
  • Français

Distinguished Subfields of Intermediate Fields

Published online by Cambridge University Press:  20 November 2018

James K. Deveney  and
John N. Mordeson
James K. Deveney
Affiliation:
Virginia Commonwealth University, Richmond, Virginia
John N. Mordeson
Affiliation:
Virginia Commonwealth University, Richmond, Virginia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let L be a finitely generated extension of a field K of characteristic p ≠ 0. If L/K is algebraic, then there is a unique intermediate field S such that

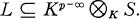
S is just the maximal separable extension of K in L. If L/K is not algebraic, then Dieudonne [4] showed there exist maximal separable extensions D of K in L such that L ⊆ Kp–∞⊗KD. In general, not every maximal separable extension of K in L has the property. Those which do have the property are called distinguished. Kraft [7] established that a maximal separable extension D of K in L is distinguished if and only if [L:D] is as small as possible. If the minimum of the [L:D] is pr, r is called the order of inseparability of L/K, denoted inor (L/K).

Let L1 be an intermediate field of L/K. If L/K is algebraic, then the maximal separable extension S1 of K in L1 is contained in the maximal separable extension S of K in L, and moreover S is separable over S1.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 5 , 01 October 1981 , pp. 1085 - 1096
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Deveney, J. and Mordeson, J., Subfields and invariants of inseparable field extensions, Can. J. Math. 29 (1977), 1304–1311.Google Scholar
2. Deveney, J. and Mordeson, J., The order of inseparability of fields, Can. J. Math. 31 (1979), 655–662.Google Scholar
3. Deveney, J. and Mordeson, J., Distinguished subfields, Trans. Amer. Math. Soc. (to appear).Google Scholar
4. Dieudonne, J., Sur les extensions transcendantes, Summa Brasil. Math. 2 (1947), 1–20.Google Scholar
5. Heerema, N., pth powers of distinguished subfields, Proc. Amer. Math. Soc. 55 (1976), 287–292.Google Scholar
6. Jacobson, N., Lectures in abstract algebra, Vol. III : Theory of fields and Galois theory (Van Nostrand, Princeton, N.J., 1964).Google Scholar
7. Kraft, H., Inseparable Korpererweiterungen, Comment. Math. Helv. 1+5 (1970), 110–118.Google Scholar
8. Kreimer, H. and Heerema, N., Modularity vs. separability for field extensions, Can. J. Math. 27 (1975), 1176–1182.Google Scholar
9. Mordeson, J., Splitting of field extensions, Archiv der Mathematik 26 (1975), 606–610.Google Scholar
10. Mordeson, J. and Vinograde, B., Structure of arbitrary purely inseparable extension fields, Lecture Notes in Math. 173 (Springer-Verlag, Berlin and New York, 1970).Google Scholar