Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-20T14:39:29.171Z Has data issue: false hasContentIssue false
  • English
  • Français

Discrete Curvature and Abelian Groups

Published online by Cambridge University Press:  20 November 2018

Bo'az Klartag ,
Gady Kozma ,
Peter Ralli  and
Prasad Tetali
Bo'az Klartag
Affiliation:
School of Mathematical Sciences, Tel Aviv University, Tel Aviv 69978, Israel e-mail: [email protected]
Gady Kozma
Affiliation:
Department of Mathematics, The Weizmann Institute of Science, Rehovot 76100, Israel e-mail: [email protected]
Peter Ralli
Affiliation:
School of Mathematics and School of Computer Science, Georgia Institute of Technology, Atlanta, GA 30332, USA e-mail: [email protected]@math.gatech.edu
Prasad Tetali
Affiliation:
School of Mathematics and School of Computer Science, Georgia Institute of Technology, Atlanta, GA 30332, USA e-mail: [email protected]@math.gatech.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

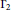We study a natural discrete Bochner-type inequality on graphs, and explore its merit as a notion of “curvature” in discrete spaces. An appealing feature of this discrete version of the so-called ${{\Gamma }_{2}}$-calculus (of Bakry-Émery) seems to be that it is fairly straightforward to compute this notion of curvature parameter for several specific graphs of interest, particularly, abelian groups, slices of the hypercube, and the symmetric group under various sets of generators. We further develop this notion by deriving Buser-type inequalities (à la Ledoux), relating functional and isoperimetric constants associated with a graph. Our derivations provide a tight bound on the Cheeger constant (i.e., the edge-isoperimetric constant) in terms of the spectral gap, for graphs with nonnegative curvature, particularly, the class of abelian Cayley graphs, a result of independent interest.

Keywords

53C2157M15Ricci curvaturegraph theoryabelian groups
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 3 , 01 June 2016 , pp. 655 - 674
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Alon, N., Schwartz, O., and Shapira, A., An elementary construction of constant-degree expanders. Combin. Probab. Comput. 17(2008), no. 3, 319–327. http://dx.doi.org/10.1017/S0963548307008851 Google Scholar
[2] Bakry, D. andÉmery, M., Diéusions hypercontractives. In: Séminaire de probabilités, XIX1983/84, Lecture Notes in Math.,1123, Springer, Berlin, 1985, pp. 177–206. http://dx.doi.org/10.1007/BFb0075847 Google Scholar
[3] Bakry, D., Gentil, I., and Ledoux, M., Analysis and geometry of Markov diffusion operators. Grundlehren der Mathematischen Wissenschaten, 348, Springer, 2014.http://dx.doi.org/10.1007/978-3-319-00227-9 Google Scholar
[4]Barlow, M., Which values of the volume growth and escape time exponent are possible for a graph? Rev. Mat. Iberoamericana 20(2004), no. 1,1-31.http://dx.doi.org/10.4171/RMI/378 Google Scholar
[5] Barlow, M. and Bass, R.,Stability of parabolic Harnack inequalities. Trans. Amer. Math. Soc. 356(2004), no.1501–1533. http://dx.doi.org/10.1090/S0002-9947-03-03414-7 Google Scholar
[6] Bauer, F., Horn, P., Lin, Y., Lippner, G., Mangoubi, D., and Yau, S.-T.,Li-Yau inequality on graphs. J.Differential Geom. 99(2015), no.3,359–405. Google Scholar
[7] I. Benjamini and D. Ellis, On the structure of graphs which are locally indistinguishable from a lattice. arxiv:1409.7587 Google Scholar
[8] Buser, P., A note on the isoperimetric constant. Annales scientifiques de l' École Normale Supérieure 15 (1982), no. 2, 213–230. Google Scholar
[9] Cheeger, J. and Ebin, D., Comparison theorems in Riemannian geometry. North-Holl and Mathematical Library , North-Holland Publishing Co., Amsterdam-Oxford; American Elsevier Publishing Co., Inc., New York, 1975.Google Scholar
[10]Chung, F.. Fourth International Congress of Cheeger inequality and graph partition algorithms. Mathematicians, AMS/IP Stud. Adv. Math. 48 American Mathematical Society, Providence, RI, 2010, pp. 331–349 Google Scholar
[11] Chung, F., Lin, Y., and Yau, S.-T., Harnack inequalities for graphs with non-negative Ricci curvature. J. Math. Anal. Appl. 415(2014), no. 1,25–32. http://dx.doi.org/10.1016/j.jmaa.2014.01.044 Google Scholar
[12] Chung, F. R. K.and Yau, S.-T., Logarithmic Harnack inequalities. Math. Res. Lett. 3(1996), no. 6,793–812.http://dx.doi.org/10.4310/MRL.1996.v3.n6.a8 Google Scholar
[13] Delmotte, T., Graphs between the elliptic and parabolic Harnack inequalities. Potential Anal. 16(2002), no. 2,151–168. http://dx.doi.org/10.1023/A:1012632229879 Google Scholar
[14] Diaconis, P. and Saloff-Coste, L., Logarithmic Sobolev inequalities for finite Markov chains. Ann. Appl. Probab. 6(1996), no. 3, 695–750. http://dx.doi.org/10.1214/aoap/1034968224 Google Scholar
[15] Diaconis, P. , Random walks on ûnite groups: a survey of analytic techniques. In: Probability measures on groups and related structures XI (Oberwolfach,1994 ,pp.44–75.Google Scholar
[16] Erbar, M. and Maas, J., Ricci curvature of ûnite Markov chains via convexity of the entropy. Arch. Ration. Mech. Anal. 206(2012), no.3,997–1038. http://dx.doi.org/10.1007/s00205-012-0554-z Google Scholar
[17] Erbar, M., Maas, J., and Tetali, P., Discrete Ricci curvature bounds for Bernoulli–Laplace and random transposition models. Annales Fac. Sci. Toulouse, to appear. arxiv:1409.8605 Google Scholar
[18] H. Garland, , p-adic curvature and the cohomology of discrete subgroups of p-adic groups. Ann. of Math. (2)97 (1937),375–423.http://dx.doi.org/10.2307/1970829 Google Scholar
[19] Gozlan, N., Roberto, C., Samson, P.-M., and Tetali, P., Displacement convexity of entropy and related inequalities on graphs. Probability Theory and Related Fields 160(2014),47–94. http://dx.doi.org/10.1007/s00440-013-0523-y Google Scholar
[20] Gross, L., Logarithmic Sobolev inequalities. Amer. J. Math. 97(1975), no.4,1061–1083.http://dx.doi.org/10.2307/2373688 Google Scholar
[21] Horn, P. , Lin, Y., Liu, S., and Yau, S.-T. , Volume doubling, Poincaréinequality and Gaussian heat kernel estimate for nonnegative curvature graphs. arxiv:1411.5087Google Scholar
[22] Kozma, G., A graph counterexample to Davies' conjecture. Rev. Mat. Iberoam. 30(2014), no. 1, 1–12. http://dx.doi.org/10.4171/RMI/766 Google Scholar
[23] Ledoux, M., Spectral gap, logarithmic Sobolev constant, and geometric bounds. Surveys in Diff.Geom. 9(2004), 219–240.Google Scholar
[24] Liu, S., and Peyerimhoff, N., Eigenvalue ratios of nonnegatively curved graphs. arxiv:1406.6617Google Scholar
[25] Levin, D., Peres, Y., and Wilmer, E., E., Markov chains and mixing times. American Mathematical Society, Providence RI, 2009.Google Scholar
[26] Lott, J. and Villani, C., Ricci curvature for metric-measure spaces via optimal transport. Ann. Math. (2) 169(2009), no. 3,903–991.http://dx.doi.org/10.4007/annals.2009.169.903 Google Scholar
[27] Lin, Y. and Yau, S.-T., Ricci curvature and eigenvalue estimate on locally ûnite graphs. Math. Res. Lett. 17(2012), no. 2, 343–356. http://dx.doi.org/10.4310/MRL.2010.v17.n2.a13 Google Scholar
[28] R. Montenegro, and P. Tetali, , Mathematical aspects of mixing times in Markov chains. Found. Trends Theoret. Comput. Sci. 1(2006), no. 3.Google Scholar
[29] Münch, F., Remarks on curvature dimension conditions on graphs. arxiv:1501.05839Google Scholar
[30] Ollivier, Y., Ricci curvature of Markov chains on metric spaces. J. Funct. Anal. 256(2009), no. 3, 810–864. http://dx.doi.org/10.1016/j.jfa.2008.11.001 Google Scholar
[31] Papasoglu, P., An algorithm detecting hyperbolicity. In :Geometric and computational perspectives on infinite groups (Minneapolis, MN and New Brunswick, NJ, 1994 ), DIMACS Ser. Discrete Math.Theoret. Comput. Sci., zþ, American Mathematical Society, Providence, RI, 1996, pp.193–200.Google Scholar
[32] Schmuckenschläger, M., Curvature of nonlocal Markov generators. In: Convex geometric analysis (Berkeley, CA, 1996), Cambridge Univ. Press, Cambridge 1999, pp.189–197.Google Scholar
[33] Sammer, M. D., Aspects of mass transportation in discrete concentration inequalities. PhD thesis, Georgia Institute of Technology, 2005. http: //etd.gatech.edu/theses/available/etd-04112005-163457/unrestricted/sammer_marcus_d_200505_phd.pdf Google Scholar
[34] Sturm, K.-Th., On the geometry of metric measure spaces. I. Acta Math. 196(2006), no. 1, 65–131. http://dx.doi.org/10.1007/s11511-006-0002-8 Google Scholar