Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T04:01:11.041Z Has data issue: false hasContentIssue false
  • English
  • Français

Diamond Principles, Ideals and the Normal Moore Space Problem

Published online by Cambridge University Press:  20 November 2018

Alan D. Taylor
Alan D. Taylor*
Affiliation:
Union College, Schenectady, New York
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

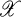If is a topological space then a sequence (Cα:α < λ) of subsets of 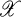is said to be normalized if for every H ⊆ λ there exist disjoint open sets 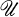and 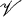such that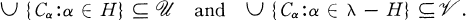

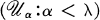The sequence (Cα:α < λ) is said to be separated if there exists a sequence of pairwise disjoint open sets such that 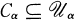for each α < λ. As is customary, we adopt the convention that all sequences (Cα:α < λ) considered are assumed to be relatively discrete as defined in [18, p. 21]: if x ∈ Cα then there exists a neighborhood about x that intersects no Cβ for β ≠ α.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 2 , 01 April 1981 , pp. 282 - 296
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Baumgartner, J., Results and independence proofs in combinatorial set theory, thesis, University of California at Berkeley (1970).Google Scholar
2. Baumgartner, J., Taylor, A. and Wagon, S., Structural properties of ideals, to appear in Dissertationes Mathematicae.Google Scholar
3. Bing, R. H., Metrization of topological spaces, Can. J. Math. 3 (1951), 175–186.Google Scholar
4. Charlesworth, A., Hodel, R. and Tall, F., On a theorem of Jones and Heath concerning discrete subspaces, Colloq. Math. 34 (1975), 33–37.Google Scholar
5. Devlin, K., Aspects of constructibility, Lecture notes in Mathematics 354 (Springer-Verlag, Berlin-Heidelberg-New York, 1973).Google Scholar
6. Devlin, K. and Shelah, S., A weak version of • which follows from 2^° < 2*1, Israel Journal of Math. 29 (1978), 239–247.Google Scholar
7. Devlin, K. and Shelah, S., A note on the normal Moore space conjecture, Can. J. Math. 31 (1979), 241–251.Google Scholar
8. Devlin, K. and Shelah, S., Souslin properties and tree topologies, Proc. of the London Math. Soc. (to appear).Google Scholar
9. Fleissner, W., Normal Moore spaces in the constructible universe, Proc. Amer. Math. Soc. 46 (1974), 294–298.Google Scholar
10. Fleissner, W., When is Jones’ space normal? Proc. Amer. Math. Soc. 50 (1975), 375–378.Google Scholar
11. Fleissner, W., Current research on Q-sets, Proc. Bolyai Janos Society Colloquium on Topology (Budapest, 1978), to appear.Google Scholar
12. Heath, R., Screenability, pointwise paracompactness and metrization of Moore spaces, Can. J. Math. 16 (1964), 763–770.Google Scholar
13. Jensen, R. and Kunen, K., Some combinatorial properties of L and V, mimeograph.Google Scholar
14. Jones, F. B., Concerning normal and completely normal spaces, Bull. Amer. Math. Soc. 43 (1937), 671–677.Google Scholar
15. Nyikos, P., A provisional solution to the normal Moore space problem, Proc. Amer. Math. Soc. (to appear).Google Scholar
16. Rudin, M. E., Lectures on set theoretic topology, Regional Conf. Ser. 23 (Amer. Math. Soc, Providence, 1975).Google Scholar
17. Sapirovskii, B., On separability and metrizability of spaces with Souslin s condition, Soviet Math. Dokl. 13 (1972), 1633–1638.Google Scholar
18. Tall, F., Set-theoretic consistency results and topological theorems concerning the normal Moore space conjecture and related problems, Dissertationes Mathematicae 148 (1977).Google Scholar
19. Tall, F., Weakly collectionwise Hausdorff spaces, Topology Proceedings 1 (1976), 295–304.Google Scholar
20. Tall, F., The normal Moore space problem, topological structures II, Math. Res. Centre (Amsterdam), to appear.Google Scholar