Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T06:29:08.855Z Has data issue: false hasContentIssue false
  • English
  • Français

Diametrically Maximal and Constant Width Sets in Banach Spaces

Published online by Cambridge University Press:  20 November 2018

J. P. Moreno ,
P. L. Papini  and
R. R. Phelps
J. P. Moreno
Affiliation:
Dpto. Matemáticas, Facultad de Ciencias, Universidad Autónoma de Madrid, Madrid 28049, Spain e-mail: [email protected]
P. L. Papini
Affiliation:
Dipartimento di Matematica, Piazza Porta S. Donato 5, 40126 Bologna, Italy e-mail: [email protected]
R. R. Phelps
Affiliation:
Department of Mathematics, Box 354-350, University of Washington, Seattle, WA 98195, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

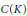We characterize diametrically maximal and constant width sets in $C(K)$, where 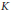$K$ is any compact Hausdorff space. These results are applied to prove that the sum of two diametrically maximal sets needs not be diametrically maximal, thus solving a question raised in a paper by Groemer. A characterization of diametrically maximal sets in 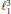$\ell _{1}^{3}$ is also given, providing a negative answer to Groemer's problem in finite dimensional spaces. We characterize constant width sets in 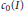${{c}_{0}}\left( I \right)$, for every 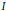$I$, and then we establish the connections between the Jung constant of a Banach space and the existence of constant width sets with empty interior. Porosity properties of families of sets of constant width and rotundity properties of diametrically maximal sets are also investigated. Finally, we present some results concerning non-reflexive and Hilbert spaces.

Keywords

52A0546B20
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 4 , 01 August 2006 , pp. 820 - 842
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Amir, D., On Jung's constant and related constants in normed linear spaces. Pacific J. Math. 118(1985), No. 1, 1–15.Google Scholar
[2] Behrends, E., Points of symmetry of convex sets in the two-dimensional complex space—a counterexample to D. Yost's problem. Math. Ann. 290(1991), no. 3, 463–471.Google Scholar
[3] Behrends, E., and Harmand, P., Banach spaces which are proper M-ideals. Studia Math. 81(1985), no. 2, 159–169.Google Scholar
[4] Chakerian, G. D. and Groemer, H., Convex bodies of constant width. In: Convexity and Its Applications, Birkhäuser, Basel, 1983, pp. 49–96.Google Scholar
[5] Dalla, L. and Tamvakis, N. K., Sets of constant width and diametrically complete sets in normed spaces. Bull. Soc. Math. Grèce (N.S.) 26(1985), 27–39.Google Scholar
[6] Day, M. M., Normed Linear Spaces. Third edition, Ergebnisse der Mathematik und ihrer Grenzgebiete 21, Springer–Verlag, Berlin, 1973.Google Scholar
[7] Eggleston, H. G., Convexity. Cambridge Tracts in Mathematics and Mathematical Physics 47, Cambridge University Press, New York, 1958.Google Scholar
[8] Eggleston, H. G., Sets of constant width in finite dimensional Banach spaces. Israel J. Math. 3(1965), 163–172.Google Scholar
[9] Fonf, V. and Lindenstrauss, J., Some results on infinite-dimensional convexity. Israel J. Math. 108(1998), 13–32.Google Scholar
[10] Franchetti, C., Relationship between the Jung constant and a certain projection constant in Banach spaces. Ann. Univ. Ferrara Sez. VII (N.S.) 23(1977), 39–44.Google Scholar
[11] Frolik, Z., Baire spaces and some generalizations of complete metric spaces. CzechoslovacMath. J. 11(86)(1961), 237–248.Google Scholar
[12] Granero, A. S., Moreno, J. P. and Phelps, R. R., Convex sets which are intersection of closed balls. Adv. Math. 183(2004), no. 1, 183–208.Google Scholar
[13] Groemer, H., On complete convex bodies. Geom. Dedicata 20(1986), no. 3, 319–334.Google Scholar
[14] Heil, E. and Martini, H., Special convex bodies. In: Handbook of Convex Geometry, Vol. A. North-Holland, Amsterdam, 1993, pp. 347–385.Google Scholar
[15] Jiménez Sevilla, M. and Moreno, J. P., A note on porosity and the Mazur intersection property. Mathematika, 47(2000), no. 1-2, 267–272.Google Scholar
[16] Jung, H. W. E., Über die kleinste Kügel, die eine räumlich Figur enschliesst. J. Reine Angew. Math. 123(1901), 241–257.Google Scholar
[17] Klee, V., Veselý, L. and Zanco, C., Rotundity and smoothness of convex bodies in reflexive and nonreflexive Banach spaces. Studia Math. 120(1996), no. 3, 191–204.Google Scholar
[18] Martini, H. and Swanepoel, K. J., The geometry of Minkowski spaces—A survey. Part II. Expos. Math. 22(2004), no. 2, 193–144.Google Scholar
[19] Moreno, J. P., Semicontinuous functions and convex sets in C(K) spaces. J. Austral.Math. Soc., to appear.Google Scholar
[20] Naszodi, M. and Visy, B., Sets with a unique extension to a set of constant width. In: Discrete Geometry, Monogr. Textbooks Pure Appl. Math. 253, Dekker, New York, 2003, pp. 373–380.Google Scholar
[21] Payá, R. and Rodríguez-Palacios, Á., Banach spaces which are semi-L-summands in their biduals. Math. Ann. 289(1991), no. 3, 529–542.Google Scholar
[22] Rodríguez-Palacios, Á., Infinite-dimensional sets of constant width and their applications. Extracta Math. Actas del II Congreso de Análisis Funcional, 1990, 140–151.Google Scholar
[23] Rodríguez-Palacios, Á., Properly semi-L-embedded complex spaces. Studia Math. 106(1993), no. 2, 197–202.Google Scholar
[24] Sallee, G. T., Preassigning the boundary of diametrically-complete sets. Monatsh.Math. 105(1988), no. 3, 217–227.Google Scholar
[25] Sallee, G. T., Sets of constant width, the spherical intersection property and circumscribed balls. Bull. Austral. Math. Soc. 33(1986), no. 3, 369–371.Google Scholar
[26] Yost, D., Irreducible convex sets. Mathematika 38(1991), no. 1, 134–155.Google Scholar
[27] Zajicek, L., Porosity and σ-porosity. Real Anal. Exchange 13(1987/88), no. 2, 314–350.Google Scholar
[28] Zanco, C. and Zucchi, A., Moduli of rotundity and smoothness for convex bodies. Boll. Un. Mat. Ital. B 7(1993), no. 4, 833–855.Google Scholar