Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-12T12:33:17.499Z Has data issue: false hasContentIssue false
  • English
  • Français

Derivations Tangential to Compact Group Actions: Spectral Conditions in the Weak Closure

Published online by Cambridge University Press:  20 November 2018

Ola Bratteli  and
Frederick M. Goodman
Ola Bratteli
Affiliation:
University of Trondheim, Trondheim, Norway
Frederick M. Goodman
Affiliation:
University of Iowa, Iowa City, Iowa
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a compact Lie group and a an action of G on a C*-algebra as *-automorphisms. Let 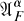denote the set of G-finite elements for this action, i.e., the set of those 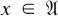such that the orbit {αg(x):g ∊ G} spans a finite dimensional space. 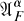is a common core for all the *-derivations generating one-parameter subgroups of the action α. Now let δ be a *-derivation with domain 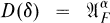such that 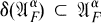Let us pose the following two problems:

  1. Is δ closable, and is the closure of δ the generator of a strongly continuous one-parameter group of *-automorphisms?

  2. If is simple or prime, under what conditions does δ have a decomposition

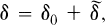
where 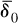is the generator of a one-parameter subgroup of α(G) and 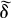is a bounded, or approximately bounded derivation?

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 1 , 01 February 1985 , pp. 160 - 192
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Araki, H., Haag, R., Kastler, D. and Takesaki, M., Extensions of states and chemical potential, Commun. Math. Phys. 53 (1977), 97–134.Google Scholar
2. Batty, C. J. K., Delays to flows on the real line, unpublished.Google Scholar
3. Bratteli, O. and Evans, D. E., Dynamical semigroups commuting with compact group actions, Ergod. Th. & Dynam. Sys. 3 (1983), 187–217.Google Scholar
4. Bratteli, O. and Evans, D. E., Derivations tangential to compact groups: The nonabelian case, preprint (1984).Google Scholar
5. Bratteli, O., Elliott, G. A. and Jorgensen, P. E. T., Decomposition of unbounded derivations into invariant and approximately inner parts, J. Reine Angew. Math. 346 (1984), 166–193.Google Scholar
6. Bratteli, O., Elliott, G. A. and Robinson, D. W., Strong topological transitivity and C*-dynamical systems, J. Math. Soc. Japan, to appear.CrossRefGoogle Scholar
7. Bratteli, O., Goodman, F. M. and Jorgensen, P. E. T., Unbounded derivations tangential to compact groups of automorphisms, II, J. Funct. Anal., to appear.CrossRefGoogle Scholar
8. Bratteli, O. and Jorgensen, P. E. T., Unbounded derivations tangential to compact groups of automorphisms, J. Funct. Anal. 48 (1982), 107–133.Google Scholar
9. Bratteli, O. and Jorgensen, P. E. T., Derivations commuting with abelian gauge actions on lattice systems, Commun. Math. Phys. 87 (1982), 353–364.Google Scholar
10. Bratteli, O., Jorgensen, P. E. T., Kishimoto, A. and Robinson, D. W., A C*-algebraic Schoenberg theorem, Ann. Inst. Fourier 34 (1984), in press.Google Scholar
11. Batty, C. J. K. and Kishimoto, A., Derivations and one-parameter sub-groups of C*-dynamical systems, preprint (1984).Google Scholar
12. Bratteli, O. and Robinson, D. W., Operator algebras and quantum statistical mechanics, Vol. I (1979) and Vol. II (1981) (Springer Verlag, New York-Heidelberg-Berlin).CrossRefGoogle Scholar
13. Christensen, E. and Evans, D. E., Cohomology of operator algebras and quantum dynamical semigroups, J. London Math. Soc. (2) 20 (1979), 353–368.Google Scholar
14. Christensen, E., Derivations and their relation to perturbation of operator algebras, Proc. Sympos. Pure Math. 38 (1982), 261–274.Google Scholar
15. Cuntz, J., Simple C*-algebras generated by isometries, Commun. Math., Phys. 57 (1977), 173–185.Google Scholar
16. Davies, E. B., A generation theorem for operators commuting with group actions, preprint (1983).Google Scholar
17. Glimm, J., On a certain class of operator algebras, Trans. Amer. Math. Soc. 95 (1960), 318–340.Google Scholar
18. Goodman, F. M. and Jorgensen, P. E. T., Unbounded derivations commuting with compact group actions, Commun. Math. Phys. 82 (1981), 399–405.Google Scholar
19. Kishimoto, A., Automorphisms and covariant irreducible representations, preprint (1983).Google Scholar
20. Kishimoto, A., Derivations with a domain condition, preprint (1984).Google Scholar
21. Kishimoto, A. and Robinson, D. W., Dissipations, derivations, dynamical systems, and asymptotic abelianness, preprint (1983).Google Scholar
22. Kishimoto, A. and Robinson, D. W., Derivations, dynamical systems, and spectral resolutions, preprint (1983).Google Scholar
23. Longo, R., Automatic relative boundedness of derivations in C*-algebras, J. Funct. Anal. 34 (1979), 21–28.Google Scholar
24. Longo, R. and Peligrad, C., Non-commutative topological dynamics and compact actions on C*-algebras, J. Funct. Anal. 58 (1984), 157–174.Google Scholar
25. Powers, R. T. and Price, G., Derivations vanishing on S(∞), Commun. Math. Phys. 84 (1982), 439–447.Google Scholar
26. Ringrose, J. R., Automatic continuity of derivations of operator algebras, J. London Math. Soc. (2) 5 (1972), 432–438.Google Scholar
27. Robinson, D. W., Stormer, E. and Takesaki, M., Derivations of simple C*-algebras tangential to compact automorphism groups, preprint (1983).Google Scholar
28. Sakai, S., C*-algebras and W*-algebras (Springer Verlag, New York-Heidelberg-Berlin, 1977).Google Scholar
29. Takesaki, M., Operator algebras and their automorphism groups, in Operator algebras and group representations, II (Pitman, Boston-London-Melbourne, 1984), 198–210.Google Scholar
30. Thomsen, K., A note to the previous paper by Bratteli, Goodman, and Jorgensen, J. Funct. Anal, to appear.Google Scholar