Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T06:44:59.093Z Has data issue: false hasContentIssue false
  • English
  • Français

Densities in certain three-way prime number races

Part of: Multiplicative number theory Probabilistic theory: distribution modulo $1$; metric theory of algorithms Zeta and $L$-functions: analytic theory Limit theorems Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  12 October 2020

Jiawei Lin  and
Greg Martin
Jiawei Lin
Affiliation:
Department of Mathematics, University of British Columbia Room 121, 1984 Mathematics Road, Vancouver, BC V6T 1Z2, Canada e-mail: [email protected]
Greg Martin*
Affiliation:
Department of Mathematics, University of British Columbia Room 121, 1984 Mathematics Road, Vancouver, BC V6T 1Z2, Canada e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

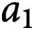Let $a_1$ , 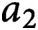$a_2$ , and 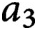$a_3$ be distinct reduced residues modulo q satisfying the congruences 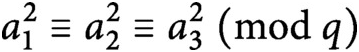$a_1^2 \equiv a_2^2 \equiv a_3^2 \ (\mathrm{mod}\ q)$ . We conditionally derive an asymptotic formula, with an error term that has a power savings in q, for the logarithmic density of the set of real numbers x for which 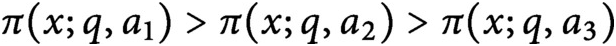$\pi (x;q,a_1)> \pi (x;q,a_2) > \pi (x;q,a_3)$ . The relationship among the 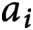$a_i$ allows us to normalize the error terms for the 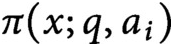$\pi (x;q,a_i)$ in an atypical way that creates mutual independence among their distributions, and also allows for a proof technique that uses only elementary tools from probability.

Keywords

Analytic number theoryprime number races

MSC classification

Primary: 11N13: Primes in progressions 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses 11K99: None of the above, but in this section
Secondary: 60F05: Central limit and other weak theorems 20E07: Subgroup theorems; subgroup growth
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 1 , February 2022 , pp. 232 - 265
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bacon, R. H., Approximations to multivariate normal orthant probabilities. Ann. Math. Stat. 34(1963), no. 1, 191–198.CrossRefGoogle Scholar
Bennett, M. A., Martin, G., O’Bryant, K., and Rechnitzer, A., Explicit bounds for primes in arithmetic progressions. Ill. J. Math. 62(2018), nos. 1–4, 427–532.Google Scholar
Fiorilli, D. and Martin, G., Inequities in the Shanks–Rényi prime number race: an asymptotic formula for the densities. J. Reine. Angew. Math. 2013(2013), no. 676, 121–212.CrossRefGoogle Scholar
Haber, S. and Rosenfeld, A., Groups as unions of proper subgroups. Am. Math. Mon. 66(1959), 491–494.CrossRefGoogle Scholar
Harper, A. J. and Lamzouri, Y., Orderings of weakly correlated random variables, and prime number races with many contestants. Probab. Theory Related Fields 170(2018), nos. 3–4, 961–1010.CrossRefGoogle Scholar
Hille, E. and Szegő, G., On the complex zeros of the Bessel functions. Bull. Am. Math. Soc. 49(1943), 605–610.CrossRefGoogle Scholar
Hurwitz, A., Ueber die Nullstellen der Bessel’schen Function. Math. Ann. 33(1888), no. 2, 246–266.CrossRefGoogle Scholar
Lamzouri, Y., The Shanks-Rényi prime number race with many contestants. Math. Res. Lett. 19 (2012), no. 3, 649–666.CrossRefGoogle Scholar
Lamzouri, Y., Prime number races with three or more competitors. Math. Ann. 356(2013), no. 3, 1117–1162.CrossRefGoogle Scholar
Martin, G., Asymmetries in the Shanks-Rényi prime number race. Number theory for the millennium, II (Urbana, IL, 2000), A. K. Peters, Natick, MA, 2002, pp. 403–415.Google Scholar
Rubinstein, M. and Sarnak, P., Chebyshev’s bias. Exp. Math. 3(1994), no. 3, 173–197.CrossRefGoogle Scholar
Szegő, G., Orthogonal polynomials. Vol. XXII. 4th ed., Amer. Math. Soc. Colloquium Publications, Providence, RI, 1975 Google Scholar
Watson, G. N., A treatise on the theory of Bessel functions. Cambridge Mathematical Library, Cambridge University Press, Cambridge, MA, 1995, Reprint of the second (1944) edition.Google Scholar
Zappa, G., The papers of Gaetano Scorza on group theory. Atti Accad. Naz. Lincei, Cl. Sci. Fis. Mat. Nat. IX. Ser. Rend. Lincei Mat. Appl. 2(1991), 95–101.Google Scholar