Article contents
Dense Subalgebras of Left Hilbert Algebras
Published online by Cambridge University Press: 20 November 2018
Extract
Let M be a von Neumann algebra acting on a Hilbert space 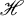 and assume that M has a separating and cyclic vector ω in
and assume that M has a separating and cyclic vector ω in 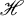 . Then it can happen that M contains a proper von Neumann subalgebra N for which ω is still cyclic. Such an example was given by Kadison in [4]. He considered
. Then it can happen that M contains a proper von Neumann subalgebra N for which ω is still cyclic. Such an example was given by Kadison in [4]. He considered 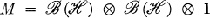 and
and 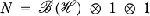 acting on
acting on 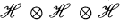 where
where 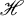 is a separable Hilbert space. In fact by a result of Dixmier and Maréchal, M, M′ and N have a joint cyclic vector [3]. Also Bratteli and Haagerup constructed such an example ([2], example 4.2) to illustrate the necessity of one of the conditions in the main result of their paper. In fact this situation seems to occur rather often in quantum field theory (see [1] Section 24.2, [3] and [4]).
is a separable Hilbert space. In fact by a result of Dixmier and Maréchal, M, M′ and N have a joint cyclic vector [3]. Also Bratteli and Haagerup constructed such an example ([2], example 4.2) to illustrate the necessity of one of the conditions in the main result of their paper. In fact this situation seems to occur rather often in quantum field theory (see [1] Section 24.2, [3] and [4]).
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1982
References
- 1
- Cited by


