Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T18:15:23.926Z Has data issue: false hasContentIssue false
  • English
  • Français

Dedekind Completeness and the Algebraic Complexity of o-Minimal Structures

Published online by Cambridge University Press:  20 November 2018

Alan Mekler ,
Matatyahu Rubin  and
Charles Steinhorn
Alan Mekler
Affiliation:
Department of Mathematics and Statistics Simon Fraser UniversityBurnaby B.C. V5AIS6
Matatyahu Rubin
Affiliation:
Department of Mathematics Ben Gurion University of the Negev Beer Sheva, Israel
Charles Steinhorn
Affiliation:
Department of Mathematics Vassar College Poughkeepsie, New York USA 12601
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An ordered structure is o-minimal if every definable subset is the union of finitely many points and open intervals. A theory is o-minimal if all its models are ominimal. All theories considered will be o-minimal. A theory is said to be n-ary if every formula is equivalent to a Boolean combination of formulas in n free variables. (A 2-ary theory is called binary.) We prove that if a theory is not binary then it is not rc-ary for any n. We also characterize the binary theories which have a Dedekind complete model and those whose underlying set order is dense. In [5], it is shown that if T is a binary theory, 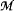is a Dedekind complete model of T, and I is an interval in 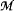, then for all cardinals K there is a Dedekind complete elementary extension 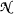of 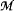, so that . In contrast, we show that if T is not binary and 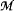is a Dedekind complete model of T, then there is an interval I in 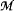so that if 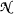is a Dedekind complete elementary extension of .

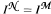Keywords

Primary: 03C07secondary: 03C65
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 44 , Issue 4 , 01 August 1992 , pp. 843 - 855
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Knight, J., Pillay, A. and Steinhorn, C., Definable sets in ordered structures II, Trans. Amer. Math. Soc. 295 (1986),593–605.Google Scholar
2. Marker, D., Omitting types in o-minimal theories, Journal of Symbolic Logic 51 (1986), 63–74.Google Scholar
3. Pillay, A., Some remarks on definable equivalence relations in o-minimal structures, Journal of Symbolic Logic 51 (1986), 709–714.Google Scholar
4. Pillay, A. and Steinhorn, C., Definable sets in ordered structures I, Trans. Amer. Math. Soc. 295 (1986), 565–592.Google Scholar
5. Pillay, A. and Steinhorn, C., On Dedekind complete o-minimal structures, Journal of Symbolic Logic 52 (1987), 156–164.Google Scholar