Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-30T21:19:16.374Z Has data issue: false hasContentIssue false
  • English
  • Français

Decompositions of the Hilbert Function of a Set of Points in ℙn

Published online by Cambridge University Press:  20 November 2018

Anthony V. Geramita ,
Tadahito Harima  and
Yong Su Shin
Anthony V. Geramita
Affiliation:
Department of Mathematics, Queen's University, Kingston, Ontario, K7L 3N6 and Dipartimento di Matematica, Universitá di Genova, Genova, Italia. email: [email protected], [email protected]
Tadahito Harima
Affiliation:
Department of Management and Information Science, Shikoku University, Tokushima 771-11, Japan. email: [email protected]
Yong Su Shin
Affiliation:
Department of Mathematics, Sung Shin Women's University, 249-1, Dong Sun Dong 3Ka, Sung Buk Ku, Seoul, Korea 136-742. email: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

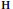Let $\mathbf{H}$ be the Hilbert function of some set of distinct points in 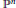${{\mathbb{P}}^{n}}$ and let 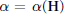$\alpha \,=\,\alpha (\mathbf{H})$ be the least degree of a hypersurface of 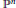${{\mathbb{P}}^{n}}$ containing these points. Write 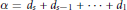$\alpha ={{d}_{s}}+{{d}_{s-1}}+\cdot \cdot \cdot +{{d}_{1}}$ (where 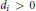${{d}_{i}}>0$ ). 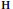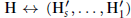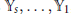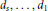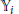We canonically decompose $\mathbf{H}$ into $s$ other Hilbert functions $\text{H}\leftrightarrow \text{(}{{\text{H}'}_{s}}\text{,}...\text{,}{{\text{H}'}_{1}}\text{)}$ and show how to find sets of distinct points ${{\mathbb{Y}}_{s}},...,{{\mathbb{Y}}_{1}}$ , lying on reduced hypersurfaces of degrees ${{d}_{s}},...,{{d}_{1}}$ (respectively) such that the Hilbert function of ${{\mathbb{Y}}_{i}}$ is 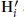${{\text{H'}}_{i}}$ and the Hilbert function of $\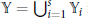mathbb{Y}=\bigcup _{i=1}^{s}\,{{\mathbb{Y}}_{i}}$ is 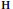$\mathbf{H}$. Some extremal properties of this canonical decomposition are also explored.

Keywords

13D4014M10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 5 , 01 October 2001 , pp. 923 - 943
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Bigatti, A., Geramita, A. V. and Migliore, J., Geometric Consequences of Extremal Behavior in a Theorem of Macaulay. Trans. Amer.Math. Soc. (1) 346(1994), 203–235.Google Scholar
[2] Geramita, A. V., Gregory, D. and Roberts, L., Monomial Ideals and Points in Projective Space. J. Pure Appl. Algebra 40(1986), 33–62.Google Scholar
[3] Geramita, A. V., Harima, T. and Shin, Y. S., An Alternative to the Hilbert Function for the Ideal of a Finite Set of Points in ℙ n . Illinois J. Math., to appear.Google Scholar
[4] Geramita, A. V., Harima, T. and Shin, Y. S., Extremal Point Sets and Gorenstein Ideals. Adv. Math. 152(2000), 78–119.Google Scholar
[5] Geramita, A. V., Maroscia, P. and Roberts, L., The Hilbert function of a reduced K-algebra. J. London Math. Soc. 28(1983), 443–452.Google Scholar
[6] Geramita, A. V., Pucci, M. and Shin, Y. S., Smooth Points of . J. Pure Appl. Algebra 122(1997), 209–241.Google Scholar
[7] Geramita, A. V. and Shin, Y. S., k-configurations in ℙ3 All Have Extremal Resolutions. J. Algebra 213(1999), 351–368.Google Scholar
[8] Gruson, L. and Peskine, C., Genre des Courbes de L’Espace projectif. In: Algebraic Geometry, Lecture Notes in Math. 687, Springer, 1978.Google Scholar
[9] Harima, T., Some Examples of unimodal Gorenstein sequences. J. Pure Appl. Algebra 103(1995), 313–324.Google Scholar
[10] Roberts, L. and Roitman, M., On Hilbert Function of Reduced and of Integral Algebra. J. Pure Appl. Algebra 56(1989), 85–104.Google Scholar
[11] Stanley, R., Hilbert Functions of Graded Algebras. Adv. Math. 28(1978), 57–83.Google Scholar