Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-14T05:17:50.057Z Has data issue: false hasContentIssue false
  • English
  • Français

Decay of Mean Values of Multiplicative Functions

Published online by Cambridge University Press:  20 November 2018

Andrew Granville  and
K. Soundararajan
Andrew Granville
Affiliation:
Départment de Mathématiques, et Statistique, Université de Montréal, CP 6128 succ Centre-Ville, Montréal, Québec, H3C 3J7 e-mail: [email protected]
K. Soundararajan
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, Michigan 48109, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

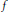For given multiplicative function $f$, with 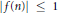$\left| f\left( n \right) \right|\le 1$ for all $n$, we are interested in how fast its mean value 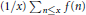$\left( 1/x \right)\sum{_{n\le x}f\left( n \right)}$ converges. Halász showed that this depends on the minimum 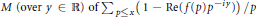$M\,\left( \text{over}\,y\,\in \,\mathbb{R} \right)\,\text{of}\,\sum{_{p\le x}\left( 1-\operatorname{Re}\left( f\left( p \right){{p}^{-iy}} \right) \right)}/p$, and subsequent authors gave the upper bound 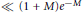$\ll \left( 1+M \right){{e}^{-M}}$. For many applications it is necessary to have explicit constants in this and various related bounds, and we provide these via our own variant of the Halász-Montgomery lemma (in fact the constant we give is best possible up to a factor of 10). We also develop a new type of hybrid bound in terms of the location of the absolute value of $y$ that minimizes the sum above. 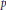As one application we give bounds for the least representatives of the cosets of the $k$-th powers mod $p$.

Keywords

11N6011N5610K2011N37
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 6 , 01 December 2003 , pp. 1191 - 1230
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Bonnesen, T. and Fenchel, W., Theorie der konvexen Körper. Chelsea, New York, 1949.Google Scholar
[2] Davenport, H. and Erdős, P., The distribution of quadratic and higher residues. Publ. Math. Debrecen 2(1952), 252–265.Google Scholar
[3] Elliott, P. D. T. A., Extrapolating the mean-values of multiplicative functions. Indag. Math 51(1989), 409–420.Google Scholar
[4] Elliott, P. D. T. A., Some remarks about multiplicative functions of modulus ≤ 1 . In: Analytic number theory, Allerton Park, IL, 1989, Progr. Math 85, Birkhäuser Boston, Boston, MA, 1990, 159–164.Google Scholar
[5] Goldston, D. A. and McCurley, K. S., Sieving the positive integers by large primes. J. Number Theory 28(1988), 94–115.Google Scholar
[6] Granville, A. and Soundararajan, K., The spectrum of multiplicative functions. Ann. of Math. 153(2001), 407–470.Google Scholar
[7] Granville, A. and Soundararajan, K., An upper bound for the unsieved integers up to x. to appear.Google Scholar
[8] Halász, G., On the distribution of additive and mean-values of multiplicative functions. Studia Sci. Math. Hungar. 6(1971), 211–233.Google Scholar
[9] Halász, G., On the distribution of additive arithmetic functions. Acta Arith. 27(1975), 143–152.Google Scholar
[10] Halberstam, H. and Richert, H.-E., On a result of R. R. Hall. J. Number Theory 11(1979) 76–89.Google Scholar
[11] Hall, R. R., Halving an estimate obtained from Selberg's upper bound method. Acta Arith. 25(1974), 347–351.Google Scholar
[12] Hall, R. R., A sharp inequality of Halász type for the mean value of a multiplicative arithmetic function. Mathematika 42(1995), 144–157.Google Scholar
[13] Hall, R. R. and Tenenbaum, G., Effective mean value estimates for complex multiplicative functions. Math. Proc. Cambridge Philos. Soc. 110(1991), 337–351.Google Scholar
[14] Hildebrand, A., A note on Burgess's character sum estimate. C. R. Math. Acad. Sci. Soc. R. Can. 8(1986), 35–37.Google Scholar
[15] Montgomery, H. L., A note on the mean values of multiplicative functions. Inst. Mittag-Lefèr, Report 17.Google Scholar
[16] Montgomery, H. L. and Vaughan, R. C., Hilbert's inequality. J. LondonMath. Soc. (2) 8(1974), 73–82.Google Scholar
[17] Montgomery, H. L. and Vaughan, R. C., Mean-values of multiplicative functions. Period. Math. Hungar. 43(2001), 188–214.Google Scholar
[18] Tenenbaum, G., Introduction to analytic and probabilistic number theory. Cambridge University Press, 1995.Google Scholar
[19] Wintner, A., The theory of measure in arithmetical semigroups. Baltimore, 1944.Google Scholar
[20] Wirsing, E., Das asymptotische Verhalten von Summen über multiplikative Funktionen II. Acta Math. Acad. Sci. Hungar. 18(1967), 411–467.Google Scholar