Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T03:37:59.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Cyclic Cohomology of Non-Commutative Tori

Published online by Cambridge University Press:  20 November 2018

Ryszard Nest
Ryszard Nest*
Affiliation:
University of Copenhagen, Copenhagen, Denmark
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we shall compute the cyclic cohomology of a non-commutative torus, i.e., a certain algebra 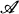associated with an antisymmetric bicharacter of a finite rank free abelian group G.

The main result is

1.1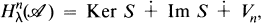

where

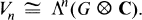
The method of computation generalises the computation of the cyclic cohomology of the irrational rotation algebras given by Connes in [3]. (Our method works equally well also in the rational case, which was dealt with by a different method by Connes in [3].)

We first describe the Hochschild cohomology of 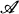in an explicit way, and then combine this description with the exact sequence of [3]:

1.2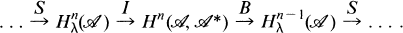

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 5 , 01 October 1988 , pp. 1046 - 1057
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Bratteli, O., Elliott, G. A. and Jørgensen, P. E. T., Decomposition of unbounded derivations into invariant and approximately inner parts, J. Reine Angew, Math. 346 (1984), 166–193.Google Scholar
2. Brenken, B., Cuntz, J., Elliott, G. A. and Nest, R., On the classification of noncommutative tori, III, Operator Algebras and Mathematical Physics, Contemporary Mathematics 62 (Amer. Math. Soc, 1987), 503–526.Google Scholar
3. Connes, A., Non-commutative differential geometry, Inst. Hautes Etudes Sci. Publ. Math. 62 (1985), 257–360.Google Scholar
4. Connes, A., Cyclic cohomology and the transverse class of a foliation, Geometric Methods in Operator Algebras (Longman, London, 1986), 52–144.Google Scholar
5. Cuntz, J., Elliott, G. A., Goodman, F. M. and Jørgensen, P. E. T., On the classification of noncommutative tori, II, C.R. Math. Rep. Acad. Sci. Canada 8 (1985), 189–194.Google Scholar
6. Disney, S., Elliott, G. A., Kumjian, A. and Raeburn, I., On the classification of noncommutative tori, C.R. Math. Rep. Acad. Sci. Canada 7 (1985), 137–141.Google Scholar
7. Elliott, G. A., On the K-theory of the C*-algebra generated by a projective representation of a torsion-free discrete abelian group, Operator Algebras and Group Representations, Volume 1 (Pitman, London, 1984), 157–184.Google Scholar
8. Nest, R., Cyclic cohomology of crossed products with Z, J. Funct. Anal., in press.Google Scholar