Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T06:57:07.409Z Has data issue: false hasContentIssue false
  • English
  • Français

Cycle-Level Intersection Theory for Toric Varieties

Published online by Cambridge University Press:  20 November 2018

Hugh Thomas
Hugh Thomas*
Affiliation:
The Fields Institute, 222 College St., Toronto, ON, M5T 3J1 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper addresses the problem of constructing a cycle-level intersection theory for toric varieties. We show that by making one global choice, we can determine a cycle representative for the intersection of an equivariant Cartier divisor with an invariant cycle on a toric variety. 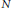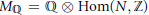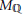For a toric variety defined by a fan in $N$, the choice consists of giving an inner product or a complete flag for ${{M}_{\mathbb{Q}}}\,=\,\mathbb{Q}\,\otimes \,\text{Hom(}N,\,\mathbb{Z}\text{)}$ , or more generally giving for each cone σ in the fan a linear subspace of ${{M}_{\mathbb{Q}}}$ complementary to 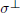${{\sigma }^{\bot }}$ , satisfying certain compatibility conditions. We show that these intersection cycles have properties analogous to the usual intersections modulo rational equivalence. If 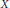$X$ is simplicial (for instance, if 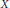$X$ is non-singular), we obtain a commutative ring structure to the invariant cycles of 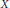$X$ with rational coefficients. This ring structure determines cycles representing certain characteristic classes of the toric variety. We also discuss how to define intersection cycles that require no choices, at the expense of increasing the size of the coefficient field.

Keywords

14M2514C17toric varietiesintersection theory
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 5 , 01 October 2004 , pp. 1094 - 1120
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Danilov, V. I., The geometry of toric varieties. Russian Math. Surveys 33(1978), 97–154; Uspekhi Mat. Nauk 33(1978), 85–134.Google Scholar
[2] Diaconis, P. and Fulton, W., A growth model, a game, an algebra, Lagrange inversion, and characteristic classes. Rend. Sem. Math. Univ. Politec. Torino 49(1991), 95–119.Google Scholar
[3] Fulton, W., Intersection theory. Ergebnisse der Mathematik und ihrer Grenzgebiete 3, Springer-Verlag, Berlin, 1984.Google Scholar
[4] Fulton, W., Introduction to toric varieties. Annals of Mathematics Studies 131, Princeton University Press, Princeton, NJ, 1993.Google Scholar
[5] Fulton, W. and Sturmfels, B., Intersection theory on toric varieties. Topology 36(1997), 335–353.Google Scholar
[6] Morelli, R., Pick's theorem and the Todd class of a toric variety. Adv. Math. 100(1993), 183–231.Google Scholar
[7] Pommersheim, J., Products of Cycles and the Todd Class of a Toric Variety. J. Amer. Math. Soc. 9(1996), 813–826.Google Scholar
[8] Pommersheim, J. and Thomas, H., Cycles representing the Todd class of a toric variety. J. Amer. Math. Soc. (to appear).Google Scholar
[9] Stanley, R., Combinatorics and commutative algebra. Second edition, Progress in Mathematics 41, Birkhäuser, Boston, MA, 1996.Google Scholar
[10] Thomas, H., An action of equivariant Cartier divisors on invariant cycles for toric varieties. Ph.D. Thesis, University of Chicago, 2000.Google Scholar
[11] Thomas, H., Order-preserving maps from a poset to a chain, the order polytope, and the Todd class of the associated toric variety. European J. Combin. 24(2003), 809–814.Google Scholar
[12] Wilf, H., generating functionology. Academic Press, Boston, MA, 1990.Google Scholar