Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-19T00:27:23.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Curvature Bounds for Surfaces in Hyperbolic 3-Manifolds

Published online by Cambridge University Press:  20 November 2018

William Breslin
William Breslin*
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI, U.S.A.
*
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A triangulation of a hyperbolic 3-manifold is 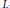$L$-thick if each tetrahedron having all vertices in the thick part of 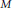$M$ is 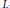$L$-bilipschitz diffeomorphic to the standard Euclidean tetrahedron. We show that there exists a fixed constant 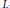$L$ such that every complete hyperbolic 3-manifold has an 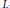$L$-thick geodesic triangulation. We use this to prove the existence of universal bounds on the principal curvatures of 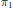${{\pi }_{1}}$-injective surfaces and strongly irreducible Heegaard surfaces in hyperbolic 3-manifolds.

Keywords

57M50
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 5 , 01 October 2010 , pp. 994 - 1010
Copyright
Copyright © Canadian Mathematical Society 2010

Footnotes

This work was partially supported by the NSF grant DMS-0135345.

References

[Bre] Breslin, W. G., Thick triangulations of hyperbolic n-manifolds. Pacific J. Math. 241(2009), no. 2, 215–225. doi:10.2140/pjm.2009.241.215Google Scholar
[EL M+00] Edelsbrunner, H., Li, X.-Y., Miller, G., Stathopoulos, A., Talmor, D., Teng, S.-H., Unger, A., and Walkington, N., Smoothing and cleaning up slivers. In: Proceedings of the Thirty-Second Annual AC M Symposium on Theory of Computing, AC M, New York, 2000, pp. 273–277.Google Scholar
[Fen89] Fenchel, W., Elementary geometry in hyperbolic space. de Gruyter Studies in Mathematics, 11, Walter de Gruyter & Co., Berlin, 1989.Google Scholar
[FHS83] Freedman, M., Hass, J., and Scott, P., Least area incompressible surfaces in 3-manifolds. Invent. Math. 71(1983), no. 3, 609–642. doi:10.1007/BF02095997Google Scholar
[Hak61] Haken, W., Ein Verfahren zur Aufspaltung einer 3-Mannigfaltigkeit in irreduzible 3-Mannigfaltigkeiten. Math. Z. 76(1961), 427–467. doi:10.1007/BF01210988Google Scholar
[K M68] Kazdan, D. and Margulis, G. A., A proof of Selberg's hypothesis. Math. Sb. 75(1968), 163–168.Google Scholar
[Li00] Li, X.-Y., Spacing control and sliver-free Delaunay mesh. In: Proceedings, 9th International Meshing Roundtable, Sandia National Laboratories, 2000, pp. 295–306. http://www.imr.sandia.gov/papers/imr9/li00.ps.gz Google Scholar
[LL00] Leibon, G. and Letscher, D., Delaunay triangulations and Voronoi diagrams for Riemannian manifolds. In: Proceedings of the Sixteenth Annual Symposium on Computational Geometry (Hong Kong, 2000), AC M, New York, 2000, pp. 341–349.Google Scholar
[MTTW96] G.L. Miller, Talmor, D., S.H. Teng, and H.Walkington, and N.Wang, Control volume meshes using sphere packing: generation refinement, and coarsening, Proceedings, 5th International Meshing Roundtable, Sandia National Laboratories, 1996, pp. 47–61. http://www.imr.sandia.gov/papers/imr5/miller-final2631.ps.gz Google Scholar
[Rub97] Rubinstein, J. H., Polyhedral minimal surfaces, Heegaard splittings and decision problems for 3-dimensional manifolds. In: Geometric topology (Athens, GA, 1993), American Mathematical Society, Providence, RI, 1997, pp. 1–20.Google Scholar
[Sau05] Saucan, E., Note on a theorem of Munkres. Mediterr. J. Math. 2(2005), no. 2, 215–229. doi:10.1007/s00009-005-0040-zGoogle Scholar
[Sau06a] Saucan, E., The existence of quasimeromorphic mappings. Ann. Acad. Sci. Fenn. Math. 31(2006), no. 1, 131–142.Google Scholar
[Sau06b] Saucan, E., The existence of quasimeromorphic mappings in dimension 3. Conform. Geom. Dyn. 10(2006), 21–40. doi:10.1090/S1088-4173-06-00111-1Google Scholar
[Sch83] Schoen, R., Estimates for stable minimal surfaces in three-dimensional manifolds. In: Seminar on minimal submanifolds, Ann.of Math. Stud., 103, Princeton University Press, Princeton, NJ, 1983, pp. 111–126.Google Scholar
[Sto00] Stocking, M., Almost normal surfaces in 3-manifolds. Trans. Amer. Math. Soc. 352(2000), no. 1, 171–207. doi:10.1090/S0002-9947-99-02296-5Google Scholar
[SY79] Schoen, R. and Yau, S. T., Existence of incompressible minimal surfaces and the topology of three-dimensional manifolds with nonnegative scalar curvature. Ann. of Math. 110(1979), no. 1, 127–142. doi:10.2307/1971247Google Scholar