Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T16:04:36.828Z Has data issue: false hasContentIssue false
  • English
  • Français

The Cubic Dirac Operator for Infinite-Dimensonal Lie Algebras

Published online by Cambridge University Press:  20 November 2018

Eckhard Meinrenken
Eckhard Meinrenken*
Affiliation:
University of Toronto, Department of Mathematics, 40 St. George Street, Toronto, ON M5S 2E4 email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 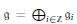$\mathfrak{g}\,=\,{{\oplus }_{i\in \mathbb{Z}}}{{\mathfrak{g}}_{i}}$ be an infinite-dimensional graded Lie algebra, with dim 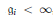${{\mathfrak{g}}_{i}}\,<\,\infty $, equipped with a non-degenerate symmetric bilinear form 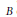$B$ of degree 0. The quantum Weil algebra 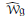${{\hat{\mathcal{W}}}_{\mathfrak{g}}}$ is a completion of the tensor product of the enveloping and Clifford algebras of 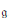$\mathfrak{g}$. Provided that the Kac–Peterson class of 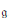$\mathfrak{g}$ vanishes, one can construct a cubic Dirac operator 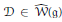$\mathcal{D}\,\in \,\hat{\mathcal{W}}(\mathfrak{g})$, whose square is a quadratic Casimir element. We show that this condition holds for symmetrizable Kac– Moody algebras. Extending Kostant's arguments, one obtains generalized Weyl–Kac character formulas for suitable “equal rank” Lie subalgebras of Kac–Moody algebras. These extend the formulas of G. Landweber for affine Lie algebras.

Keywords

22E6515A66
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 6 , 01 December 2011 , pp. 1364 - 1387
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Alekseev, A. and Meinrenken, E., The non-commutative Weil algebra. Invent. Math. 139(2000), no. 1, 135–172. doi:10.1007/s002229900025Google Scholar
[2] Gross, B., Kostant, B., Ramond, P., and Sternberg, S., The Weyl character formula, the half-spin representations, and equal rank subgroups. Proc. Natl. Acad. Sci. USA 95(1998), no. 15, 8441–8442 (electronic). doi:10.1073/pnas.95.15.8441Google Scholar
[3] Guillemin, V. and Sternberg, S., Symplectic techniques in physics. Cambridge Univ. Press, Cambridge, 1990.Google Scholar
[4] Kac, V., Infinite-dimensional Lie algebras and Dedekind's eta-function. (Russian) Funkcional. Anal. i Prilozen. 8(1974), no. 1, 77–78.Google Scholar
[5] Kac, V., Infinite-dimensional Lie algebras. Second ed., Cambridge University Press, Cambridge, 1985.Google Scholar
[6] Kac, V. and Peterson, D., Spin and wedge representations of infinite-dimensional Lie algebras and groups. Proc. Nat. Acad. Sci. U.S.A. 78(1981), no. 6, part 1, 3308–3312. doi:10.1073/pnas.78.6.3308Google Scholar
[7] Kac, V. and Todorov, T., Superconformal current algebras and their unitary representations. Comm. Math. Phys. 102(1985), no. 2, 337–347. doi:10.1007/BF01229384Google Scholar
[8] Kazama, Y. and Suzuki, H., Characterization of n = 2 superconformal models generated by the coset space method. Phys. Lett. B 216(1989), no. 1–2, 112–116. doi:10.1016/0370-2693(89)91378-6Google Scholar
[9] Kitchloo, N., Dominant K-theory and integrable highest weight representations of Kac-Moody groups. Adv. Math. 221(2009), no. 4, 1191–1226. doi:10.1016/j.aim.2009.02.006Google Scholar
[10] Kostant, B., A cubic Dirac operator and the emergence of Euler number multiplets of representations for equal rank subgroups. Duke Math. J. 100(1999), no. 3, 447–501. doi:10.1215/S0012-7094-99-10016-0Google Scholar
[11] Kostant, B., A generalization of the Bott-Borel-Weil theorem and Euler number multiplets of representations. In: Conference Moshé Flato 1999, vol. 1, Math. Phys. Stud., 21, Kluwer Acad. Publ., Dordrecht, 2000, pp. 309–325.Google Scholar
[12] Kostant, B. and Sternberg, S., Symplectic reduction, BRS cohomology, and infinite-dimensional Clifford algebras. Ann. Phys. 176(1987), no. 1, 49–113. doi:10.1016/0003-4916(87)90178-3Google Scholar
[13] Kumar, S., Kac–Moody groups, their flag varieties and representation theory. Progress in Mathematics, 204, Birkhäuser Boston Inc., Boston, MA, 2002.Google Scholar
[14] Landweber, G., Multiplets of representations and Kostant's Dirac operator for equal rank loop groups. Duke Math. J. 110(2001), no. 1, 121–160. doi:10.1215/S0012-7094-01-11014-4Google Scholar
[15] Medina, A. and Revoy, Ph., Caractérisation des groupes de Lie ayant une pseudo-métrique bi-invariante. Applications. In: South Rhone seminar on geometry, III (Lyon, 1983), Travaux en Cours, Hermann, Paris, 1984, pp. 149–166.Google Scholar
[16] Meinrenken, E., Lie groups and Clifford algebras, Lecture notes, http://www.math.toronto.edu/mein/teaching/lectures.html.Google Scholar
[17] Morita, J., Certain rank two subsystems of Kac-Moody root systems. In: Infinite-dimensional Lie algebras and groups (Luminy-Marseille, 1988), Adv. Ser. Math. Phys., 7, World Sci. Publ., Teaneck, NJ, 1989, pp. 52–56.Google Scholar
[18] Naito, S., On regular subalgebras of Kac-Moody algebras and their associated invariant forms. Symmetrizable case. J. Math. Soc. Japan 44(1992), no. 2, 157–177. doi:10.2969/jmsj/04420157Google Scholar
[19] Wassermann, A., Kac–Moody algebras and Virasoro algebras, lecture notes. 1998. arxiv:1004.1287Google Scholar