Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Berndt, Bruce C.
Bhargava, S.
and
Garvan, Frank G.
1995.
Ramanujan’s theories of elliptic functions to alternative bases.
Transactions of the American Mathematical Society,
Vol. 347,
Issue. 11,
p.
4163.
Liu, Zhi-Guo
2000.
Some Eisenstein Series Identities.
Journal of Number Theory,
Vol. 85,
Issue. 2,
p.
231.
Liu, Zhi-Guo
2001.
Symbolic Computation, Number Theory, Special Functions, Physics and Combinatorics.
Vol. 4,
Issue. ,
p.
147.
Hirschhorn, Michael D.
2001.
The Andrews Festschrift.
p.
159.
Cooper, Shaun
2003.
Cubic theta functions.
Journal of Computational and Applied Mathematics,
Vol. 160,
Issue. 1-2,
p.
77.
Liu, Zhi-Guo
2004.
A theta function identity and its implications.
Transactions of the American Mathematical Society,
Vol. 357,
Issue. 2,
p.
825.
Choie, YoungJu
and
Solé, Patrick
2004.
Ternary codes and Jacobi forms.
Discrete Mathematics,
Vol. 282,
Issue. 1-3,
p.
81.
Cooper, S.
and
Hirschhorn, M.D.
2004.
Results of Hurwitz type for three squares.
Discrete Mathematics,
Vol. 274,
Issue. 1-3,
p.
9.
Cooper, Shaun
2005.
A simple proof of an expansion of an eta-quotient as a Lambert series.
Bulletin of the Australian Mathematical Society,
Vol. 71,
Issue. 3,
p.
353.
Berkovich, Alexander
and
Garvan, Frank
2005.
On the Andrews-Stanley refinement of Ramanujan’s partition congruence modulo 5 and generalizations.
Transactions of the American Mathematical Society,
Vol. 358,
Issue. 2,
p.
703.
Chapman, Robin
2005.
Cubic Identities for Theta Series in Three Variables.
The Ramanujan Journal,
Vol. 8,
Issue. 4,
p.
459.
2006.
The Mathematica GuideBook for Symbolics.
p.
978.
Cooper, Shaun
2006.
Cubic elliptic functions.
The Ramanujan Journal,
Vol. 11,
Issue. 3,
p.
355.
Hirschhorn, Michael D.
and
Sellers, James A.
2007.
On recent congruence results of Andrews and Paule for broken k-diamonds.
Bulletin of the Australian Mathematical Society,
Vol. 75,
Issue. 1,
p.
121.
Liu, Zhi-Guo
2007.
An addition formula for the Jacobian theta function and its applications.
Advances in Mathematics,
Vol. 212,
Issue. 1,
p.
389.
Cooper, Shaun
and
Toh, Pee Choon
2008.
Determinant identities for theta functions.
Journal of Mathematical Analysis and Applications,
Vol. 347,
Issue. 1,
p.
1.
Berkovich, Alexander
and
Garvan, Frank G.
2008.
K. Saito's Conjecture for nonnegative eta products and analogous results for other infinite products.
Journal of Number Theory,
Vol. 128,
Issue. 6,
p.
1731.
Hirschhorn, Michael D.
2008.
A Letter from Fitzroy House.
The American Mathematical Monthly,
Vol. 115,
Issue. 6,
p.
563.
Zeng, Xian-Feng
2009.
A generalized circular summation of theta function and its application.
Journal of Mathematical Analysis and Applications,
Vol. 356,
Issue. 2,
p.
698.
HIRSCHHORN, MICHAEL D.
and
SELLERS, JAMES A.
2009.
ELEMENTARY PROOFS OF VARIOUS FACTS ABOUT 3-CORES.
Bulletin of the Australian Mathematical Society,
Vol. 79,
Issue. 3,
p.
507.


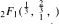 analogous to the classical
analogous to the classical 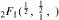 We give elliptic function generalizations of
We give elliptic function generalizations of 