Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-20T08:12:05.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Criteria for σ-Smoothness, τ-Smoothness, and Tightness of Lattice Regular Measures, with Applications

Published online by Cambridge University Press:  20 November 2018

George Bachman  and
Panagiotis D. Stratigos
George Bachman
Affiliation:
Polytechnic Institute of New York, Brooklyny New York
Panagiotis D. Stratigos
Affiliation:
Long Island University, Brooklyn, New York
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider an arbitrary set X and an arbitrary disjunctive lattice of subsets of X, ℒ. The algebra of subsets of X generated by ℒ is denoted by 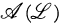, the set of all ℒ-regular measures on 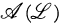, by MR(ℒ), and the associated Wallman space, a compact T1 space, by IR(ℒ); assume X is embedded in IR(ℒ) (otherwise, consider the image of X in IR(ℒ)).

In part of an earlier paper [4] the work of Knowles [15] and Gould and Mahowald [11] was generalized from the explicit topological setting of X, a Tychonoff space, with ℒ the lattice of zero sets of X, to the above setting, with the added assumption that ℒ was also δ and normal. This was done so that the important Alexandroff Representation Theorem [1] could be utilized in order to induce two associated measures 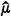, and 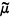defined on 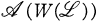and 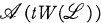respectively, where W(ℒ) is the Wallman lattice in IR(ℒ).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 6 , 01 December 1981 , pp. 1498 - 1525
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Alexandroff, A. D., Additive set junctions in abstract spaces, Mat. Sb. (N.S.), 9 51 (1941), 563–628.Google Scholar
2. Bachman, G. and Hsu, P., Extensions of lattice continuous maps to generalized Wallman spaces, Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. 62 (1977), 107–114.Google Scholar
3. Bachman, G. and Sultan, A., Extensions of regular lattice measures with topological applications, J. Math. Anal, and Appl. 57 (1977), 539–559.Google Scholar
4. Bachman, G. and Sultan, A., Representations of linear junctionals on spaces of continuous functions, repletions, and general measure extensions, J. Math. Anal, and Appl. 67 (1979), 277–293.Google Scholar
5. Bachman, G. and Sultan, A., On regular extensions of measures, Pacific J. Math. 86 (1980), 389–395.Google Scholar
6. Banaschewski, B., Uber nulldimensionale Raume, Math. Nachr. 13 (1955), 129–140.Google Scholar
7. Dugundji, J., Topology, (Allyn and Bacon, Boston, 1966).Google Scholar
8. Dykes, N., Generalizations of realcompact spaces, Pacific J. Math. 33 (1970), 571–581.Google Scholar
9. Engelking, R., Outline of general topology, (North-Holland Publishing Co., Amsterdam, New York, 1968).Google Scholar
10. Gillman, L. and Jerrison, M., Rings of continuous functions, (Van Nostrand, Princeton, N.J., 1960).Google Scholar
11. Gould, G. G. and Mahowald, M., Measures on completely regular spaces, J. London Math. Soc. 37 (1962), 103–111.Google Scholar
12. Hager, A., Reynolds, G. and Rice, M., Borel complete topological spaces, Fund. Math. 75 (1972), 135–143.Google Scholar
13. Halmos, P., Measure theory, (Van Nostrand, Toronto, New York, London, 1950).Google Scholar
14. Herrlich, H., E-Kompacte Raume, Math. Zeit. 96 (1967), 228–255.Google Scholar
15. Knowles, J., Measures on topological spaces, Proc. London Math. Soc. 17 (1967), 139–156.Google Scholar
16. Lembcke, J., Konservative Abbildungen und Forlsetzung regularer Masse, Z. Wahr. 15 (1970), 57–96.Google Scholar
17. Moran, W., Measures and mappings on topological spaces, Proc. London Math. Soc. 19 (1969), 493–508.Google Scholar
18. Sultan, A., Measure compactification and representation, Can. J. Math. 30 (1978), 54–65.Google Scholar
19. Szeto, M., Measure repleteness and mapping preservations, (to appear in J. Indian Math. Soc).Google Scholar
20. Topsøe, F., Topology and measure, Springer Lecture Notes 133 (Springer-Verlag, Berlin, Heidelberg, New York, 1970).Google Scholar
21. Varadarajan, V., Measures on topological spaces, Amer. Math. Soc. Trans., Ser. 2 48 (1965), 161–228.Google Scholar
22. Wallman, H., Lattices and topological spaces, Ann. of Math. 42 (1938), 687–697.Google Scholar
23. Yosida, K. and Hewitt, E., Finitely additive measures, Trans. Amer. Math. Soc. 72 (1952), 46–66.Google Scholar
24. Zaanen, A., An Introduction to the theory of integration, (North-Holland Publishing Co., Amsterdam, New York, 1958).Google Scholar