No CrossRef data available.
Article contents
Counterexample to a Conjecture on Positive Definite Functions
Published online by Cambridge University Press: 20 November 2018
Extract
Cooper [1] called a complex-valued function f on the real line Rpositive definite for F, where F is a set of complex-valued functions on R, if the integral
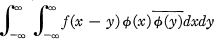
exists as a Lebesgue integral and is nonnegative for every ϕ in F. Let us denote by P(F) the set of functions positive definite for F, by 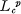 the set of functions in LP(R) with compact support, and by
the set of functions in LP(R) with compact support, and by 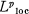 the set of functions which are locally in LP(R), i.e.,
the set of functions which are locally in LP(R), i.e., 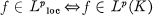 for every compact subset K of R. Cooper showed that
for every compact subset K of R. Cooper showed that 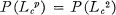 for any p ≧ 2 and that each function in
for any p ≧ 2 and that each function in 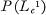 is essentially bounded and hence equal almost everywhere to an ordinary continuous positive definite function in the sense of Bochner.
is essentially bounded and hence equal almost everywhere to an ordinary continuous positive definite function in the sense of Bochner.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1972


