No CrossRef data available.
Article contents
A Counterexample in Lp Approximation by Harmonic Functions
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
For 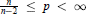 we show that the conditions
we show that the conditions 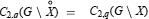 for all open sets G, C2,q denoting Bessel capacity, are not sufficient to characterize the compact sets X with the property that each function harmonic on
for all open sets G, C2,q denoting Bessel capacity, are not sufficient to characterize the compact sets X with the property that each function harmonic on 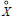 and in Lp(X) is the limit in the Lp norm of a sequence of functions which are harmonic on neighbourhoods of X.
and in Lp(X) is the limit in the Lp norm of a sequence of functions which are harmonic on neighbourhoods of X.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1997
References
[AH]
Adams, D.R., Hedberg, L.I., Function spaces and potential theory, Springer, Berlin and Heidelberg, 1996.Google Scholar
[Ba]
Bagby, T., Approximation in the mean by solutions of elliptic equations, Trans. Amer. Math. Soc.
281(1984), 761–784.Google Scholar
[C]
Carleson, L., Selected problems on exceptional sets, Van Nostrand, Princeton, New Jersey, 1967.Google Scholar
[G]
Gamelin, T.W., Uniform Algebras, Prentice Hall, Englewood Cliff, New Jersey, 1969.Google Scholar
[H1]
Hedberg, L.I., Non-linear potentials and approximation in the mean by analytic functions, Math. Z.
129(1972), 299–319.Google Scholar
[H2]
Hedberg, L.I., Approximation in the mean by solutions of elliptic equations, Duke Math. J.
40(1973), 9–16.Google Scholar
[H3]
Hedberg, L.I., Two approximation problems in function spaces, Ark.Mat.
16(1978), 51–81.Google Scholar
[H4]
Hedberg, L.I., Spectral synthesis in Sobolev spaces, and uniqueness of solutions of the Dirichlet problem, Acta Math.
147(1981), 237–264.Google Scholar
[HW]
Hedberg, L.I. and Wolff, T., Thin sets in nonlinear potential theory, Ann. Inst. Fourier (Grenoble) (4)
33(1983), 161–187.Google Scholar
[MNOV]
Mateu, J., Netrusov, Y., Orobitg, J. and Verdera, J., BMO and Lipschitz approximation by solutions of elliptic equations, Ann. Inst. Fourier (Grenoble) (4)
46(1996), 1057–1081.Google Scholar
[Me]
Meyers, N.G., A theory of capacities for potentials of functions in Lebesgue classes, Math. Scand.
26(1970), 225–292.Google Scholar
[O]
O’Farrell, A.G., Hausdorff content and rational approximation in fractional Lipschitz norms, Trans.Amer. Math. Soc.
228(1977), 187–206.Google Scholar
[P]
Polking, J.C., Approximation in Lp by solutions of elliptic partial differential equations, Amer. J. Math.
94(1972), 1231–1244.Google Scholar
[S]
Stein, E.M., Singular integrals and differentiability properties of functions, Princeton University Press, Princeton, New Jersey, 1970.Google Scholar


