Convergence Factors and Compactness in Weighted Convolution Algebras

Abstract

We study convergence in weighted convolution algebras 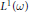${{L}^{1}}\left( \omega \right)$ on 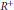${{R}^{+}}$, with the weights chosen such that the corresponding weighted space 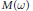$M\left( \omega \right)$ of measures is also a Banach algebra and is the dual space of a natural related space of continuous functions. We determine convergence factor 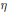$\eta $ for which weak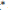$*$-convergence of 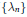$\left\{ {{\text{ }\!\!\lambda\!\!\text{ }}_{n}} \right\}$ to 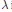$\text{ }\!\!\lambda\!\!\text{ }$ in 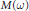$M\left( \omega \right)$ implies norm convergence of 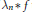${{\text{ }\!\!\lambda\!\!\text{ }}_{n}}*f$ to 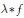$\text{ }\!\!\lambda\!\!\text{ *}f$ in 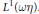${{L}^{1}}\left( \omega \eta \right)$. We find necessary and sufficent conditions which depend on 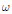$\omega$ and 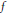$f$ and also find necessary and sufficent conditions for 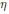$\eta$ to be a convergence factor for all 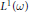${{L}^{1}}\left( \omega \right)$ and all 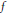$f$ in 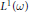${{L}^{1}}\left( \omega \right)$. We also give some applications to the structure of weighted convolution algebras. As a preliminary result we observe that 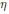$\eta$ is a convergence factor for 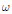$\omega$ and 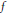$f$ if and only if convolution by 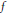$f$ is a compact operator from 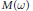$M\left( \omega \right)$ (or 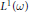${{L}^{1}}\left( \omega \right)$) to 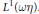${{L}^{1}}\left( \omega \eta \right)$.