Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Touchard, Jacques
1952.
Sur Un Problème De Configurations Et Sur Les Fractions Continues.
Canadian Journal of Mathematics,
Vol. 4,
Issue. ,
p.
2.
Lunnon, W. F.
1968.
A map-folding problem.
Mathematics of Computation,
Vol. 22,
Issue. 101,
p.
193.
Riordan, John
1969.
Memorial note.
Journal of Combinatorial Theory,
Vol. 7,
Issue. 3,
p.
286.
Riordan, John
1975.
The distribution of crossings of chords joining pairs of 2𝑛 points on a circle.
Mathematics of Computation,
Vol. 29,
Issue. 129,
p.
215.
Ismail, Mourad E.H.
Stanton, Dennis
and
Viennot, Gérard
1987.
The Combinatorics of q-Hermite polynomials and the Askey—Wilson Integral.
European Journal of Combinatorics,
Vol. 8,
Issue. 4,
p.
379.
Dulucq, Serge
and
Penaud, Jean-Guy
1993.
Cordes, arbres et permutations.
Discrete Mathematics,
Vol. 117,
Issue. 1-3,
p.
89.
Dale, M.R.T.
and
Moon, J.W.
1993.
The permuted analogues of three Catalan sets.
Journal of Statistical Planning and Inference,
Vol. 34,
Issue. 1,
p.
75.
Penaud, Jean-Guy
1995.
Une preuve bijective d'une formule de Touchard-Riordan.
Discrete Mathematics,
Vol. 139,
Issue. 1-3,
p.
347.
Di Francesco, P.
Golinelli, O.
and
Guitter, E.
1996.
Meanders: a direct enumeration approach.
Nuclear Physics B,
Vol. 482,
Issue. 3,
p.
497.
Di Francesco, P.
Golinelli, O.
and
Guitter, E.
1997.
Meander, folding, and arch statistics.
Mathematical and Computer Modelling,
Vol. 26,
Issue. 8-10,
p.
97.
Francesco, P. Di
Golinelli, O.
and
Guitter, E.
1997.
Meanders and the Temperley-Lieb algebra.
Communications in Mathematical Physics,
Vol. 186,
Issue. 1,
p.
1.
Di Francesco, P.
Golinelli, O.
and
Guitter, E.
1997.
Low-Dimensional Applications of Quantum Field Theory.
Vol. 361,
Issue. ,
p.
87.
Di Francesco, P.
1997.
SU(N) meander determinants.
Journal of Mathematical Physics,
Vol. 38,
Issue. 11,
p.
5905.
Cazals, Frédéric
1997.
Combinatorial Properties of One-Dimensional Arrangements.
Experimental Mathematics,
Vol. 6,
Issue. 1,
p.
87.
Sloane, N. J. A.
1999.
Sequences and their Applications.
p.
103.
Di Francesco, P.
Golinelli, O.
and
Guitter, E.
2000.
Meanders: exact asymptotics.
Nuclear Physics B,
Vol. 570,
Issue. 3,
p.
699.
Di Francesco, P.
2000.
Calogero—Moser— Sutherland Models.
p.
127.
Di Francesco, P.
Guitter, E.
and
Jacobsen, J.L.
2000.
Exact meander asymptotics: a numerical check.
Nuclear Physics B,
Vol. 580,
Issue. 3,
p.
757.
Jensen, Iwan
and
Guttmann, Anthony J
2000.
Critical exponents of plane meanders.
Journal of Physics A: Mathematical and General,
Vol. 33,
Issue. 21,
p.
L187.
Jensen, Iwan
2000.
A transfer matrix approach to the enumeration of plane meanders.
Journal of Physics A: Mathematical and General,
Vol. 33,
Issue. 34,
p.
5953.
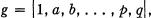 la permutation
la permutation 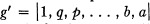 .
.