Article contents
Contractive Representation Theory for the Unitary Group of C(X, M2)
Published online by Cambridge University Press: 20 November 2018
Extract
One motivation for studying representation theory for the unitary group 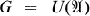 of a unital C*-algebra
of a unital C*-algebra 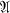 arises from Theoretical Physics. (In the latter connection, Segal [9] and Arveson [1] have developed a representation theory for G. Their approach is in a different direction from ours.) Another motivation for studying the representation theory of G arises out of the desire to unify the theories of amenable von Neumann algebras and amenable locally compact groups.
arises from Theoretical Physics. (In the latter connection, Segal [9] and Arveson [1] have developed a representation theory for G. Their approach is in a different direction from ours.) Another motivation for studying the representation theory of G arises out of the desire to unify the theories of amenable von Neumann algebras and amenable locally compact groups.
A serious problem for such a representation theory is the absence of Haar measure on G in general.
In [7], the author introduced the class RepdG of contractive unitary representations of G, the strong metric condition involved compensating for the lack of Haar measure.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1987
References
- 1
- Cited by


