Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hu, Y.K.
Kopotun, K.A.
and
Yu, X.M.
1999.
Weak Copositive and Intertwining Approximation.
Journal of Approximation Theory,
Vol. 96,
Issue. 2,
p.
213.
Leviatan, D.
2000.
Shape-preserving approximation by polynomials.
Journal of Computational and Applied Mathematics,
Vol. 121,
Issue. 1-2,
p.
73.
Kozlov, Inna
2002.
Interpolation of Cones and Shape-Preserving Approximation.
Journal of Approximation Theory,
Vol. 117,
Issue. 1,
p.
23.
Jianli, Wang
and
Songping, Zhou
2003.
Some converse results on onesided approximation: Justifications.
Analysis in Theory and Applications,
Vol. 19,
Issue. 3,
p.
280.
Smazhenko, I. V.
2005.
Weighted Moduli of Smoothness and Sign-Preserving Approximation.
Ukrainian Mathematical Journal,
Vol. 57,
Issue. 3,
p.
481.
Kopotun, K.A.
Leviatan, D.
and
Shevchuk, I.A.
2021.
Exact order of pointwise estimates for polynomial approximation with Hermite interpolation.
Journal of Approximation Theory,
Vol. 264,
Issue. ,
p.
105538.
Dzyubenko, German
and
Kopotun, Kirill A.
2024.
Onesided, intertwining, positive and copositive polynomial approximation with interpolatory constraints.
Journal of Approximation Theory,
Vol. 299,
Issue. ,
p.
106012.


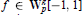 are considered. Both uniform and pointwise estimates, which are exact in some sense, are obtained.
are considered. Both uniform and pointwise estimates, which are exact in some sense, are obtained.