Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-13T06:47:03.238Z Has data issue: false hasContentIssue false
  • English
  • Français

Connected Components of Moduli Stacks of Torsors via Tamagawa Numbers

Published online by Cambridge University Press:  20 November 2018

Kai Behrend  and
Ajneet Dhillon
Kai Behrend
Affiliation:
Department of Mathematics, University of Britich Columbia, Vancouver, BC, V6T 1Z2, [email protected]
Ajneet Dhillon
Affiliation:
Department of Mathematics, Middlesex College, University of Western Ontario, London, ON, N6A 5B7, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 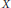$X$ be a smooth projective geometrically connected curve over a finite field with function field 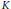$K$. Let 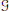$g$ be a connected semisimple group scheme over 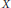$X$. Under certain hypotheses we prove the equality of two numbers associated with 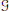$g$. The first is an arithmetic invariant, its Tamagawa number. The second is a geometric invariant, the number of connected components of the moduli stack of 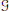$g$-torsors on 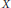$X$. Our results are most useful for studying connected components as much is known about Tamagawa numbers.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 1 , 01 February 2009 , pp. 3 - 28
Copyright
Copyright © Canadian Mathematical Society 2009

References

[AB82] Atiyah, M. and Bott, R., The Yang-Mills equations over Riemann surfaces. Philos. Trans. Roy. Soc. Lond. Ser. A 308 (1982), no. 1505, 523–615.Google Scholar
[AGV72] Artin, M., Grothendieck, A., and Verdier, J. L., eds., Théorie des topos et cohomologie étale des schémas, Tome 2. SGA4, vol. 270 of Lecture Notes in Mathematics, 1972.Google Scholar
[Bal04] Balaji, V., Semistable principal bundles. In: Advances in Algebra and Geometry. Hindustan Book Agency, New Delhi, 2003, pp. 129–145.Google Scholar
[Beh90] Behrend, K., The Lefschetz Trace Formula for theModuli Stack of Principal Bundles. Ph.D. thesis, University of California, Berkeley, 1990.Google Scholar
[Beh93] Behrend, K., The Lefschetz trace formula for algebraic stacks. Invent. Math. 112 (1993), no. 1, 127–149.Google Scholar
[Beh95] Behrend, K., Semi-stability of reductive group schemes over curves. Math. Ann. 301 (1995), no. 2, 281–305.Google Scholar
[Beh03] Behrend, K., Derived ℓ-Adic Categories For Algebraic Stacks. Mem. Amer.Math. Soc. 163 (2003), no. 774, American Mathematical Society, Providence, RI.Google Scholar
[DG70] Demazure, M. and Grothendieck, A., Schemas in Groupes, SGA3. vols. 151, 152, 153 of Lecture Notes inMathematics, Springer-Verlag, New York, Berlin, 1970.Google Scholar
[GR71] Grothendieck, A. and Raynaud, M., Revêtements étales et groupe fondamental. Lecture Notes in Mathematics 224, Springer-Verlag, Berlin, 1971.Google Scholar
[Har69] Harder, G.. Minkowskische Reduktiontheorie über Funktionenkörpern. Invent. Math. 7 (1969), 33–54.Google Scholar
[Har70] Harder, G., Eine bemerkung zu einer arbeit von P. E. Newstead. J. Reine Angew. Math. 242 (1970), 16–25.Google Scholar
[Har74] Harder, G., Chevalley groups over function fields and automorphic forms. Ann. of Math 100 (1974), 249–306.Google Scholar
[Har75] Harder, G., Über die Galoiskohomologie halbenfacher algebraischer Gruppen. III. J. Reine Angew. Math. 274/275 (1975), 125–138.Google Scholar
[HN75] Harder, G. and Narasimhan, M. S., On the cohomology of moduli spaces of vector bundles on curves. Math. Ann. 212 (1975), 212–248.Google Scholar
[Kne67] Kneser, M., Semi-simple algebraic groups. In: Algebraic Number. Theory. Thompson, Washington, D.C. 1967, pp. 250–265.Google Scholar
[Kot88] Kottwitz, R., Tamagawa numbers. Ann. of Math. 127 (1988), no. 3, 629–646.Google Scholar
[Mil80] Milne, J. S., ℓtale Cohomology. Princeton Mathematical Series 33, Princeton University Press, Princeton, NJ, 1980.Google Scholar
[Oes84] Oesterlé, J., Nombre de Tamagawa et groupes unipotents en caractéristique p. Invent. Math. 78 (1984), no. 1, 13–88.Google Scholar
[Ono63] Ono, T., On the Tamagawa number of algebraic tori. Ann. of Math. 78 (1063), 47–73.Google Scholar
[Ono65] Oesterlé, J., On the relative theory of Tamagawa numbers. Ann. of Math. 82 (1965), 88–111.Google Scholar
[Ros00] Rosen, M., Number Theory in Function Fields. Graduate Texts inMathematics 210, Springer-Verlag, New York, 2002.Google Scholar
[Ste68] Steinberg, R., Endomorphisms of linear algebraic groups. Memoirs of the American Mathematical Society 80, American Mathematical Society, Providence, RI, 1968.Google Scholar
[Tel98] Teleman, C., Borel-Weil-Bott theory on the moduli stack of G-bundles over a curve. Invent. Math. 138 (1998), no. 1, 1–57.Google Scholar
[Wei82] Weil, A.. Adeles and Algebraic Groups. Progress in Mathematics 23, Birkhäuser, Boston, MA, 1982.Google Scholar