Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-18T11:23:31.137Z Has data issue: false hasContentIssue false
  • English
  • Français

Cone-Monotone Functions: Differentiability and Continuity

Published online by Cambridge University Press:  20 November 2018

Jonathan M. Borwein  and
Xianfu Wang
Jonathan M. Borwein
Affiliation:
Faculty of Computer Science, Dalhousie University, 6050 University Avenue, Halifax, NS, B3H 1W5, e-mail: [email protected]
Xianfu Wang
Affiliation:
Department of Mathematics and Statistics, Okanagan University College, Kelowna, BC, V1V 1V7, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We provide a porosity-based approach to the differentiability and continuity of real-valued functions on separable Banach spaces, when the function is monotone with respect to an ordering induced by a convex cone 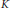$K$ with non-empty interior. We also show that the set of nowhere 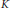$K$-monotone functions has a $\sigma $-porous complement in the space of continuous functions endowed with the uniform metric.

Keywords

Primary: 26B05secondary: 58C20Cone-monotone functionsAronszajn null setdirectionally porous setsGâteaux differentiabilityseparable spaces
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 5 , 01 October 2005 , pp. 961 - 982
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Benyamini, Y. and Lindenstrauss, J., Geometric Nonlinear Functional Analysis. Vol. 1, American Mathematical Society Colloquium Publications 48, American Mathematical Society, Providence, RI, 2000.Google Scholar
[2] Borwein, J. M., Burke, J. V., and Lewis, A. S., Differentiability of cone-monotone functions on separable Banach spaces. Proc. Amer. Math. Soc. 132(2004), 1067–1076.Google Scholar
[3] Borwein, J. M. and Goebel, R., On the nondifferentiability of cone-monotone functions in Banach spaces. CECMPreprint 02:179.Google Scholar
[4] Chabrillac, Y. and Crouzeix, J. P., Continuity and differentiability properties of monotone real functions of several real variables. In: Nonlinear Analysis and Optimization. Math. Programming Stud. 30, North Holland, Amsterdam, 1987, pp. 1–16.Google Scholar
[5] Crouzeix, J. P., A review of continuity and differentiability properties of quasiconvex functions on Rn. In: Convex Analysis and Optimization, (Aubin, J. P., Vinter, R. B., eds.), Research Notes in Mathematics 57, Pitman, Boston, 1982, pp. 18–34.Google Scholar
[6] Preiss, D. and Zajiček, L., Directional derivatives of Lipschitz functions. Isarel J. Math. 125(2001), 1–27.Google Scholar
[7] Preiss, D. and Zajiček, L., Fréchet differentiation of convex functions in a Banach space with a separable dual. Proc. Amer.Math. Soc. 91(1984), 202–204.Google Scholar
[8] Preiss, D., Differentiability of Lipschitz functions on Banach spaces. J. Funct. Anal. 91(1990), 312–345.Google Scholar
[9] Robinov, A. M. and Zaslavski, A., Two porosity results in monotonic analysis. Numer. Funct. Anal. Optim. 23(2002), 651–668.Google Scholar
[10] Saks, S., Theory of the Integral, English translation, Second edition, Stechert, New York, 1937.Google Scholar