Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-11T01:39:14.632Z Has data issue: false hasContentIssue false
  • English
  • Français

Computing Noncommutative Deformations of Presheaves and Sheaves of Modules

Published online by Cambridge University Press:  20 November 2018

Eivind Eriksen
Eivind Eriksen*
Affiliation:
Oslo University College, Postboks 4 St. Olavs Plass, 0130 Oslo, Norway, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We describe a noncommutative deformation theory for presheaves and sheaves of modules that generalizes the commutative deformation theory of these global algebraic structures and the noncommutative deformation theory of modules over algebras due to Laudal.

In the first part of the paper, we describe a noncommutative deformation functor for presheaves of modules on a small category and an obstruction theory for this functor in terms of global Hochschild cohomology. An important feature of this obstruction theory is that it can be computed in concrete terms in many interesting cases.

In the last part of the paper, we describe a noncommutative deformation functor for quasi-coherent sheaves of modules on a ringed space 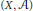$\left( X,\,\mathcal{A} \right)$. We show that for any good 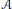$\mathcal{A}$-affine open cover $\cup$ of 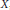$X$, the forgetful functor 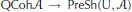$\text{QCoh}\mathcal{A}\,\to \,\text{PreSh}\left( \cup ,\,\mathcal{A} \right)$ induces an isomorphism of noncommutative deformation functors.

Applications. We consider noncommutative deformations of quasi-coherent 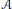$\mathcal{A}$-modules on 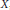$X$ when 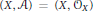$\left( X,\,\mathcal{A} \right)\,=\,\left( X,\,{{\mathcal{O}}_{X}} \right)$ is a scheme or 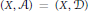$\left( X,\,\mathcal{A} \right)\,=\,\left( X,\,\mathcal{D} \right)$ is a 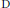$\text{D}$-scheme in the sense of Beilinson and Bernstein. In these cases, we may use any open affine cover of 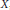$X$ closed under finite intersections to compute noncommutative deformations in concrete terms using presheaf methods. We compute the noncommutative deformations of the left 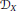${{\mathcal{D}}_{X}}$-module 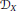${{\mathcal{D}}_{X}}$ when 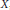$X$ is an elliptic curve as an example.

Keywords

14D1513N10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 3 , 01 June 2010 , pp. 520 - 542
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Beılinson, A. and Bernstein, J., Localisation de g-modules. C. R. Acad. Sci. Paris Sér. I Math. 292(1981), no. 1, 15–18.Google Scholar
[2] Beılinson, A. and Bernstein, J., A proof of Jantzen conjectures. In: I. M. Gel′fand Seminar. Adv. Soviet Math. 16. American Mathematical Society, Providence, RI, 1993, pp. 1–50.Google Scholar
[3] Bourbaki, N., Éléments de mathématique. Fascicule XXVII. Algèbre commutative. Chapitre 1: Modules plats. Chapitre 2: Localisation, Actualités Scientifiques et Industrielles, No. 1290, Herman, Paris, 1961.Google Scholar
[4] Eriksen, E., Iterated extensions in module categories. ar Xiv:math/0406034v1,2004.Google Scholar
[5] Eriksen, E., Computing noncommutative global deformations ofD-modules, ar Xiv:math/0612441v2,2006.Google Scholar
[6] Grothendieck, A., Éléments de géométrie algébrique. I. Le langage des schémas, Inst. Hautes Études Sci. Publ. Math. (1960), no. 4, 228.Google Scholar
[7] Grothendieck, A., Éléments de géométrie algébrique. III. Étude cohomologique des faisceaux cohérents. I. Inst. Hautes Études Sci. Publ. Math. (1961), no. 11, 167.Google Scholar
[8] Grothendieck, A., Fondements de la géométrie algébrique. [Extraits du Séminaire Bourbaki, 1957–1962.]. Secrétariat mathématique, Paris, 1962.Google Scholar
[9] Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV. Inst. Hautes Études Sci. Publ. Math. (1967), no. 32, 361.Google Scholar
[10] Grothendieck, A., Géométrie formelle et géométrie algébrique. Séminaire Bourbaki, Vol. 5, Soc. Math. France, Paris, 1995, pp. Exp. No. 182, 193–220, errata p. 390.Google Scholar
[11] Grothendieck, A., Technique de descente et théorèmes d’existence en géometrie algébrique. I. Généralités. Descente par morphismes fidèlement plats. Séminaire Bourbaki, Vol. 5, Soc. Math. France, Paris, 1995, pp. Exp. No. 190, 299–327.Google Scholar
[12] Hartshorne, R., Algebraic Geometry. Graduate Texts in Mathematics 52, Springer-Verlag, New York, 1977,Google Scholar
[13] Laudal, O. A., Formal Moduli of Algebraic Structures. Lecture Notes in Mathematics 754, Springer, Berlin, 1979.Google Scholar
[14] Laudal, O. A., Matric Massey products and formal moduli. I. In: Algebra, Algebraic Topology and Their Interactions. Lecture Notes in Math. 1183. Springer, Berlin, 1986, pp. 218–240.Google Scholar
[15] Laudal, O. A., Noncommutative deformations of modules. Homology Homotopy Appl. 4(2002), no. 2, part 2, 357–396 (electronic), The Roos Festschrift.Google Scholar
[16] Oort, F., Yoneda extensions in abelian categories. Math. Ann. 153(1964), 227–235. doi:10.1007/BF01360318 Google Scholar
[17] Schlessinger, Michael, Functors of Artin rings. Trans. Amer. Math. Soc. 130(1968), 208–222. doi:10.2307/1994967 Google Scholar
[18] Smith, S. P. and Stafford, J. T., Differential operators on an affine curve. Proc. London Math. Soc. 56(1988), no. 2, 229–259. doi:10.1112/plms/s3-56.2.229 Google Scholar
[19] Van den Bergh, Michel, Differential operators on semi-invariants for tori and weighted projective spaces. In: Topics in Invariant Theory. Lecture Notes in Math. 1478. Springer, Berlin, 1991, pp. 255–272.Google Scholar
[20] Yekutieli, A. and Zhang, J. J., Dualizing complexes and perverse modules over differential algebras. Compos. Math. 141(2005), no. 3, 620–654. doi:10.1112/S0010437X04001307 Google Scholar