Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T05:31:35.408Z Has data issue: false hasContentIssue false
  • English
  • Français

Compound Invariants and Mixed F-, DF-Power Spaces

Published online by Cambridge University Press:  20 November 2018

P. A. Chalov ,
T. Terzioğlu  and
V. P. Zahariuta
P. A. Chalov
Affiliation:
Department of Mechanics and Mathematics, Rostov State University, Rostov-on-Don, Russia, email: [email protected]
T. Terzioğlu
Affiliation:
Sabanci University, Istanbul, Turkey
V. P. Zahariuta*
Affiliation:
Sabanci University, Istanbul, Turkey
*
Current address: Feza Gürsey Institute Çengelköy-Istanbul, Turkey email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The problems on isomorphic classification and quasiequivalence of bases are studied for the class of mixed 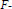$F-$, 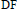$\text{DF}$-power series spaces, i.e. the spaces of the following kind

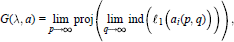$$G(\lambda ,a)=\underset{p\to \infty }{\mathop{\lim }}\,\text{proj}\left( \underset{q\to \infty }{\mathop{\lim }}\,\text{ind}\left( {{\ell }_{1}}\left( {{a}_{i}}\left( p,q \right) \right) \right) \right),$$

where 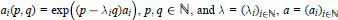${{a}_{i}}(p,\,q)\,=\,\exp \left( \left( p\,-\,{{\lambda }_{i}}q \right){{a}_{i}} \right),\,p,\,q\,\in \,\mathbb{N},\,\text{and}\,\lambda \,\text{=}\,{{\left( {{\lambda }_{i}} \right)}_{i\in \mathbb{N}}},\,a=\,{{({{a}_{i}})}_{i\in \mathbb{N}}}$ are some sequences of positive numbers. These spaces, up to isomorphisms, are basis subspaces of tensor products of power series spaces of 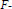$F-$ and 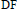$\text{DF}$-types, respectively. The m-rectangle characteristic 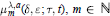$\mu _{m}^{\lambda ,a}\left( \delta ,\,\varepsilon ;\,\tau ,\,t \right),\,m\,\in \,\mathbb{N}$ of the space 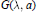$G\left( \text{ }\!\!\lambda\!\!\text{ ,}\,a \right)$ is defined as the number of members of the sequence 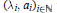${{({{\lambda }_{i}},{{a}_{i}})}_{i\in \mathbb{N}}}$ which are contained in the union of m rectangles 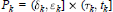${{P}_{k}}\,=\,\left( {{\delta }_{k}},\,{{\varepsilon }_{k}} \right]\,\times \,\left( {{\tau }_{k}},\,{{t}_{k}} \right]$ , 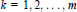$k\,=\,1,2,\ldots ,m$. It is shown that each m-rectangle characteristic is an invariant on the considered class under some proper definition of an equivalency relation. The main tool are new compound invariants, which combine some version of the classical approximative dimensions (Kolmogorov, Pełczynski) with appropriate geometrical and interpolational operations under neighborhoods of the origin (taken from a given basis).

Keywords

46A0446A4546M05
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 6 , 01 December 1998 , pp. 1138 - 1162
Copyright
Copyright © Canadian Mathematical Society 1998

Footnotes

Permanent address: Department of Mechanics and Mathematics Rostov State University Rostov-on-Don Russia

The first author was supported by Tübİtak-Nato Fellowship Program.

References

1. Aytuna, A., Djakov, P.B., Goncharov, A.P., Terzioğlu, T. and Zahariuta, V.P., Some open problems in the theory of locally convex spaces. In: Linear Topological Spaces and Complex Analysis, I, METUTÜBITAK, Ankara, 1994. 147–165.Google Scholar
2. Baran, V.I., Quasiequivalence of absolute bases in Cartesian products of some Köthe spaces. In: Qualitative and approximative methods for operator equations, Yaroslavl 2, 1977. 8–24 (in Russian).Google Scholar
3. Baran, V.I., On quasiequivalence of absolute bases in Cartesian products of Köthe spaces. In: Actual Problems of Mathematical Analysis, Rostov State University, 1978. 13–21 (in Russian).Google Scholar
4. Bergh, J. and Löfström, J., Interpolation spaces. Springer-Verlag, 1976.Google Scholar
5. Bessaga, Cz., Some remarks on Dragilev's theorem. Studia Math. 31(1968), 307–318.Google Scholar
6. Bessaga, Cz., Geometrical methods of the theory of Fréchet spaces. World Scientific, Singapore, New Jersey, Hong Kong, 1986.Google Scholar
7. Bessaga, Cz. and Pełczynski, A., Approximative dimension of linear topological spaces and some its applications. In: Reports of Conference on Functional Analysis, Warsaw, 1960.Google Scholar
8. Bessaga, Cz., A. Pełczynski and S. Rolewicz, Some properties of the space S. Colloq. Math. 7(1959), 45–51.Google Scholar
9. Bessaga, Cz., On diametral approximative dimension and linear homogeneity of F-spaces. Bull. Polish Acad. Sci. 9(1961), 677–683.Google Scholar
10. Chalov, P.A., Triples of Hilbert spaces. Manuscript 1387–81 Dep., deposited at VINITI, 1981.(in Russian).Google Scholar
11. Chalov, P.A., Djakov, P.B., Terzioğlu, T. and Zahariuta, V.P., On Cartesian products of locally convex spaces. In: Linear Topological Spaces and Complex Analysis, II, METU-TÜBITAK, Ankara, 1995. 9–33.Google Scholar
12. Chalov, P.A., Djakov, P.B. and Zahariuta, V.P., Compound invariants and embeddings of Cartesian products. preprint.Google Scholar
13. Chalov, P.A. and Zahariuta, V.P., On linear topological invariants. Manuscript No. 5941-85, deposited at VINITI, 1985.(in Russian).Google Scholar
14. Chalov, P.A., On linear topological invariants on some class of families of Hilbert spaces. Manuscript No.3862-B 86, deposited at VINITI, 1986.(in Russian).Google Scholar
15. Chalov, P.A., On uniqueness of unconditional basis in families of Banach spaces. Preprint Series in Pure and Applied Math. 26, Marmara Research Center, 1995.Google Scholar
16. Chalov, P.A., On quasi-diagonal isomorphisms of generalized power spaces. In: Linear Topological Spaces and Complex Analysis, II, METU-TÜBITAK, Ankara, 1995. 35–44.Google Scholar
17. Crone, L. and Robinson, W.. Every nuclear Fréchet space with a regular basis has the quasi-equivalence property. Studia Math. 52(1974), 203–207.Google Scholar
18. Djakov, P.B., A short proof of the theorem on quasi-equivalence of regular bases. StudiaMath. 55(1975), 269–271.Google Scholar
19. Djakov, P.B., Yurdakul, M. and Zahariuta, V.P., On Cartesian products of Köthe spaces. Bull. Polish Acad. Sci. Math. 43(1995), 113–117.Google Scholar
20. Djakov, P.B., Isomorphic classification of Cartesian products of power series spaces. Michigan Math. J. 43(1996), 221–229.Google Scholar
21. Djakov, P.B. and Zahariuta, V.P., On Dragilev-type power Köthe spaces. Studia Math. 120(1996), 219–234.Google Scholar
22. Dragilev, M.M., The canonical form of a basis in a space of analytic functions. Uspekhi Mat. Nauk 15(1960), 181–188.(in Russian).Google Scholar
23. Dragilev, M.M., On regular bases in nuclear spaces. Mat. Sb. 68(1965), 153–173.(in Russian).Google Scholar
24. Dragilev, M.M., Bases in Köthe spaces. Rostov State University, Rostov-on-Don, 1983.(in Russian).Google Scholar
25. Dubinsky, E., The structure of nuclear Fréchet spaces. Lecture Notes in Math. 720, 1979.Google Scholar
26. Goncharov, A., Terzioğlu, T. and Zahariuta, V.,On isomorphic classification of spacesŝ E0 1(a). In: Linear Topological Spaces and Complex Analysis, I, METU-TÜBITAK, Ankara, 1994. 14–24.Google Scholar
27. Goncharov, A., On isomorphic classification of tensor products E1(a)Ê0 1(b). Dissertationes Math., CCCL, Warszawa, 1996. 1–27.Google Scholar
28. Goncharov, A.P. and Zahariuta, V.P., Linear topological invariants for tensor products of power F- and DF-spaces. Turkish J. Math. 19(1995), 90–101.Google Scholar
29. Grothendieck, A., Produits tensoriels topologiques et espaces nucléaires. Mem. Amer. Math. Soc. 16(1955).Google Scholar
30. Kocatepe, M. and Zahariuta, V., Köthe spaces modeled on spaces ofC1 functions. StudiaMath. 121(1996), 1–14.Google Scholar
31. Kolmogorov, A.N., On the linear dimension of vector topological spaces. Dokl. Acad. Nauk SSSR 120(1958), 239–241.(in Russian).Google Scholar
32. Kondakov, V.P., On quasi-equivalence of regular bases in Köthe spaces. Mat. Anal. i ego prilozheniya, Rostov State University, Rostov-on-Don 5, 1974. 210–213 (in Russian).Google Scholar
33. Kondakov, V.P., Problems of geometry of non-normable spaces. Rostov State University, Rostov-on-Don, 1983.(in Russian).Google Scholar
34. Krein, S.G., Petunin, Yu. I. and Semenov, E.M., Interpolation of linear operators. Nauka, Moscow, 1978.(in Russian).Google Scholar
35. Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces. Springer-Verlag, Berlin, Heidelberg, New York, 1977.Google Scholar
36. Mityagin, B.S., Approximative dimension and bases in nuclear spaces. RussianMath. Surveys 16(1961), 59–127.Google Scholar
37. Mityagin, B.S., Nuclear Riesz scales. Dokl. Akad. Nauk SSSR 137(1961), 519–522.(in Russian).Google Scholar
38. Mityagin, B.S. , Sur l’equivalence des bases unconditional dans les echelles de Hilbert. C. R. Acad. Sci. Paris 269(1969), 426–428.Google Scholar
39. Mityagin, B.S., Equivalence of bases in Hilbert scales. Studia Math. 37(1970), 111–137.(in Russian).Google Scholar
40. Mityagin, B.S., Non-Schwartzian power series spaces. Math. Z. 182(1983), 303–310.Google Scholar
41. Peetre, J., On interpolation functions. Acta Sci. Math. 27(1966), 167–171. II, ibid. 29(1968), 91–92. III ibid. 30(1969), 235–239.Google Scholar
42. Pełczynski, A., On the approximation of S-spaces by finite-dimensional spaces. Bull. Polish Acad. Sci. 5(1957), 879–881.Google Scholar
43. Rolewicz, S., On spaces of holomorphic functions. Studia Math. 21(1962), 135–160.Google Scholar
44. Mityagin, B.S., Metric linear Spaces. Polish Scientific Publishers, Warsaw, 1984.Google Scholar
45. Terzioğlu, T., Smooth sequence spaces. In: Proceedings of Symp. on Funct. Anal., Silivri, 1974. 31–41.Google Scholar
46. Mityagin, B.S., Unstable Köthe spaces and the functor Ext. Tr. J.Math. 10(1986), 227–231.Google Scholar
47. Mityagin, B.S., Some invariants of Fréchet spaces and imbeddings of smooth sequence spaces. Advances in the Theory of Fréchet Spaces, Kluwer Academic Publishers, Dordrecht-Boston-London, 1988. 305–324.Google Scholar
48. Tikhomirov, V.M., Some problems of approximation theory. Moscow University, Moscow, 1976.(in Russian).Google Scholar
49. Vogt, D., Charakterisierung der Unterräume von s. Math. Z. 155(1977), 109–117.Google Scholar
50. Vogt, D., Eine Charakterisierung der Potenzreihenräume von endlichem Typ und ihre Folgerungen. Manuscripta Math. 37(1982), 269–301.Google Scholar
51. Vogt, D., Frécheträume, zwischen denen jede stetige lineare Abdildung beschränkt ist. J. Reine. Angew. Math. 345(1983), 182–200.Google Scholar
52. Vogt, D., Power series spaces representations of nuclear Fréchet spaces. Trans. Amer. Math. Soc. 319(1990), 191–208.Google Scholar
53. Wagner, M.J., Quotienträume von stabilen Potenzreihenräumen unendlichen Typs. Manuscripta Math. 31(1980), 97–109.Google Scholar
54. Yurdakul, M. and Zahariuta, V.P., Linear topological invariants and isomorphic classification of Cartesian products of locally convex spaces. Tr. J.Math. 19(1995), 37–47.Google Scholar
55. Zahariuta, V.P., On isomorphisms of Cartesian products of linear topological spaces. Funk. Anal. i ego Pril. 4(1970), 87–88.(in Russian).Google Scholar
56. Zahariuta, V.P., Linear topological invariants and isomorphisms of spaces of analytic functions. Matem. analiz i ego pril. 2, Rostov Univ., Rostov-on-Don, 1970. 3–13; ibid. 3, 1971. 176–180 (in Russian).Google Scholar
57. Zahariuta, V.P., On the isomorphism of Cartesian products of locally convex spaces. Studia Math. 46(1973), 201–221.Google Scholar
58. Zahariuta, V.P., Some linear topological invariants and isomorphisms of tensor products of scale's centers. Izv. Severo-Kavkaz. Nauchn. Tsentra Vyssh. Shkoly Tekhn. Nauk 4(1974), 62–64.(in Russian).Google Scholar
59. Zahariuta, V.P., On isomorphisms and quasi-equivalence of bases of power Köthe spaces. Soviet Math. Dokl. 16(1975), 411–414.Google Scholar
60. Zahariuta, V.P., On isomorphisms and quasi-equivalence of bases of power Köthe spaces. In: Proceedings of 7th winter school in Drogobych, CEMI, Moscow, 1976. 101–126 (in Russian).Google Scholar
61. Zahariuta, V.P., Generalized Mityagin's invariants and continuum pairwise nonisomorphic spaces of analytic functions. Funktsional Anal. i Prilozhen 11(1977), 24–30.(in Russian).Google Scholar
62. Zahariuta, V.P., Synthetic diameters and linear topological invariants. School on Operator Theory in Function Spaces, abstracts of reports, Minsk, 1978. 51–52 (in Russian).Google Scholar
63. Zahariuta, V.P., Compact operators and isomorphisms of Köthe spaces. In: Actual Problems of Mathematical Analysis,Rostov State University, Rostov-on-Don, 1978. 62–71 (in Russian).Google Scholar
64. Zahariuta, V.P., Linear topological invariants and their application to generalized power spaces. Rostov State University, 1979.(in Russian).Google Scholar
65. Zahariuta, V.P., Isomorphisms of spaces of analytic functions. Soviet Math. Dokl. 22(1980), 631–634.Google Scholar
66. Zahariuta, V.P., Linear topological invariants and their application to isomorphic classification of generalized power spaces. Turkish J. Math. 20(1996), 237–289.Google Scholar