Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-18T09:44:32.505Z Has data issue: false hasContentIssue false
  • English
  • Français

A Compositional Shuffle Conjecture Specifying Touch Points of the Dyck Path

Published online by Cambridge University Press:  20 November 2018

J. Haglund ,
J. Morse  and
M. Zabrocki
J. Haglund
Affiliation:
Department of Mathematics, University of Pennsylvania, Philadelphia, PA 19104-6395, USA email: [email protected]
J. Morse
Affiliation:
Department of Mathematics, Drexel University, Philadelphia, PA 19104, USA email: [email protected]
M. Zabrocki
Affiliation:
Department of Mathematics and Statistics, York University, Toronto, ON M3J 1P3 email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

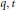We introduce a $q,\,t$-enumeration of Dyck paths that are forced to touch the main diagonal at specific points and forbidden to touch elsewhere and conjecture that it describes the action of the Macdonald theory 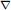$\nabla $ operator applied to a Hall–Littlewood polynomial. Our conjecture refines several earlier conjectures concerning the space of diagonal harmonics including the “shuffle conjecture” (Duke J. Math. 126 (2005), pp. 195 − 232) for 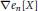$\nabla {{e}_{n}}\left[ X \right]$. We bring to light that certain generalized Hall–Littlewood polynomials indexed by compositions are the building blocks for the algebraic combinatorial theory of 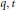$q,\,t$-Catalan sequences, and we prove a number of identities involving these functions.

Keywords

05E0533D52Dyck PathsParking functionsHall–Littlewood symmetric functions
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 4 , 01 August 2012 , pp. 822 - 844
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Bergeron, N., Descouens, F., and Zabrocki, M., A filtration of (q, t)-Catalan numbers. Adv. in Appl. Math. 44(2010), no. 1, 16–36. http://dx.doi.org/10.1016/j.aam.2009.03.002 Google Scholar
[2] Bergeron, F., Garsia, A. M., Haiman, M., and Tesler, G., Identities and positivity conjectures for some remarkable operators in the theory of symmetric functions. Methods Appl. Anal. 6(1999), no. 3, 363–420.Google Scholar
[3] Garsia, A. M. and Haglund, J., A positivity result in the theory of Macdonald polynomials. Proc. Natl. Acad. Sci. USA 98(2001), no. 8, 4313–4316. http://dx.doi.org/10.1073/pnas.071043398 Google Scholar
[4] Garsia, A. M. and Haglund, J., A proof of the q, t-Catalan positivity conjecture. La CIM 2000 Conference on Combinatorics, Computer Science and Applications (Montreal, QC). Discrete Math. 256(2002), no. 3, 677–717. http://dx.doi.org/10.1016/S0012-365X(02)00343-6 Google Scholar
[5] Garsia, A. M., Xin, G., and Zabrocki, M., Hall-Littlewood operators in the theory of parking functions and diagonal harmonics. Int. Math. Res. Notices (2011), published online April 29, 2011. http://dx.doi.org/10.1093/imrn/rnr060 Google Scholar
[6] Haglund, J., Conjectured statistics for the q, t-Catalan numbers. Adv. Math. 175(2003), no. 2, 319–334. http://dx.doi.org/10.1016/S0001-8708(02)00061-0 Google Scholar
[7] Haglund, J., A proof of the q, t-Schröder conjecture. Int. Math. Res. Notices 11(2004), no. 11, 525–560.Google Scholar
[8] Haglund, J., The q, t-Catalan numbers and the space of diagonal harmonics. University Lecture Series, 41, American Mathematical Society, Providence, RI, 2008.Google Scholar
[9] Haglund, J., Haiman, M., Loehr, N., Remmel, J. B., and Ulyanov, A., A combinatorial formula for the character of the diagonal coinvariants. Duke Math. J. 126(2005), no. 2, 195–232. http://dx.doi.org/10.1215/S0012-7094-04-12621-1 Google Scholar
[10] Haiman, M., Hilbert schemes, polygraphs, and the Macdonald positivity conjecture. J. Amer. Math. Soc. 14(2001), no. 4, 941–1006. http://dx.doi.org/10.1090/S0894-0347-01-00373-3 Google Scholar
[11] Haiman, M., Vanishing theorems and character formulas for the Hilbert scheme of points in the plane. Invent. Math. 149(2002), no. 2, 371–407. http://dx.doi.org/10.1007/s002220200219 Google Scholar
[12] Jing, N. H., Vertex operators and Hall-Littlewood symmetric functions. Adv. Math. 87(1991), no. 2, 226–248. http://dx.doi.org/10.1016/0001-8708(91)90072-F Google Scholar
[13] Lam, T., Schubert polynomials for the affine Grassmannian. J. Amer. Math Soc 21(2008), no. 1, 259–281.Google Scholar
[14] Lapointe, L., Lascoux, A., and Morse, J., Tableau atoms and a new Macdonald positivity conjecture. Duke Math. J. 116(2003), no. 1, 103–146. http://dx.doi.org/10.1215/S0012-7094-03-11614-2 Google Scholar
[15] Lapointe, L. and Morse, J., Schur function analogs for a filtration of the symmetric function space. J. Combin. Theory Ser. A 101(2003), no. 2, 191–224. http://dx.doi.org/10.1016/S0097-3165(02)00012-2 Google Scholar
[16] Lapointe, L. and Morse, J., A k-tableaux characterization of k-Schur functions. Adv Math 213(2007), no. 1, 183–204. http://dx.doi.org/10.1016/j.aim.2006.12.005 Google Scholar
[17] Lapointe, L. and Morse, J., Quantum cohomology and the k-Schur basis. Trans. Amer. Math. Soc. 360(2008), no. 4, 2021–2040. http://dx.doi.org/10.1090/S0002-9947-07-04287-0 Google Scholar
[18] Loehr, N. and G. S.Warrington, Nested quantum Dyck paths and r(s_). Int. Math. Res. Not. IMRN 2008, no. 5, Art. ID rnm 157, 29 pp.Google Scholar
[19] Macdonald, I. G., Symmetric functions and Hall polynomials. Second ed. Oxford Mathematical Monographs, Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 1995.Google Scholar