Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T22:03:56.006Z Has data issue: false hasContentIssue false
  • English
  • Français

Composition operators on μ-Bloch spaces

Part of: Special classes of linear operators Linear function spaces and their duals Holomorphic functions of several complex variables

Published online by Cambridge University Press:  20 November 2018

Huaihui Chen  and
Paul Gauthier
Huaihui Chen
Affiliation:
Department of Mathematics, Nanjing Normal University, Nanjing 210097, P.R.China, [email protected]
Paul Gauthier
Affiliation:
Mathématiques et statistique, Université de Montréal, CP-6128 Centre Ville, Montréal, QC, H3C 3J7, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

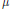Given a positive continuous function $\mu $ on the interval 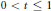$0\,<\,t\,\le \,1$, we consider the space of so-called 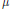$\mu $-Bloch functions on the unit ball. If 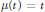$\mu \left( t \right)\,=\,t$, these are the classical Bloch functions. For 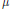$\mu $, we define a metric 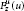$F_{z}^{\mu }\left( u \right)$ in terms of which we give a characterization of 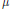$\mu $-Bloch functions. Then, necessary and sufficient conditions are obtained in order that a composition operator be a bounded or compact operator between these generalized Bloch spaces. Our results extend those of Zhang and Xiao.

MSC classification

Primary: 47B33: Composition operators
Secondary: 32A18: Bloch functions, normal functions 32A70: Functional analysis techniques 46E15: Banach spaces of continuous, differentiable or analytic functions
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 1 , 01 February 2009 , pp. 50 - 75
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Anderson, J. M., Clunie, J. and Ch. Pommerenke, On Bloch functions and normal functions, J. Reine Angew. Math. 240 (1974), 12–37.Google Scholar
[2] Ahlfors, L. V., Conformal Invariants: topics in geometric function theory. McGraw-Hill, New York, 1973.Google Scholar
[3] Hu, Z., Composition operators between Bloch-type spaces in the polydisc, Sci. China, Ser. A 48 (Supp)(2005), 268–282.Google Scholar
[4] Madigan, K. and Matheson, A., Compact composition operators on the Bloch space, Trans. Amer. Math. Soc. 437 (1995), no. 7, 2679–2687.Google Scholar
[5] Rudin, W., Function Theory in the Unit Ball of Cn. Springer-Verlag, New York-Heidelberg-Berlin, 1980, pp. 23–30.Google Scholar
[6] Ohno, S., Stroethoff, K. and Zhao, R., Weighted composition operators between Bloch-type spaces, Rocky Mountain J. Math. 33 (2003), no. 1, 191–215.Google Scholar
[7] Shi, J. and Luo, L., Composition operators on the Bloch space of several complex variables. Acta Math. Sin.(Engl. Ser.) 16 (2000), no. 1, 85–98.Google Scholar
[8] Timoney, R., Bloch functions in several complex variables I. Bull. London Math. Soc. 12 (1980), no. 4, 241–267.Google Scholar
[9] Timoney, R., Bloch functions in several complex variables II. J. Reine Angew. Math. 319 (1980), 1–22.Google Scholar
[10] Tsuji, M., Potential Theory in Modern Function Theory. Maruzen Co., Ltd., Tokyo, 1959, pp. 259–260.Google Scholar
[11] Yang, W. and Ouyang, C., Exact location of α-Bloch spaces in Lpα and Hp of a complex unit ball, Rocky Mountain J. Math. 30 (2000), no. 3, 1151–1169.Google Scholar
[12] Zhang, X. and Xiao, J., Weighted composition operators between μ-Bloch spaces on the unit ball. Sci.China Ser. A 48 (2005), no. 10, 1349–1368.Google Scholar
[13] Zhou, Z. and Shi, J., Compact composition operators on the Bloch space of polydiscs, Science in China, Series A, 31 (2001), 111–116.Google Scholar
[14] Zhu, K., Bloch type spaces of analytic functions. RockyMountain J. Math. 23 (1993), no. 3, 1143–1177.Google Scholar
[15] Zhu, K., Spaces of holomorphic functions in the unit ball. Graduate Texts in Mathematics, 226, Springer-Verlag, New York, 2005.Google Scholar