Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-02T20:41:31.129Z Has data issue: false hasContentIssue false
  • English
  • Français

Completely Reducible Operator Algebras and Spectral Synthesis

Published online by Cambridge University Press:  20 November 2018

Shlomo Rosenoer
Shlomo Rosenoer*
Affiliation:
Bol'shaya Serpuhovskaya ul., 31, korp. 6, app. 229A, Moscow, U.S.S.R.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An algebra 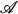of bounded operators on a Hilbert space H is said to be reductive if it is unital, weakly closed and has the property that if M ⊂ H is a (closed) subspace invariant for every operator in 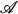, then so is M⊥. Loginov and Šul'man [6] and Rosenthal [9] proved that if 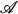is an abelian reductive algebra which commutes with a compact operator K having a dense range, then 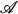is a von Neumann algebra. Note that in this case every invariant subspace of 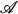is spanned by one-dimensional invariant subspaces. Indeed, the operator KK* commutes with 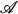. Hence its eigenspaces are invariant for 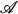, so that H is an orthogonal sum of the finite-dimensional invariant subspaces of 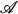From this our claim easily follows.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 5 , 01 October 1982 , pp. 1025 - 1035
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. T., Ando., A note on invariant subspaces of a compact normal operator, Arch. Math. 14 (1963), 337–340./Google Scholar
2. Bochner, S. and J., von Neumann, Almost periodic functions in a group, II, Trans. Amer. Math. Soc. 37 (1935), 21–50./Google Scholar
3. Dunford, N. and Schwartz, J. T., Linear operators, Part III: Spectral operators (Interscience, New York, 1971./Google Scholar
4. C.-K., Fong, Operator algebras with complemented invariant subspace lattices, Indiana Univ. Math. J. 26 (1977), 1045–1056./Google Scholar
5. Gillespie, T. A., Boolean algebras of projections and reflexive algebras of operators, Proc. London Math. Soc. 37 (1978), 56–74./Google Scholar
6. Loginov, A. I. and V. S., Sul'man, On reductive operators and operator algebras, Izv. AN SSSR, Ser. Math 40 (1976), 845–854 (Russian)./Google Scholar
7. Lomonosov, V. J., Invariant subspaces for the family of operators which commute with a completely continuous operator, Funct. Anal, and Appl. 7 (1973), 213–214./Google Scholar
8. Nordgren, E. A., Radjavi, H. and Rosenthal, P., On operators with reducing invariant subspaces, Amer. J. Math. 97 (1975), 559–570./Google Scholar
9. Rosenthal, P., On commutants of reductive operator algebras, Duke Math. J. 41 (1974), 829–834./Google Scholar
10. Sarason, D. E., Invariant subspaces and unstarred operator algebras, Pacific J. Math. 17 (1966), 511–517./Google Scholar