Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-04T20:09:16.318Z Has data issue: false hasContentIssue false
  • English
  • Français

The Complete (Lp, Lp) Mapping Properties of Some Oscillatory Integrals in Several Dimensions

Published online by Cambridge University Press:  20 November 2018

G. Sampson  and
P. Szeptycki
G. Sampson
Affiliation:
Department of Mathematics, Auburn University, Auburn, Albama 36849-5310, U.S.A.
P. Szeptycki
Affiliation:
Department of Mathematics, University of Kansas, Lawrence, Kansas 66045-2142, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that the operators 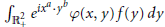$\int{_{\mathbb{R}_{+}^{2}}{{e}^{i{{x}^{a}}\cdot {{y}^{b}}}}\varphi (x,y)f(y)dy}$ map 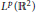${{L}^{p}}({{\mathbb{R}}^{2}})$ into itself for 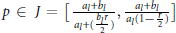$p\,\in \,J\,=\,\,\left[ \frac{{{a}_{1}}+{{b}_{1}}}{{{a}_{1}}+(\frac{{{b}_{1}}r}{2})},\frac{{{a}_{1}}+{{b}_{1}}}{{{a}_{1}}+(1-\frac{r}{2})} \right]$ if 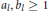${{a}_{l}},{{b}_{l}}\ge 1$ and 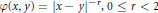$\varphi (x,y)=|x-y{{|}^{-r}},0\le r<2$ , the result is sharp. Generalizations to dimensions 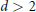$d\,>\,2$ are indicated.

Keywords

42B2046B7047G10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 5 , 01 October 2001 , pp. 1031 - 1056
Copyright
Copyright © Canadian Mathematical Society 2001

References

[CP] Cheng, L. C. and Pan, Y., Lp Estimates For Oscillatory Integral Operators. Proc. Amer. Math. Soc. (10) 127(1999), 2995–3002.Google Scholar
[JS] Jurkat, W. B. and Sampson, G., The complete solution to the (Lp, Lq ) mapping problem for a class of oscillating kernels. Indiana Univ. Math. J. 30(1981), 403–413.Google Scholar
[P1] Pan, Y., Uniform estimates for oscillatory integral operators. J. Funct. Anal. 100(1991), 207–220.Google Scholar
[P2] Pan, Y., Hardy spaces and oscillatory singular integrals. Rev.Mat. Ibero 7(1991), 55–64.Google Scholar
[PSS] Pan, Y., Sampson, G. and Szeptycki, P., L 2 and Lp estimates for oscillatory integrals and their extended domains. Studia Math. (3) 122(1997), 201–224.Google Scholar
[PS] Pan, Y. and Sampson, G., The complete (Lp, Lp ) mapping properties for a class of oscillatory integrals. J. Fourier Anal. Appl. (1) 4(1998), 93–103.Google Scholar
[PhS1] Phong, D. H. and Stein, E. M., Hilbert integrals, singular integrals and Radon transforms I. Acta Math. 157(1986), 99–157.Google Scholar
[PhS2] Phong, D. H. and Stein, E. M., Oscillatory integrals with polynomial phases. Invent. Math. 110(1992), 39–62.Google Scholar
[RS] Ricci, F. and Stein, E. M., Harmonic analysis on nilpotent groups and singular integrals I. J. Funct. Anal. 73(1987), 179–184.Google Scholar
[S] Sampson, G., L 2 Estimates for oscillatory integrals. Colloq. Math. (2) 76(1998), 201–211.Google Scholar
[SS] Sampson, G. and Szeptycki, P., Estimates of oscillatory integrals. preprint.Google Scholar
[St] Stein, E. M., Harmonic Analysis: Real-Variable Methods, Othogonality and Oscillatory Integrals. Princeton Univ. Press, Princeton, N.J., 1993.Google Scholar