No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Let R be a ring with involution *. We denote by S, K and Z = Z(R) the symmetric, the skew and the central elements of R respectively.
In [4] Herstein defined the hypercenter T(R) of a ring R as
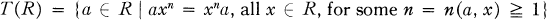
and he proved that in case R is without non-zero nil ideals then T(R) = Z(R).
In this paper we offer a partial extension of this result to rings with involution.
We focus our attention on the following subring of R:

(We shall write H(R) as H whenever there is no confusion as to the ring in question.)
Clearly H contains the central elements of R. Our aim is to show that in a semiprime ring R with involution which is 2 and 3-torsion free, the symmetric elements of H are central.