Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T23:53:11.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Combinatorics of the geometry of Wilson loop diagrams I: equivalence classes via matroids and polytopes

Part of: Quantum field theory; related classical field theories

Published online by Cambridge University Press:  26 February 2021

Susama Agarwala ,
Siân Fryer  and
Karen Yeats
Susama Agarwala*
Affiliation:
Johns Hopkins Applied Physics Lab, Laurel, MD, USA
Siân Fryer
Affiliation:
UC Santa Barbara, Santa Barbara, CA93106, USA e-mail: [email protected]
Karen Yeats
Affiliation:
Combinatorics and Optimization, University of Waterloo, Waterloo, ON, Canada e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Wilson loop diagrams are an important tool in studying scattering amplitudes of SYM 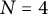$N=4$ theory and are known by previous work to be associated to positroids. We characterize the conditions under which two Wilson loop diagrams give the same positroid, prove that an important subclass of subdiagrams (exact subdiagrams) corresponds to uniform matroids, and enumerate the number of different Wilson loop diagrams that correspond to each positroid cell. We also give a correspondence between those positroids which can arise from Wilson loop diagrams and directions in associahedra.

Keywords

Wilson loop diagramsNkMHV diagramspositroidsN = 4 SYM theory

MSC classification

Primary: 81T60: Supersymmetric field theories
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 4 , August 2022 , pp. 1177 - 1208
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

SA was partially supported by an Office of Naval Research grant. KY is supported by an NSERC Discovery grant, by the Canada Research Chair program, and also, over some of the time this work was developed, by a Humboldt Fellowship from the Alexander von Humboldt foundation.

References

Adamo, T., Bullimore, M., Mason, L., and Skinner, D., Scattering amplitudes and Wilson loops in twistor space . J. Phys. A 44(2011), no. 45, 454008, 48. arXiv:1104.2890 CrossRefGoogle Scholar
Agarwala, S. and Fryer, S., A study in ${\mathsf{Gr}}_{\ge 0}\left(2,6\right)$ : from the geometric case book of Wilson loop diagrams and SYM $N=4$ . Preprint, 2018. arXiv:1803.00958 Google Scholar
Agarwala, S., Fryer, S., and Yeats, K., Combinatorics of the geometry of Wilson loop diagrams II: Grassmann necklaces, dimensions, and denominators. Preprint, 2019. arXiv:1910.12158.Google Scholar
Agarwala, S. and Marcott, C., Wilson loops in SYM $N=4$ do not parametrize an orientable space. Preprint, 2018. arXiv:1807.05397 Google Scholar
Agarwala, S. and Marin-Amat, E., Wilson loop diagrams and positroids . Commun. Math. Phys. 350(2017), no. 2, 569–601. arXiv:1509.06150 CrossRefGoogle Scholar
Arkani-Hamed, N., Bourjaily, J. L., Cachazo, F., Goncharov, A. B., Postnikov, A., and Trnka, J., Scattering amplitudes and the positive Grassmannian. Preprint, 2012. arXiv:1212.5605 CrossRefGoogle Scholar
Arkani-Hamed, N. and Trnka, J., Into the amplituhedron . J. High Energy Phys. 12(2014), 182. arXiv:1312.7878 CrossRefGoogle Scholar
Arkani-Hamed, N. and Trnka, J., The amplituhedron . J. High Energy Phys. 10(2014), 030. arXiv:1312.2007 CrossRefGoogle Scholar
Britto, R., Cachazo, F., Feng, B., and Witten, E., Direct proof of the tree-level scattering amplitude recursion relation in Yang-Mills theory . Phys. Rev. Lett. 94(2005), no. 18, 181602, 4. arXiv:hep-th/0501052 CrossRefGoogle ScholarPubMed
Cachazo, F., Svrcek, P., and Witten, E., MHV vertices and tree amplitudes in gauge theory . J. High Energy Phys. 21(2004), no. 9, 006. arXiv:hep-th/0403047 CrossRefGoogle Scholar
Ceballos, C., Santos, F., and Ziegler, G. M., Many non-equivalent realizations of the associahedron . Combinatorica 35(2015), no. 5, 513–551. arXiv:1109.5544 CrossRefGoogle Scholar
Chavez, A. and Gotti, F., Dyck paths and positroids from unit interval orders . J. Combin. Theory Ser. A 154(2018), 507–532. arXiv:1611.09279 CrossRefGoogle Scholar
Eden, B., Heslop, P., and Mason, L., The correlahedron . J. High Energy Phys. 2017(2017), no. 9, 156, front matter+40, arXiv:1701.00453 CrossRefGoogle Scholar
Galashin, P. and Lam, T., Parity duality for the amplituhedron. Preprint, 2020. arXiv:1805.00600 CrossRefGoogle Scholar
Heslop, P. and Stewart, A., The twistor Wilson loop and the Amplituhedron . J. High Energy Phys. 2018(2018), no. 10, 142, front matter+18, arXiv:1807.05921 CrossRefGoogle Scholar
Karp, S. N., Williams, L., and Zhang, Y. X., Decompostions of amplituhedra. Preprint, 2017. arXiv:1708.09525.Google Scholar
Laskar, R., Mulder, H. M., and Novick, B., Maximal outerplanar graphs as chordal graphs, path-neighborhood graphs, and triangle graphs . Australas. J. Combin. 52(2012), 185–195.Google Scholar
Marcott, C., Basis shape loci and the positive Grassmannian. Preprint, 2019. arXiv:1904.13361 Google Scholar
Mitchell, S., Algorithms on trees and maximal outerplanar graphs: design, complexity analysis and data structures study. Ph.D. thesis, University of Virginia, 1977.Google Scholar
Oxley, J., Matroid theory. Oxford Graduate Texts in Mathematics, 21, 2nd ed., Oxford University Press, Oxford, UK, 2011.Google Scholar
Postnikov, A., Total positivity, Grassmannians, and networks. Preprint, 2006.arXiv:math/0609764 Google Scholar
Przytycki, J. H. and Sikora, A. S., Polygon dissections and Euler, Fuss, Kirkman, and Cayley numbers . J. Combin. Theory Ser. A 92(2000), no. 1, 68–76. arXiv:math/9811086 CrossRefGoogle Scholar
Stanley, R. P., Enumerative combinatorics . Vol. 2, Cambridge Studies in Advanced Mathematics, 62, Cambridge University Press, Cambridge, MA, 1999. With a foreword by Gian-Carlo Rota and appendix 1 by Sergey Fomin.CrossRefGoogle Scholar
Ziegler, G. M., Lectures on polytopes. Vol. 152, Graduate Texts in Mathematics, Springer-Verlag, New York, NY, 1995.CrossRefGoogle Scholar