Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-08T05:32:21.418Z Has data issue: false hasContentIssue false
  • English
  • Français

Combinatorial Problems

Published online by Cambridge University Press:  20 November 2018

S. Chowla  and
H. J. Ryser
S. Chowla
Affiliation:
University of Kansas, Ohio State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

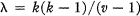Let it be required to arrange v elements into v sets such that every set contains exactly k distinct elements and such that every pair of sets has exactly elements in common 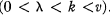. This combinatorial problem is studied in conjunction with several similar problems, and these problems are proved impossible for an infinitude of v and k. An incidence matrix is associated with each of the combinatorial problems, and the problems are then studied almost entirely in terms of their incidence matrices. The techniques used are similar to those developed by Bruck and Ryser for finite projective planes [3]. The results obtained are of significance in the study of Hadamard matrices [6;8], finite projective planes [9], symmetrical balanced incomplete block designs [2; 5], and difference sets [7].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 2 , 1950 , pp. 93 - 99
Copyright
Copyright © Canadian Mathematical Society 1950

References

[1] Bachmann, ,Paul, Die Lehre von der Kreistheilung (Leipzig, 1872), 204.Google Scholar
[2] Bose, R. C , “On the Construction of Balanced Incomplete Block Designs,” Annals of Eugenics, vol. 9 (1939), 353–399.Google Scholar
[3] Bruck, R. H. and Ryser, H. J., “The Nonexistence of Certain Finite Projective Planes,” Can. J. Math., vol. 1 (1949), 88–93.Google Scholar
[4] Hall, ,Marshall, , “Cyclic Projective Planes,” Duke Math. J. (1947), 1079–1090.Google Scholar
[5] Levi, F. W., Finite Geometrical Systems (University of Calcutta, 1942).Google Scholar
[6] Paley, R. E. A. C., “On Orthogonal Matrices,” J . of Math, and Physics, vol. 12 (1933),311–320.Google Scholar
[7] Singer, , James, , “A Theorem in Finite Projective Geometry and Some Applications to Number Theory,” Trans. Amer. Math. Soc, vol. 43 (1938) 377–385.Google Scholar
[8] J. A., Todd, “A Combinatorial Problem,” J . of Math, and Physics, vol. 12 (1933), 321–333.Google Scholar
[9] Veblen, O. and Bussey, W. H., “Finite Projective Geometries,” Trans. Amer. Math. Soc, vol. 7 (1906), 241–259.Google Scholar
[10] van der Waerden, B. L., Moderne Algebra, I (Berlin, 1937), 165.Google Scholar