Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ferri, M.
Gagliardi, C.
and
Grasselli, L.
1986.
A graph-theoretical representation of PL-manifolds — A survey on crystallizations.
Aequationes Mathematicae,
Vol. 31,
Issue. 1,
p.
121.
Gagliardi, Carlo
1987.
On a class of 3-dimensional polyhedra.
ANNALI DELL UNIVERSITA DI FERRARA,
Vol. 33,
Issue. 1,
p.
51.
Lins, Sóstenes
1988.
On the Fundamental Group of 3-Gems and a ‘Planar’ Class of 3-manifolds.
European Journal of Combinatorics,
Vol. 9,
Issue. 4,
p.
291.
Lins, Sóstenes
1989.
Invariant Groups on Equivalent Crystallizations.
European Journal of Combinatorics,
Vol. 10,
Issue. 6,
p.
575.
Ferri, Massimo
and
Lins, Sóstenes
1991.
Topological aspects of edge fusions in 4-graphs.
Journal of Combinatorial Theory, Series B,
Vol. 51,
Issue. 2,
p.
227.
Kauffman, Louis
and
Lins, Sóstenes
1992.
Decomposition of the vertex group of 3-manifolds.
Discrete Mathematics,
Vol. 103,
Issue. 1,
p.
49.
Lins, Sóstenes
1997.
Twistors bridges among 3-manifolds.
Discrete Mathematics,
Vol. 177,
Issue. 1-3,
p.
145.
Carter, J.Scott
and
Lins, Sóstenes
1999.
Thin-G Theory and Local Moves for Gems.
Advances in Mathematics,
Vol. 143,
Issue. 2,
p.
251.
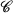 is the colour set, for each
is the colour set, for each 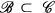 we set
we set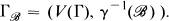
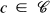 set
set 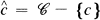 . For n ∊ Z, n ≧ 1, set
. For n ∊ Z, n ≧ 1, set