Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T10:54:18.995Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohomology Pairings on the Symplectic Reduction of Products

Published online by Cambridge University Press:  20 November 2018

R. F. Goldin  and
S. Martin
R. F. Goldin
Affiliation:
George Mason University, MS3 F2, 4400 University Drive, Fairfax, Virginia 22030, USA e-mail: [email protected] e-mail: [email protected]
S. Martin
Affiliation:
George Mason University, MS3 F2, 4400 University Drive, Fairfax, Virginia 22030, USA e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 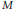$M$ be the product of two compact Hamiltonian 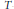$T$-spaces 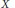$X$ and 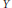$Y$. We present a formula for evaluating integrals on the symplectic reduction of 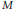$M$ by the diagonal 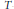$T$ action. At every regular value of the moment map for 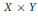$X\,\times \,Y$, the integral is the convolution of two distributions associated to the symplectic reductions of 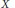$X$ by 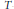$T$ and of 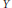$Y$ by 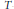$T$. Several examples illustrate the computational strength of this relationship. We also prove a linear analogue which can be used to find cohomology pairings on toric orbifolds.

Keywords

53D20
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 2 , 01 April 2006 , pp. 362 - 380
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Atiyah, M. F. and Bott, R., The moment map and equivariant cohomology. Topology 23(1984), 1–28.Google Scholar
[2] Berline, N. and Vergne, M., Classes caractéristiques équivariantes. Formule de localisation en cohomologie équivariante. C. R. Acad. Sci. Paris 295(1982), 539–541.Google Scholar
[3] Danilov, V. I. The geometry of toric varieties. Russian Math. Surveys 33(1978), 97–154.Google Scholar
[4] Duistermaat, J. J. and Heckman, G., On the variation of cohomology of the symplectic form of the reduced phase space. Invent.Math. (2) 69(1982), 259–268.Google Scholar
[5] Gelfand, I. M. and Shilov, , Generalized Functions, 1. New York, Academic Press, 1964.Google Scholar
[6] Ginzburg, V., Guillemin, V. and Karshon, Y., Cobordism theory and localization formulas for Hamiltonian group actions. Internat. Math. Res. Notices (5) (1996), 221–234.Google Scholar
[7] Ginzburg, V., Guillemin, V. and Karshon, Y., Moment Maps, Cobordisms, and Hamiltonian Group Actions. Amer.Math. Soc. (2002).Google Scholar
[8] Goldin, R., The cohomology ring of weight varieties and polygon spaces. Adv. in Math. (2) 160(2001), 175–204.Google Scholar
[9] Goldin, R., An effective algorithm for the cohomology ring of symplectic reductions. Geom. Funct. Anal. 12(2002), 567–583.Google Scholar
[10] Gromov, M., Pseudoholomorphic curves in symplectic manifolds. Invent.Math. 82(1985), 307–347.Google Scholar
[11] Guillemin, V., Reduced Phase Spaces and Riemann–Roch. Lie Theory and Geometry, Progr. Math. 123, Birkhäuser Boston, Boston, MA, 1994, 305–334.Google Scholar
[12] Guillemin, V. and Kalkman, J., The Jeffrey–Kirwan localization theorem and residue operations in equivariant cohomology. J. Reine Angew.Math. 470(1996), 123–142.Google Scholar
[13] Guillemin, V., Lerman, E. and Sternberg, S., Symplectic Fibrations and Multiplicity Diagrams. Cambridge University Press, 1996.Google Scholar
[14] Guillemin, V. and Sternberg, S., Birational equivalence in the symplectic category. Invent.Math. (3) 97(1989), 485–522.Google Scholar
[15] Guillemin, V. and Sternberg, S., The coefficients of the Duistermaat–Heckman polynomial and the cohomology ring of reduced spaces. Geometry, Topology and Physics, Conf. Proc. Lecture Notes Geom., Topology IV, Internat. Press, Cambridge, MA, 1995, 202–213.Google Scholar
[16] Jeffrey, L. and Kirwan, F., Localization for nonabelian group actions. Topology (2) 34(1995), 291–327.Google Scholar
[17] Jeffrey, L. and Kogan, M., Localization theorems for symplectic cuts. In: The Breadth of Symplectic and Poisson Geometry, Progr. Math. 232, Birkhäser, Boston, MA, 2005, pp. 303–326.Google Scholar
[18] Hausmann, J. C. and Knutson, A., The cohomology ring of polygon spaces. Ann. Inst. Fourier (Grenoble) (1) 48(1998), 281–321.Google Scholar
[19] Hsiang, Wu-Y., Cohomology theory of topological transformation groups. Springer-Verlag, New York, 1975.Google Scholar
[20] Kalkman, J., Cohomology rings of symplectic quotients. J. Reine Angew. Math. 458(1995), 37–52.Google Scholar
[21] Kirwan, F., Cohomology of Quotients in Symplectic and Algebraic Geometry. Princeton University Press, Princeton, NJ, 1984.Google Scholar
[22] Lerman, E., Symplectic Cuts. Math. Res. Lett. (3) 2(1995), 247–258.Google Scholar
[23] Martin, S., Transversality theory, cobordisms, and invariants of symplectic quotients. Ann. of Math. math. SG/0001001, to appear.Google Scholar
[24] Martin, S., Symplectic quotients by a nonabelian group and by its maximal torus. Ann. of Math. math. SG/0001002, to appear.Google Scholar
[25] Mohammadalikhani, R., Cohomology ring of symplectic quotients by circle actions. Canad. J. Math. (3) 56(2004), 553–565.Google Scholar
[26] Tolman, S. and Weitsman, J., The cohomology rings of symplectic quotients. Comm. Anal. Geom. (4) 11(2003), 751–773.Google Scholar
[27] Witten, E., Two-dimensional gravity and intersection theory on moduli space. Surveys in Differential Geometry, Cambridge, MA, 1990, Lehigh Univ., Bethlehem, PA, 1991, 243–310.Google Scholar