No CrossRef data available.
Article contents
Cobordism distance on the projective space of the knot concordance group
Published online by Cambridge University Press: 27 June 2023
Abstract
We use the cobordism distance on the smooth knot concordance group 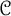 $\mathcal {C}$ to measure how close two knots are to being linearly dependent. Our measure,
$\mathcal {C}$ to measure how close two knots are to being linearly dependent. Our measure, 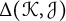 $\Delta (\mathcal {K}, \mathcal {J})$, is built by minimizing the cobordism distance between all pairs of knots,
$\Delta (\mathcal {K}, \mathcal {J})$, is built by minimizing the cobordism distance between all pairs of knots, 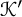 $\mathcal {K}'$ and
$\mathcal {K}'$ and 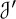 $\mathcal {J}'$, in cyclic subgroups containing
$\mathcal {J}'$, in cyclic subgroups containing 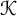 $\mathcal {K}$ and
$\mathcal {K}$ and 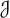 $\mathcal {J}$. When made precise, this leads to the definition of the projective space of the concordance group,
$\mathcal {J}$. When made precise, this leads to the definition of the projective space of the concordance group, 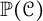 ${\mathbb P}(\mathcal {C})$, upon which
${\mathbb P}(\mathcal {C})$, upon which 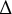 $\Delta $ defines an integer-valued metric. We explore basic properties of
$\Delta $ defines an integer-valued metric. We explore basic properties of 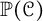 ${\mathbb P}(\mathcal {C})$ by using torus knots
${\mathbb P}(\mathcal {C})$ by using torus knots 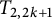 $T_{2,2k+1}$. Twist knots are used to demonstrate that the natural simplicial complex
$T_{2,2k+1}$. Twist knots are used to demonstrate that the natural simplicial complex 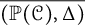 $\overline {({\mathbb P}(\mathcal {C}), \Delta )}$ associated with the metric space
$\overline {({\mathbb P}(\mathcal {C}), \Delta )}$ associated with the metric space 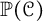 ${\mathbb P}(\mathcal {C})$ is infinite-dimensional.
${\mathbb P}(\mathcal {C})$ is infinite-dimensional.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
This work was supported by a grant from the National Science Foundation (Grant No. NSF-DMS-1505586).



