Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-23T11:58:14.566Z Has data issue: false hasContentIssue false
  • English
  • Français

Cluster Sets of Functions on an N-Ball

Published online by Cambridge University Press:  20 November 2018

P. T. Church
P. T. Church*
Affiliation:
Syracuse University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Dn be the open unit ball in En, and let Sn be the n-sphere. The cluster set C(f, p) of a function f : Dn —> Sn at a point p on the boundary of Dn is the set of points y in Sn such that there exists a sequence of points xm —> p, xm in Dn, with f(xm) —> y. Given an arc γ in 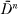, meeting the boundary bdy(Dn) only in p, the arc cluster set C(f, γ) is the set of points y in Sn such that there exists a sequence xm —> p, xm in γ, with f(xm) —> y.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 15 , 1963 , pp. 112 - 120
Copyright
Copyright © Canadian Mathematical Society 1963

References

1. Bers, L., On a theorem of Mori and the definition of quasi-conformality, Trans. Amer. Math . Soc, 84 (1957), 77–84.Google Scholar
2. Callender, E. D., Holder continuity of n-dimensional quasi-conformal mappings, Technical Report No. 81, Stanford University (1959).Google Scholar
3. Church, P. T., Extensions of Stoilow's theorem, J. London Math. Soc, 37 (1962), 86–89.Google Scholar
4. Gross, W., Uber die Singularitàten analytischer Funktionen, Monatsh. Math, und Phys., 29 (1918), 1–47.Google Scholar
5. Ince, E. L., Ordinary differential equations (New York, 1944).Google Scholar
6. Smale, S., A classification of immersions of the two-sphere, Trans. Amer. Math. Soc, 90 (1959), 281–290.Google Scholar
7. Weigand, L., Über die Randwerte meromorpher Funktionen einer Verdnderlichen, Comment. Math. Helv., 22, 2 (1949), 125–149.Google Scholar
8. Whyburn, G. T., Analytic topology (New York, 1942).Google Scholar