Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-18T12:48:03.410Z Has data issue: false hasContentIssue false
  • English
  • Français

Closed Ideals in Some Algebras of Analytic Functions

Published online by Cambridge University Press:  20 November 2018

Brahim Bouya
Brahim Bouya*
Affiliation:
Département de Mathématiques, Faculté des Sciences, Université Mohamed V, Rabat, Morocco, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We obtain a complete description of closed ideals of the algebra 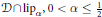$\mathcal{D}\cap \text{li}{{\text{p}}_{\alpha }},0<\alpha \le \frac{1}{2}$, where 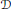$\mathcal{D}$ is the Dirichlet space and 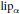$\text{li}{{\text{p}}_{\alpha }}$ is the algebra of analytic functions satisfying the Lipschitz condition of order $\alpha $.

Keywords

46E2030H0547A15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 2 , 01 April 2009 , pp. 282 - 298
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Carleson, L., A representation formula for the Dirichlet space. Math. Z. 73(1960), 190–196.Google Scholar
[2] El-Fallah, O., Kellay, K., and Ransford, T., Cyclicity in the Dirichlet space. Ark. Mat. 44(2006), no. 1, 61–86.Google Scholar
[3] Esterle, J., Strouse, E., and Zouakia, F., Closed ideals of A + and the Cantor set. J. Reine Angew. Math. 449(1994), 65–79.Google Scholar
[4] Hedenmalm, H. and Shields, A., Invariant subspaces in Banach spaces of analytic functions. Michigan Math. J. 37(1990), no. 1, 91–104.Google Scholar
[5] Hoffman, K., Banach spaces of analytic functions. Reprint of the 1962 original, Dover Publications Inc., New York, 1988.Google Scholar
[6] Korenbljuum, B. I., Invariant subspaces of the shift operator in a weighted Hilbert space. Mat. Sb. 89(131)(1972), 110–137, 166.Google Scholar
[7] Matheson, A., Approximation of analytic functions satisfying a Lipschitz condition. Michigan Math. J. 25(1978), no. 3, 289–298.Google Scholar
[8] Shamoyan, F. A., Closed ideals in algebras of functions that are analytic in the disk and smooth up to its boundary. Mat. Sb. 79(1994), no. 2, 425–445.Google Scholar
[9] Shirokov, N. A., Analytic functions smooth up to the boundary. Lecture notes in mathematics 1312, Springer-Verlag, Berlin, 1988.Google Scholar
[10] Shirokov, N. A., Closed ideals of algebras of type B α pq. Izv. Akad. Nauk. SSSR Ser. Mat. 46(1982), no. 6, 1316–1332, 1344.Google Scholar
[11] Taylor, B. A. and Williams, D. L., Ideals in rings of analytic functions with smooth boundary values. Canad J. Math. 22(1970), 1266–1283.Google Scholar