Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-18T12:53:11.786Z Has data issue: false hasContentIssue false
  • English
  • Français

Close Lattice Points on Circles

Published online by Cambridge University Press:  20 November 2018

Javier Cilleruelo  and
Andrew Granville
Javier Cilleruelo
Affiliation:
Instituto de Ciencias Matemáticas (CSIC-UAM-UC3M-UCM) and Departamento de Matemáticas, Universidad Autónoma de Madrid, 28049 Madrid, Spain email: [email protected]
Andrew Granville
Affiliation:
Départment de Mathématiques et Statistique, Université de Montréal, CP 6128 succ Centre-Ville, Montréal, QC H3C 3J7 email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We classify the sets of four lattice points that all lie on a short arc of a circle that has its center at the origin; specifically on arcs of length 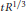$t{{R}^{1/3}}$ on a circle of radius 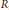$R$, for any given 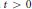$t\,>\,0$. In particular we prove that any arc of length 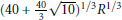${{\left( 40\,+\frac{40}{3}\sqrt{10} \right)}^{1/3}}\,{{R}^{1/3}}$ on a circle of radius 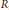$R$, with 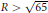$R\,>\,\sqrt{65}$, contains at most three lattice points, whereas we give an explicit infinite family of 4-tuples of lattice points, 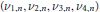$\left( {{v}_{1,n}},\,{{v}_{2,n}},\,{{v}_{3,n}},\,{{v}_{4,n}} \right)$, each of which lies on an arc of length 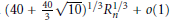${{\left( 40+\frac{40}{3}\sqrt{10} \right)}^{1/3}}R_{n}^{1/3}\,+\,o\left( 1 \right)$ on a circle of radius 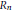${{R}_{n}}$.

Keywords

11N36
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 6 , 01 December 2009 , pp. 1214 - 1238
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Bombieri, E. and Pila, J., The number of integral points on arcs and ovals. Duke Math. J. 59(1989), 337–357.Google Scholar
[2] Cilleruelo, J., Arcs containing no three lattice points. Acta Arithmetica 59(1991), 87–90.Google Scholar
[3] Cilleruelo, J. and Córdoba, A., Trigonometric polynomials and lattice points. Proc. Amer. Math. Soc. 115(1992), 899–905.Google Scholar
[4] Cilleruelo, J. and Granville, A., Lattice points on circles, squares in arithmetic progressions and sumset of squares. In: Additive Combinatorics, CR MProc. Lecture Notes 43, American Mathematical Society, Providence, RI, 2007, pp. 241–262.Google Scholar
[5] Cilleruelo, J. and Granville, A., Close divisors. In preparation. www.dms.umontreal.ca/∼andrew/preprints.html Google Scholar
[6] Cilleruelo, J. and Tenenbaum, G., An overlapping theorem with applications. Publicacions Mathematiques, 51(2007), 107–118.Google Scholar
[7] Elkies, N. D., Rational points near curves and small nonzero |x 3 − y2| via lattice reduction. In: Algorithmic Number Theory, Lecture Notes in Comput. Sci. 1838 Springer-Verlag, New York 2000, pp. 33–63.Google Scholar
[8] Ellenberg, J. and Venkatesh, A., On uniform bounds for rational points on nonrational curves. Int. Math. Res. Not. 35(2005), 2163–2181.Google Scholar
[9] Heath-Brown, R., The density of rational points on curves and surfaces. Ann. of Math. 155(2002), 553–595.Google Scholar
[10] Zygmund, A., A Cantor-Lebesgue theorem for double trigonometric series. Studia Matematica 43(1972), 173–178.Google Scholar