Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-17T15:35:39.586Z Has data issue: false hasContentIssue false
  • English
  • Français

Classifying spaces for étale algebras with generators

Part of: (Co)homology theory Fiber spaces and bundles Chain conditions, finiteness conditions

Published online by Cambridge University Press:  30 March 2020

Abhishek Kumar Shukla  and
Ben Williams
Abhishek Kumar Shukla
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BCV6T 1Z2, Canada e-mail: [email protected]
Ben Williams*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BCV6T 1Z2, Canada e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct a scheme 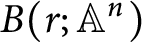$B(r; {\mathbb {A}}^n)$ such that a map 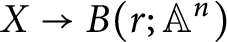$X \to B(r; {\mathbb {A}}^n)$ corresponds to a degree-n étale algebra on X equipped with r generating global sections. We then show that when 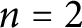$n=2$ , i.e., in the quadratic étale case, the singular cohomology of 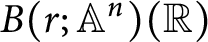$B(r; {\mathbb {A}}^n)({\mathbb {R}})$ can be used to reconstruct a famous example of S. Chase and to extend its application to showing that there is a smooth affine 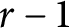$r-1$ -dimensional 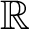${\mathbb {R}}$ -variety on which there are étale algebras 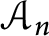${\mathcal {A}}_n$ of arbitrary degrees n that cannot be generated by fewer than r elements. This shows that in the étale algebra case, a bound established by U. First and Z. Reichstein in [6] is sharp.

Keywords

Étale algebrasalgebra generatorsclassifying spaces

MSC classification

Primary: 13E15: Rings and modules of finite generation or presentation; number of generators
Secondary: 14F25: Classical real and complex (co)homology 14F42: Motivic cohomology; motivic homotopy theory 55R40: Homology of classifying spaces, characteristic classes
Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 3 , June 2021 , pp. 854 - 874
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was partially supported by a graduate fellowship from the Science and Engineering Research Board, India. The second author was partially supported by an NSERC discovery grant.

References

Atiyah, M. F. and Macdonald, I. G., Introduction to commutative algebra. Addison Wesley Series in Mathematics, Addison-Wesley Pub. Co., Reading, MA, 1969.Google Scholar
de Jong, A. J., Stacks Project, January 2017. http://stacks.math.columbia.edu/.Google Scholar
Dold, A., Partitions of unity in the theory of fibrations. Ann. Math. 78(1963), 223–255. http://dx.doi.org/10.2307/1970341 CrossRefGoogle Scholar
Dugger, D. and Isaksen, D. C., The Hopf condition for bilinear forms over arbitrary fields. Ann. of Math. (2) 165(2007), 943–964. http://dx.doi.org/10.4007/annals.2007.165.943 CrossRefGoogle Scholar
Eisenbud, D. and Harris, J., The geometry of schemes. Graduate Texts in Mathematics, 197, New York, 2000. http://dx.doi.org/10.1007/b97680 Google Scholar
First, U. A. and Reichstein, Z., On the number of generators of an algebra. C. R. Math. Acad. Sci. Paris 355(2017), 5–9. http://dx.doi.org/10.1016/j.crma.2016.11.015 CrossRefGoogle Scholar
Ford, T. J., Separable algebras. Graduate Studies in Mathematics, 183, Amer. Math. Soc., Providence, RI, 2017. http://dx.doi.org/10.1090/gsm/183 CrossRefGoogle Scholar
Forster, O., Über die Anzahl der Erzeugenden eines Ideals in einem Noetherschen Ring. Math. Z. 84(1964), 80–87. http://dx.doi.org/10.1007/BF01112211 CrossRefGoogle Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV. Inst. Hautes Études Sci. Publ. Math. 32(1967), 361.Google Scholar
Grothendieck, A., Revêtements étales et groupe fondamental. Fasc. I: Exposés 1 à 5. Séminaire de Géométrie Algébrique, 1960/61, Institut des Hautes Études Scientifiques, Paris, 1963.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. I. Inst. Hautes Études Sci. Publ. Math. 20(1964), 259.Google Scholar
Hatcher, A., Algebraic topology. Cambridge University Press, Cambridge, 2002.Google Scholar
Karpenko, N. A. and Merkurjev, A. S., Chow groups of projective quadrics. Algebra i Analiz 2(1990), 218–235.Google Scholar
Knus, M.-A., Quadratic and Hermitian forms over rings. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 294, Springer-Verlag, Berlin, 1991. With a foreword by I. Bertuccioni. http://dx.doi.org/10.1007/978-3-642-75401-2 Google Scholar
Liu, Q. and Erne, R., Algebraic geometry and arithmetic curves. Oxford University, Oxford, 2002.Google Scholar
Mazza, C., Voevodsky, V., and Weibel, C., Lecture notes on motivic cohomology. Clay Mathematics Monographs, 2, Amer. Math. Soc., Providence, RI, 2006.Google Scholar
Milne, J. S., Étale cohomology. Princeton Mathematical Series, 33, Princeton University Press, Princeton, NJ, 1980.Google Scholar
Morel, F. and Voevodsky, V., ${A}^{1}$ -homotopy theory of schemes. Inst. Hautes Études Sci. Publ. Math. 90(2001), 45–143. http://www.numdam.org/item?id=PMIHES_1999__90__45_0. http://dx.doi.org/10.1007/bf02698831 CrossRefGoogle Scholar
Pavaman Murthy, M., Zero cycles and projective modules. Ann. of Math. (2) 140(1994), 405–434. http://dx.doi.org/10.2307/2118605 CrossRefGoogle Scholar
Swan, R. G., The nontriviality of the restriction map in the cohomology of groups. Proc. Am. Math. Soc. 11(1960), 885–887. http://dx.doi.org/10.2307/2034431 Google Scholar
Swan, R. G., The number of generators of a module. Math. Z. 102(1967), 318–322. http://dx.doi.org/10.1007/BF01110912 CrossRefGoogle Scholar
Totaro, B., The Chow ring of a classifying space. Algebraic $K$ -theory (Seattle, WA, 1997). Proc. Sympos. Pure Math., 67, Amer. Math. Soc., Providence, RI, 1999, pp. 249–281. http://dx.doi.org/10.1090/pspum/067/1743244 Google Scholar
Voevodsky, V., Reduced power operations in motivic cohomology. Publ. Math. Inst. Hautes Études Sci. 98(2003), 1–57. http://dx.doi.org/10.1007/s10240-003-0009-z CrossRefGoogle Scholar