Article contents
Chern Characters of Fourier Modules
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 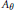 ${{A}_{\theta}}$ denote the rotation algebra—the universal
${{A}_{\theta}}$ denote the rotation algebra—the universal 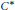 ${{C}^{*}}$-algebra generated by unitaries
${{C}^{*}}$-algebra generated by unitaries 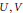 $U,V$ satisfying
$U,V$ satisfying 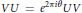 $VU={{e}^{2\pi i\theta }}UV$, where
$VU={{e}^{2\pi i\theta }}UV$, where  $\theta $ is a fixed real number. Let
$\theta $ is a fixed real number. Let  $\sigma $ denote the Fourier automorphism of
$\sigma $ denote the Fourier automorphism of 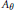 ${{A}_{\theta}}$ defined by
${{A}_{\theta}}$ defined by 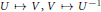 $U\mapsto V\text{,}V\mapsto {{U}^{-1}}$, and let
$U\mapsto V\text{,}V\mapsto {{U}^{-1}}$, and let 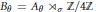 ${{B}_{\theta }}={{A}_{\theta }}{{\rtimes }_{\sigma }}\mathbb{Z}/4\mathbb{Z}$ denote the associated
${{B}_{\theta }}={{A}_{\theta }}{{\rtimes }_{\sigma }}\mathbb{Z}/4\mathbb{Z}$ denote the associated 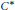 ${{C}^{*}}$-crossed product. It is shown that there is a canonical inclusion
${{C}^{*}}$-crossed product. It is shown that there is a canonical inclusion 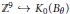 ${{\mathbb{Z}}^{9}}\hookrightarrow {{K}_{0}}({{B}_{\theta }})$ for each
${{\mathbb{Z}}^{9}}\hookrightarrow {{K}_{0}}({{B}_{\theta }})$ for each  $\theta $ given by nine canonical modules. The unbounded trace functionals of
$\theta $ given by nine canonical modules. The unbounded trace functionals of 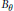 ${{B}_{\theta }}$ (yielding the Chern characters here) are calculated to obtain the cyclic cohomology group of order zero
${{B}_{\theta }}$ (yielding the Chern characters here) are calculated to obtain the cyclic cohomology group of order zero 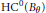 $\text{H}{{\text{C}}^{0}}({{B}_{\theta }})$ when
$\text{H}{{\text{C}}^{0}}({{B}_{\theta }})$ when  $\theta $ is irrational. The Chern characters of the nine modules—and more importantly, the Fourier module—are computed and shown to involve techniques from the theory of Jacobi’s theta functions. Also derived are explicit equations connecting unbounded traces across strong Morita equivalence, which turn out to be non-commutative extensions of certain theta function equations. These results provide the basis for showing that for a dense
$\theta $ is irrational. The Chern characters of the nine modules—and more importantly, the Fourier module—are computed and shown to involve techniques from the theory of Jacobi’s theta functions. Also derived are explicit equations connecting unbounded traces across strong Morita equivalence, which turn out to be non-commutative extensions of certain theta function equations. These results provide the basis for showing that for a dense 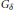 ${{\text{G}}_{\delta }}$ set of values of
${{\text{G}}_{\delta }}$ set of values of  $\theta $ one has
$\theta $ one has 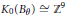 ${{K}_{0}}({{B}_{\theta }})\cong {{\mathbb{Z}}^{9}}$ and is generated by the nine classes constructed here.
${{K}_{0}}({{B}_{\theta }})\cong {{\mathbb{Z}}^{9}}$ and is generated by the nine classes constructed here.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2000
References
- 10
- Cited by


