Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-03T20:30:19.808Z Has data issue: false hasContentIssue false
  • English
  • Français

A Characterization of Some Geometries of Chains

Published online by Cambridge University Press:  20 November 2018

Yi Chen
Yi Chen*
Affiliation:
University of Waterloo, Waterloo, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The geometries considered here are the Möbius plane M(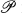) (W. Benz [1]), the Laguerre plane L(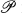) (W. Benz and H. Mäurer [7]) and the Minkowski plane A(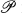) (W. Benz [5], G. Kaerlein [18]) over a field 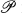. All of them are geometries of an algebra with identity over a field.

The characterization of the projective plane over a field by the proposition of Pappus first gave a close relation between algebraic and geometric structures. B. L. v. d. Waedern and L. J. Smid [28] presented a further example by characterizing the Möbius and Laguerre plane with incidence axioms and the "complete" proposition of Miquel.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 2 , April 1974 , pp. 257 - 272
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Benz, W., Axiomatischer Aufbau der Kreisgéométrie auf Grund von Doppelverhàltnissen, J. Reine Angew. 199 (1958), 56–90.Google Scholar
2. Benz, W., Zür Möbiusgéométrie über einem Körperpaar, Arch. Math. 8 (1962), 136–146.Google Scholar
3. Benz, W., Über Winkel-und Transitivitdtseigenschaften in den Kreisebenen, I, II, J. Reine. Angew. Math. 205 (1960), 48–74; 206 (1961), 1–15.Google Scholar
4. Benz, W., Eine Kennzeichnung der van der Waerden-Smid-Geometrien, Math. Ann. 165 (1966), 19–23.Google Scholar
5. Benz, W., Über die Grundlagen der Geometrie der Kreise in der pseudoeuclidischen (Minkowskischen) Géométrie, J. Reine, Angew. Math. 232 (1968), 41–76.Google Scholar
6. Benz, W., Suss'sche Gruppen in affinen Ebenen mit Nachbarelementen and allgemeinersen Strukturen, Abh. Math. Sem. Univ. Hamburg 26 (1963), 83–101.Google Scholar
7. Benz, W. and Mäurer, H., Uber die Grundlagen der Laguerre-Geometrie, Ein Bericht. J.-Ber. Deutsch. Math. Verein. 67 (1964), 14–42.Google Scholar
8. Chen, Y., Der Satz von Miquel in der Möbiusebene, Math. Ann. 186 (1970), 81–100.Google Scholar
9. Chen, Y., A characterization of the pseudo-Euclidean circle-geometry, Abh. Math. Sem. Univ. Hamburg 40 (1973), 31–42.Google Scholar
10. Chen, Y., Cross ratio in the geometry over an algebra (to appear).Google Scholar
11. Chen, Y., Angle in the geometry of chains (to appear).Google Scholar
12. Chen, Y. and Kaerlein, G., Eine Bemerkung über endliche Laguerre-und Minkowski-Ebenen, Geometriae Dedicata 2/2 (1973), 193–194.Google Scholar
13. Dembowski, P., Finite geometries (Springer, Berlin, Heidelberg, New York, 1970).Google Scholar
14. Ewald, G., Axiomatischer Aufbau der Kreis géométrie, Math. Ann. 131 (1956), 354–371.Google Scholar
15. Ewald, G., Uber den Begriff der Orthogonalitdt in der Kreis géométrie, Math. Ann. 131 (1956), 463–469.Google Scholar
16. Hoffmann, A. J., Chains in the projective line, Duke Math. J. 18 (1951), 827–830.Google Scholar
17. Hoffmann, A. J., On the foundation of inversion geometry, Trans. Amer. Math. Soc. 71 (1951), 218–242.Google Scholar
18. Kaerlein, G., Der Satz von Miquel in der pseudo-euklidischen (Minkowskishen) Géométrie, Ph.D. Thesis, Bochum, 1970.Google Scholar
19. Klingeberg, W., Projective und Affine Ebenen mit Nachbarelementen, Math. Z. 61 (1954), 1–25.Google Scholar
20. Mâurer, H., Ein Spiegelungs geometrischer Aufbau der Laguerre-Geometrie. I, II. Math. Z. 87 (1965), 78–100; 263-282.Google Scholar
21. Melchior, U., Die projektive Gerade Uber einem lokalen Ring. Ihre lineare Gruppe und ihre Géométrie, Ph.D. Thesis, Bochum, 1968.Google Scholar
22. Peczar, L., Über eine einheitliche Méthode zum Beweis gewisser Schliessungssàtze, Mh. Math. 54 (1950), 210–220.Google Scholar
23. Petkantschin, B., Axiomatischer Aufbau der zweidimenionalen Möbiusschen Geometric Annuaire Univ. Sofia II, Fac. Phys.-Math 1 (1940), 219–235.Google Scholar
24. Pickert, G., Der Satz von Pappos mit Festelementen, Arch. Math. 10 (1959), 56–61.Google Scholar
25. Smid, L. J., Over Circeltneetkunden, Ph.D. Thesis, Groningen, 1928.Google Scholar
26. Siïss, W., Beitràge zur gruppen theoretischen Bergrùndung der Géométrie. II, III, Tôhoku Math. J. 27 (1926), 213–242; 28 (1927), 228–241.Google Scholar
27. Uhl, A., Ein axiomatischer Aufbau der Laguerre-Geometrie, Ph.D. Thesis, Karlsruhe, 1964.Google Scholar
28. Waerden, B. L. v. d. and Smid, L. J., Eine Axiomatik der Kreisgéométrie und der Laguerre géométrie, Math. Ann. 110 (1935), 753–776.Google Scholar