Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T04:46:33.185Z Has data issue: false hasContentIssue false
  • English
  • Français

A Characterization of Sharply Transferable Lattices

Published online by Cambridge University Press:  20 November 2018

G. Grätzer  and
C. R. Platt
G. Grätzer
Affiliation:
University of Manitoba, Winnipeg, Manitoba
C. R. Platt
Affiliation:
University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A lattice L is called transferable if and only if, whenever L can be embedded in the ideal lattice I(K) of a lattice K, L can be embedded in K. L is called sharply transferable if and only if, for every lattice embedding ψ(x) , there exists an embedding 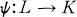such that for x, y ϵ L, 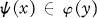if and only if x ≤ y. Finite sharply transferable lattices were characterized in [3]. In this paper we extend the characterization to the infinite case. We begin by revising some of the terminology of [3].

1.1. Definition, (a) Let 〈P; ≧〉 be a poset and X, Y ⊆ P. Then X dominates Y (written X Dom Y) if and only if, for every y ∈ F, there exists x ∈ X such that y ∈ x. Dually, X supports Y (written X Spp Y) if and only if, for every y ∈ Y, there exists x ∈ X such that x ≦ y.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 1 , 01 February 1980 , pp. 145 - 154
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Antonius, R. and Rival, I., A note on Whitman's property for free lattices, Algebra Universali. 4 (1974), 271–272.Google Scholar
2. Freese, R. and Nation, J. B., Projective lattices, Manuscript.Google Scholar
3. Gaskill, H. S., Grätzer, G., and Piatt, C. R., Sharply transferable lattices, Can. J. Math. 27 (1975), 1246–1262.Google Scholar
4. Gràtzer, G., General lattice theory (Birkhäuser Verlag, Basel ; Academic Press, New York, 1978).Google Scholar
5. Gràtzer, G. and Piatt, C. R., Two embeddiwg theorems for lattices, Proc. Amer. Math. Soc. 69 (1978), 21–24.Google Scholar
6. Jônsson, B. and Nation, J. B., A report on sublattices of a free lattice, Universal Algebra (Proc. Colloq. Szeged, 1975), Colloq. Math. Soc. Jänos Bôlya. 17 (1977), 223–257.Google Scholar
7. Lakser, H., Finite projective lattices are sharply transferable, Algebra Universali. 5 (1975), 407–409.Google Scholar
8. Whitman, Ph. M., Lattices, equivalence relations, and subgroups, Bull. Amer. Math. Soc. 52 (1946), 507–522.Google Scholar