Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-01T04:53:00.973Z Has data issue: false hasContentIssue false
  • English
  • Français

A Characterization of PSL(2, 31) and its Geometry

Published online by Cambridge University Press:  20 November 2018

Manley Perkel
Manley Perkel*
Affiliation:
Wright State University, Dayton, Ohio
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The aim of this paper is the characterization of PSL(2, 31) in terms of its action on a certain polygonal graph. A polygonal graph is a pair (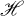, ) consisting of a graph 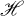which is regular, connected and has girth m for some m ≧ 3, and a set of m-gons (circuits of length m) of 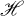such that every 2-claw (i.e. path of length 2) of 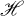is contained in a unique element of , (See Section 2 for the definitions of the terms used here.) If is the set of all m-gons of H, so that there is in 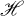a unique m-gon on every one of its 2-claws, then we write 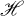for (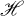, ) and call 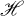a strict polygonal graph. If we wish to emphasize the integer m, then we call (, ) an m-gon-graph (respectively, a strict m-gon-graph). For convenience, a strict 5-gon-graph will be called a pentagraph.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 1 , 01 February 1980 , pp. 155 - 164
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Coxeter, H. S. M. and Moser, W. O. J., Generators and relations for discrete, groups (Third edition, Springer, Berlin, 1972).Google Scholar
2. Higman, D. G., Finite permutation groups of rank 3, Math. Z. 86 (1964). 145–156.Google Scholar
3. Huppert, B., Endliche Gruppen I, Grundlehren der math. Wissenschaften 134 (Springer, Berlin, 1968).Google Scholar
4. Perkel, M., Bounding the valency of polygonal graphs with odd girth, to appear in Can. J. Math.Google Scholar
5. Scott, R., Coset enumeration program, University of Michigan, Ann Arbor, Mich., private communication.Google Scholar