Published online by Cambridge University Press: 20 November 2018
Let 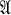 be an associative algebra over the field
be an associative algebra over the field 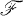 and let
and let 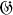 be the group of all automorphisms and anti-automorphisms of
be the group of all automorphisms and anti-automorphisms of 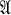 which leave
which leave 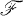 elementwise invariant. A function Fwith domain
elementwise invariant. A function Fwith domain 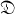 and range contained in
and range contained in 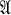 is called an intrinsic functionon
is called an intrinsic functionon 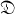 if (i)
if (i) 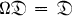 for each Ω in
for each Ω in 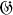 and (ii) F(ΩZ) = ΩF(Z) for every Z in
and (ii) F(ΩZ) = ΩF(Z) for every Z in 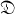 .
.
Rinehart (5) has introduced and motivated the study of the class of intrinsic functions on 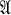 , and has characterized these functions for the cases in which
, and has characterized these functions for the cases in which 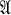 is the algebra
is the algebra 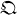 of real quaternions, the algebra
of real quaternions, the algebra 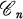 of n × ncomplex matrices, or the algebra
of n × ncomplex matrices, or the algebra 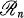 of n× nreal matrices (5; 6). The algebras listed above, along with the algebra
of n× nreal matrices (5; 6). The algebras listed above, along with the algebra  of n × nquaternion matrices, constitute the full list of possibilities for the simple direct summands of any semi-simple algebra over
of n × nquaternion matrices, constitute the full list of possibilities for the simple direct summands of any semi-simple algebra over 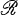 or
or 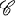 ; see (2).
; see (2).